Другие числовые характеристики

Мода дискретной СВ X определяется как такое возможное значение x_m, для которого

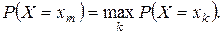(1.25)

Модой непрерывной СВ X называется действительное число M₀(X), определяемое как точка максимума плотности распределения вероятностей f(x).

Таким образом, мода СВ X есть ее наиболее вероятное значение, если такое значение единственно. Мода может не существовать, иметь единственное значение (унимодальное распределение) или иметь несколько значений (мультимодальное распределение).

Медианой непрерывной СВ X называется действительное число M_D(X), удовлетворяющее условию

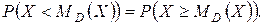(1.26)

Так как данное уравнение может иметь множество корней, то медиана определяется, вообще говоря, неоднозначно.

Начальным моментом m-го порядка СВ X (если он существует) называется действительное число a_m, определяемое по формуле

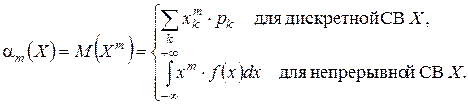(1.27)

Центральным моментом m-го порядка СВ X (если он существует) называется число m_m, определяемое по формуле

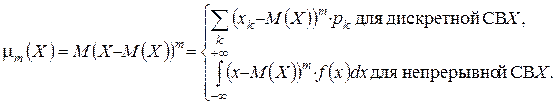(1.28)

Математическое ожидание СВ X есть ее первый начальный момент, а дисперсия – второй центральный.

Среди моментов высших порядков особое значение имеют центральные моменты 3-го и 4-го порядков.

Коэффициентом асимметрии ("скошенности") А(X) называется величина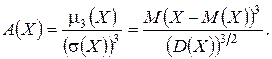

Коэффициентом эксцесса ("островершинности") E(X) СВ X называется величина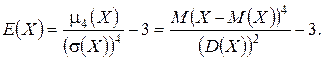

Некоторые законы распределения дискретных случайных величин

Геометрическое распределение

Дискретная СВ X имеет геометрическое распределение, если ее возможным значениям 0, 1, 2, …, m, … соответствуют вероятности, вычисляемые по формуле

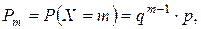(1.29)

где 0 < p < 1, q = 1 – p.

На практике геометрическое распределение встречается, когда производится ряд независимых попыток достигнуть какого-то результата А и вероятность появления события А в каждой попытке P(A) = P. СВ X – число бесполезных попыток (до первого опыта, в котором появится событие А), имеет геометрическое распределение с рядом распределения:

xi				…	m	…
pi	p	qp	q2p	...	qmp	…

и числовыми характеристиками:

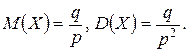(1.30)

Гипергеометрическое распределение

Дискретная СВ X с возможными значениями 0, 1, …, m, …, M имеет гипергеометрическое распределение с параметрами N, M, n, если

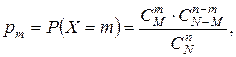(1.31)

где M ≤ N, m ≤ n, n ≤ N, m, n, N, M – натуральные числа.

Гипергеометрическое распределение возникает в случаях, подобных следующему: имеется N объектов, из которых M обладают определенным признаком. Из имеющихся N объектов наудачу выбираются n объектов.

СВ X – число объектов с указанным признаком среди выбираемых, распределена по гипергеометрическому закону.

Гипергеометрическое распределение используется, в частности, при решении задач, связанных с контролем качества продукции.

Математическое ожидание случайной величины, имеющей гипергеометрическое распределение, равно:

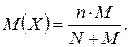(1.32)

Биномиальное распределение

Дискретная СВ X распределена по биномиальному закону, если она принимает значения 0, 1, 2, …, n с вероятностями:

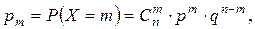(1.33)

где 0 < p < 1, q = 1 – p, m = 0, 1, …, n.

Из схемы Бернулли следует, что СВ X – число появлений события А в серии из n независимых опытов, в каждом из которых событие А может появиться с вероятностью p, имеет биномиальное распределение. Для
СВ X, имеющей биномиальное распределение с параметрами p и n,

M(X) = np, D(X) = npq, (1.34)

где q = 1 – p.

Следует отметить, что гипергеометрическое распределение при n малых по сравнению с N (практически при n < 0,1N) приближается к биномиальному распределению с параметрами n и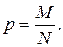

Замечание 1. Для вычисления 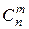при достаточно больших n и m применима формула Стирлинга:

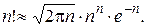
Замечание 2. Для биномиальных вероятностей справедлива рекуррентная формула:

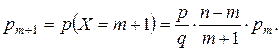
Замечание 3. Наиболее вероятное число успехов K₀ в серии из n независимых испытаний удовлетворяет неравенству:

np – q ≤ K₀ < np + p.

Предельные теоремы

При большом числе испытаний непосредственное вычисление вероятностей P(X = m) и P(m₁ ≤ X ≤ m₂) для СВ X, распределено по биномиальному закону, становится громоздким, так как факториалы, входящие в формулу 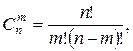будут очень большими числами. В этом случае для вычисления указанных вероятностей можно использовать асимптотические (предельные) формулы.

Когда оба параметра p и q заметно отличны от 0, применяются локальная (1.35, 1.36) и интегральная формулы Муавра-Лапласа (1.38, 1.40).

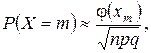(1.35)

где

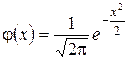(1.36)

– плотность нормированной нормальной СВ X, а

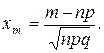(1.37)

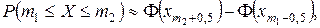(1.38)

где

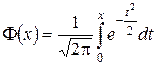(1.39)

– функция Лапласа,

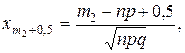
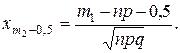(1.40)

Имеются таблицы значений j(x) (таблица 1) и F(x) (npq > 20) (таблица 2).

С помощью этих формул при n ³ 100 и npq > 20, как правило, удается получить искомые вероятности с точностью до трех-четырех знаков после запятой.

Распределение Пуассона

Дискретная СВ X называется распределенной по закону Пуассона, если ее возможные значения 0, 1, 2, …, m, …, а вероятность события (X = m) выражается формулой

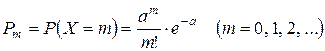, (1.41)

где a > 0. Распределение Пуассона зависит от одного параметра а. Для СВ X, распределенной по закону Пуассона,

M(X) = D(X) = a, (1.42)

т. е. параметр a пуассоновского распределения равен одновременно M(X) и D(X). В этом состоит отличительная особенность распределения Пуассона, которая используется на практике (на основании опытных данных находят оценки для M(X) и D(X); если они близки между собой, то есть основание считать, что СВ X распределена по закону Пуассона).

Пуассоновское распределение является предельным для биномиального при p ® 0, n ® ¥, если np = a = const. Этим распределением можно пользоваться приближенно, если производится большое число независимых опытов, в каждом из которых событие A происходит с малой вероятностью. Примерами СВ X, имеющих распределение Пуассона, являются: число опечаток в большом тексте, число бракованных деталей в большой партии; число a-частиц, испускаемых радиоактивным источником и т. д. При этом считается, что события появляются независимо друг от друга с постоянной интенсивностью, характеризующейся параметром a = np.

Замечание. Имеются специальные таблицы, пользуясь которыми можно найти P_m, зная m и a.

Распределение Пуассона встречается при рассмотрении потоков событий. Потоком событий называется последовательность однородных событий, наступающих одно за другим в случайные моменты времени.

Среднее число событий l, приходящееся на единицу времени, называется интенсивностью потока. Величина l может быть как постоянной, так и переменной l = l(t).

Поток событий называется потоком без последействия, если вероятность попадания того или иного числа событий на какой-либо участок времени не зависит от того, сколько событий попало на любой другой непересекающийся с ним участок.

Поток событий называется ординарным, если вероятность появления на элементарном участке времени Dt двух или более событий пренебрежимо мала по сравнению с вероятностью появления одного события. Ординарный поток событий без последствия называется пуассоновским. Если события образуют пуассоновский поток, то число X событий, попадающих на любой участок времени (t₀, t₀ + t), распределено по закону Пуассона:

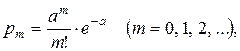
где a – математическое ожидание числа событий, попадающих на участок:

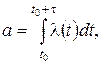
где l(t) – интенсивность потока.

Если l = const, то пуассоновский поток называется стационарным пуассоновским или простейшим. Для простейшего потока число событий, попадающих на любой участок времени длины t, распределено по закону Пуассона с параметром а = l × t.

В качестве примеров потоков можно рассматривать поступления вызовов на АТС, на пункт неотложной медицинской помощи, прибытие самолетов в аэропорт, клиентов на предприятие бытового обслуживания, последовательность отказов элементов некоторого устройства.