Основные формулы комбинаторики. Вероятность событий. Свойства Вероятностей. Геометрические вероятности.

При вычислении вероятностей часто приходится использовать некоторые формулы комбинаторики – науки, изучающей комбинации, которые можно составить по определенным правилам из элементов некоторого конечного множества. Определим основные такие комбинации.

1. Перестановки– это комбинации, составленные из всех п элементов данного множества и отличающиеся только порядком их расположения. Число всех возможных перестановок Р_п = п!

2.Размещения – комбинации из т элементов множества, содержащего п различных элементов, отличающиеся либо составом элементов, либо их порядком. Число всех возможных размещений

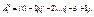
3.Сочетания – неупорядоченные наборы из т элементов множества, содержащего п различных элементов (то есть наборы, отличающиеся только составом элементов). Число сочетаний

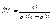
Вероятность событий

При изучении случайных событий возникает необходимость количественно сравнивать возможность их появления в результате опыта. Например, при последовательном извлечении из колоды пяти карт более возможна ситуация, когда появились карты разных мастей, чем появление пяти карт одной масти; при десяти бросках монеты более возможно чередование гербов и цифр, нежели выпадение подряд десяти гербов, и т.д. Поэтому с каждым таким событием связывают по определенному правилу некоторое число, которое тем больше, чем более возможно событие. Это число называется вероятностью события и является вторым основным понятием теории вероятностей.

Отметим, что само понятие вероятности, как и понятие случайного события, является аксиоматическим и поэтому не поддается строгому определению. То, что в дальнейшем будет называться различными определениями вероятности, представляет собой способы вычисления этой величины.

Если все события, которые могут произойти в результате данного опыта,

а) попарно несовместны;

б) равновозможны;

в) образуют полную группу,

то говорят, что имеет место схема случаев.

Можно считать, что случаи представляют собой все множество исходов опыта. Пусть их число равно п ( число возможных исходов), а при т из них происходит некоторое событие А (число благоприятных исходов).

Вероятностью события Аназывается отношение числа исходов опыта, благоприятных этому событию, к числу возможных исходов:

- классическое определение вероятности.

Свойства вероятности.

Из определения 1.8 вытекают следующие свойства вероятности:

1. Вероятность достоверного события равна единице.

Доказательство. Так как достоверное событие всегда происходит в результате опыта, то все исходы этого опыта являются для него благоприятными, то есть т = п, следовательно,

Р(А) = 1.

2. Вероятность невозможного события равна нулю.

Доказательство. Для невозможного события ни один исход опыта не является благопри-ятным, поэтому т = 0 и р(А) = 0.

3. Вероятность случайного события есть положительное число, заключенное между нулем и единицей.

Доказательство. Случайное событие происходит при некоторых исходах опыта, но не при всех, следовательно, 0 < m < n, и из (1.1) следует, что 0 < p(A) < 1.

Геометрическая вероятность

Одним из недостатков классического определения вероятности является то, что оно неприменимо к испытаниям с бесконечным количеством исходов. В таких случаях можно воспользоваться понятием геометрической вероятности.

Пусть на отрезок L наудачу брошена точка. Это означает, что точка обязательно попадет на отрезок L и с равной возможностью может совпасть с любой точкой этого отрезка. При этом вероятность попадания точки на любую часть отрезка L не зависит от расположения этой части на отрезке и пропорциональна его длине. Тогда вероятность того, что брошен-ная точка попадет на отрезок l, являющийся частью отрезка L, вычисляется по формуле:

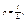(2.1)

где l – длина отрезка l, а L – длина отрезка L.Можно дать аналогичную постановку задачи для точки, брошенной на плоскую область S и вероятности того, что она попадет на часть этой области s:

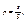(2.1`)

где s – площадь части области, а S – площадь всей области.

В трехмерном случае вероятность того, что точка, случайным образом расположенная в теле V, попадет в его часть v, задается формулой:

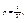(2.1``)

где v – объем части тела, а V – объем всего тела.

3.Теоремы теории вероятностей. Теорема сложения вероятностей несовместимых событий. Полная группа событий. Противоположные события.

Теорема1. (теорема сложения).Вероятность р(А + В) суммы событий А и В равна

Р (А + В ) = р (А) + р (В) – р (АВ). (2.2)

Доказательство.

Докажем теорему сложения для схемы случаев. Пусть п – число возможных исходов опыта, т_А – число исходов, благоприятных событию А, т_В – число исходов, благопри-ятных событию В, а т_АВ – число исходов опыта, при которых происходят оба события (то есть исходов, благоприятных произведению АВ). Тогда число исходов, при которых имеет место событие А + В, равно т_А + т_В – т_АВ (так как в сумме (т_А + т_В) т_АВ учтено дважды: как исходы, благоприятные А, и исходы, благоприятные В). Следовательно, вероятность суммы можно определить по формуле (1.1):

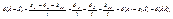
что и требовалось доказать.

Теорему1 можно распространить на случай суммы любого числа событий. Например, для суммы трех событий А, В и С

Р(А + В + С) = р(А) + р(В) + р(С) – р(АВ) – р(АС) – р(ВС) + р(АВС)

Теорема 2. Сумма вероятностей противоположных событий равна 1:

р(А) + р( 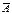) = 1. Доказательство.

Так как А и 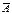образуют полную группу, то одно из них обязательно произойдет в результате опыта, то есть событие А + 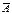является достоверным. Следовательно,

Р( А + 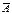) = 1. Но, так как А и 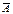несовместны, из (2.4) следует, что Р(А + 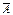) = р(А) + р( 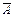). Значит, р(А) + р( 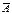) = 1, что и требовалось доказать.

Замечание. В ряде задач проще искать не вероятность заданного события, а вероятность события, противоположного ему, а затем найти требуемую вероятность по формуле (2.5).