Скалярное произведение векторов
Определение 1. Под углом между ненулевыми векторами 
и 
понимаем угол из промежутка [0, p] между представителями этих векторов, отложенных от одной точки.
Угол между векторами и считаем неопределенным, если хотя бы один из векторов нулевой
( иногда его считают равным нулю или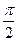 
).
Определение 2. Под скалярным произведением двух ненулевых векторов и понимаем число, равное произведению их длин на косинус угла между ними. Если хотя бы один из векторов нулевой, то под их скалярным произведением понимаем число 0.
Обозначаем : × или ( , ).
Итак,
× = | |×| | cos j.
Следствие 1. 2 = | |2 .
Следствие 2. Пусть и ненулевые векторы. Если их скалярное произведение равно нулю, то они перпендикулярны. Верно и обратное утверждение.
Пусть в базисе {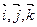 
} заданы векторы ( 
), ( 
), 
( 
).
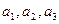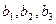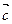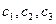Свойство 1. × = 
.
|
|
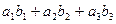Выберем произвольно точку О и от нее откладываем векторы: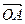 
= , 
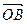= . При этом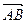 
= − . По теореме косинусов получим ( − )2 = 2 + 2 - 2| |×| | cos j =
= 2 + 2 – 2( , ).
Отсюда находим
( , ) = 
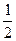( 2 + 2 − ( - )2).
Ранее мы получили формулу | | = 
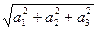для вычисления длины вектора, которую применим к полученному равенству:
( , ) = ( 
+ 
- (( 
)
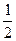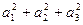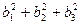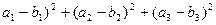и
× = .
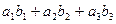Свойство 2. × = × .
Доказательство. Согласно свойству 1 имеем:
× = ,
× = 
.
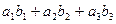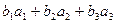Правые части равны, так как произведение действительных чисел обладает свойством коммутативности. Поэтому и левые части рассматриваемых равенств равны, то есть × = × . Свойство доказано.
Свойство 3. l ( , ) = (l , ) = ( , l ).
Докажем, например, равенство: l ( , ) = ( , l ).
Так как
× = ,
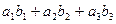то
l 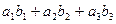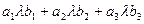( , ) = l( ) = 
= ( , l ).
Свойство 3 доказано.
Свойство 4. ( , + ) = ( , ) + ( , ).
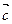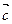Доказательство. ( , + ) = 
=
= ( 
( 
=
= ( 
+ 
=
= ( , 
) + ( , ).
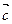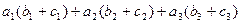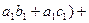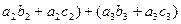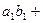
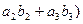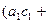
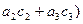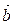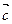Свойство 3 доказано.
Пример 1.В пространстве дан четырехугольник ABCD и известны координаты векторов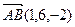 
, 
, 
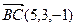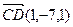. Доказать, что его диагонали взаимно перпендикулярны.
Решение. Для решения задачи достаточно показать перпендикулярность векторов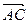 
и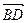 
. Так как = + 
, = + 
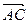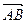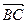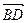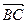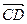, то находим координаты этих векторов: 
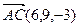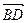, (6, −4, 0). Находим скалярное произведение в координатной форме:
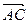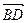× = 6×6 + 9×(−4) +(−3)× 0 = 0.
Следовательно, 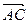^ 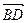и диагонали четырехугольника ABCD взаимно перпендикулярны.
Пример 2.
Выразить квадрат длины медианы треугольника через длины его сторон.
Решение. Рассмотрим в данном треугольнике ABC медиану BB1.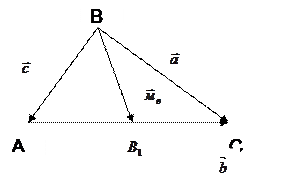 
Введем обозначения: 
= 
, 
= 
, 
= 
,
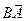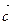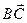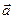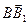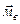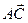= . Тогда справедливо следующее равенство: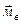 
= ( 
).
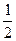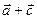Возведем обе части данного равенства в квадрат (скалярно):
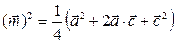(1)
Воспользуемся равенством:
.
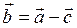После возведения обеих его частей скалярно в квадрат получим:
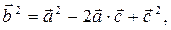
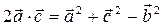. (2)
Тогда из равенств (1) и (2) вытекает следующее равенство:
.
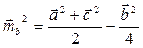Учитывая следствие 1, последнее равенство можно записать следующим образом:
,
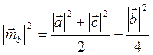т.е.
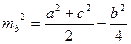, где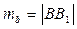 
, 
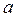=|BC|, b=|AC|, 
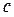=|AB|.
Пример 3.
Дан треугольник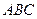 
. Отрезок 
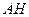- его высота. Выразить вектор 
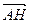через векторы 
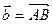и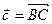 
.
Решение.
|
|
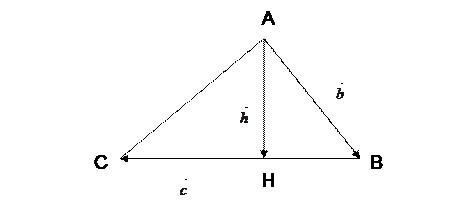
Так как векторы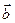 
и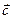 
неколлинеарные, то представляют собой базис двумерного векторного пространства. Введем обозначение: 
.
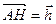По правилу треугольника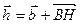 
(1) и, при этом, 
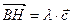(2).
Из равенства (1) и (2) получаем: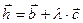 
(3).
Осталось найти число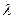 
. Для этого используем ортогональность векторов 
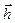и 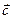, откуда имеем: 
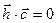(4).
Из равенств (3) и (4) получаем: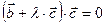 
,
т. е.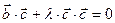 
или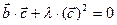 
,
откуда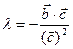 
(5).
Учитывая, что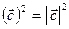 
, равенство (5) можно записать следующим образом: 
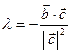(6).
Тогда из равенств (3) и (6) находим вектор :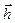
.
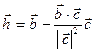Для дальнейшего изложения нам необходимы некоторые сведения из курса алгебры.