В.а.долженков, е.г.соловьева
В.А.ДОЛЖЕНКОВ, Е.Г.СОЛОВЬЕВА
ЭЛЕМЕНТЫ ВЕКТОРНОЙ АЛГЕБРЫ.
МЕТОДИКА РЕШЕНИЯ ЗАДАЧ
|
|


 |

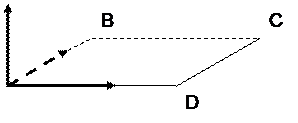 | |||
|
Курск 2006
Составители
Виктор Анатольевич Долженков
Елена Георгиевна Соловьева
Элементы векторной алгебры
и ее методов
Учебно-методтческое пособие
Редактор И.Н.Никитина
Лицензия ИД № 06248 от 12.11.2001 г.
Подписано в печать 10.03.2006. Формат 60х84/16. Печать офсетная.
Усл.печ. л. 3. Тираж 50 экз. Заказ
Курский государственный университет
305000, г. Курск, ул. Радищева, 33
Отпечатано в лаборатории
информационно - методического
обеспечения КГУ
Курский государственный университет
Кафедра геометрии
ОГЛАВЛЕНИЕ
§ 1. Понятие направления. Направленные отрезки…………… … 4
§ 2. Понятие вектора. Сложение векторов …………… 7
§ 3. Умножение вектора на число. Линейная зависимость
векторов ………… … 12 § 4. Координаты вектора. Векторные пространства V1, V2, V3 …17
§ 5. Скалярное произведение векторов ………………23 § 6. Векторное произведение двух векторов ……………... 29 § 7. Смешанное произведение трех векторов ………………34
Решение нулевого варианта контрольной работы ……………… 38
Тест ……………….40
Список литературы ……………… 42
ЭЛЕМЕНТЫ ВЕКТОРНОЙ АЛГЕБРЫ
Сложение векторов
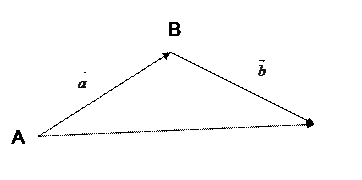
На множестве векторов определяется операция сложение векторов следующим образом. Пусть заданы векторы  и
и  . Выберем произвольно точку А и от точки А откладываем вектор
. Выберем произвольно точку А и от точки А откладываем вектор  . Получим точку В :
. Получим точку В : 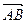 =
=  . Далее, от точки В откладываем вектор
. Далее, от точки В откладываем вектор  . Получим точку С:
. Получим точку С: 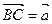 . Точки А и С определяют направленный отрезок
. Точки А и С определяют направленный отрезок 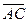 , который в свою очередь определяет вектор
, который в свою очередь определяет вектор 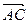 =
= 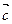 . Вектор
. Вектор 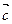 называем суммой векторов
называем суммой векторов  и
и  . Обозначаем:
. Обозначаем:  +
+  =
= 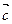 .
.
|

В нашем определении была произвольно выбрана точка А. Поэтому необходимо показать, что от выбора точки А вектор 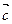 не зависит. Пусть А¢ другая точка. Сделаем те же построения и получим вектор
не зависит. Пусть А¢ другая точка. Сделаем те же построения и получим вектор 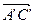 . Покажем, что
. Покажем, что 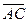 ~
~ 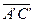 . Действительно, из построения имеем, что
. Действительно, из построения имеем, что  ~
~ 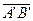 и
и 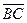 ~
~ 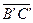 . Согласно теореме 1 имеем:
. Согласно теореме 1 имеем: 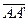 ~
~ 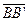 и
и 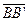 ~
~ 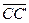 . В силу транзитивности отношения эквиполлентности направленных отрезков получим
. В силу транзитивности отношения эквиполлентности направленных отрезков получим 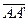 ~
~ 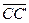 . Отсюда, согласно теореме 1 имеем:
. Отсюда, согласно теореме 1 имеем: 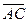 ~
~ 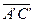 , а это говорит о том
, а это говорит о том 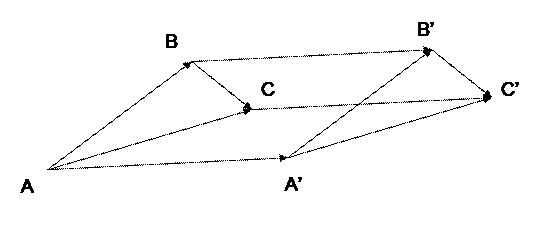 , что от выбора точки А вектор
, что от выбора точки А вектор 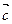 не зависит.
не зависит.
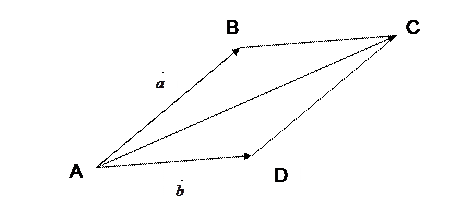
Указанное здесь правило сложения векторов называют правилом треугольника.
Если векторы  и
и  не коллинеарные, то откладывая от точки А оба вектора
не коллинеарные, то откладывая от точки А оба вектора  и
и  , мы получим их сумму как вектор определенный направленным отрезком
, мы получим их сумму как вектор определенный направленным отрезком 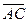 , где точка С - вершина параллелограмма, построенного на представителях векторов
, где точка С - вершина параллелограмма, построенного на представителях векторов  и
и  , отложенных от точки А и противоположная точке А. Действительно, если применить правило треугольника, то получим
, отложенных от точки А и противоположная точке А. Действительно, если применить правило треугольника, то получим
 +
+  =
= 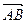 +
+ 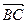 =
= 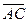 .
.

Пример 2.
Пользуясь параллелограммом, построенном на представителях векторов 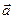 и
и 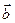 , проверить на чертеже справедливость тождества:
, проверить на чертеже справедливость тождества: 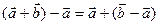 .
.
Решение.
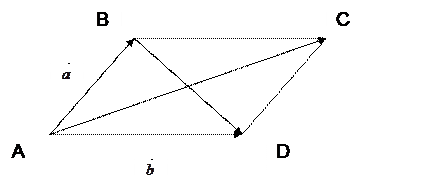

По условию 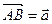 ,
, 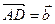 . Обозначим левую часть тождества
. Обозначим левую часть тождества 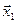 , правую
, правую 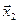 . Покажем, что
. Покажем, что 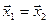 . По правилу параллелограмма
. По правилу параллелограмма 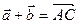 , тогда
, тогда 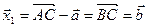 . Таким образом,
. Таким образом, 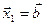 . (1)
. (1)
Так как 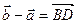 , то
, то 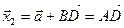 , откуда
, откуда 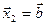 . (2)
. (2)
Из равенств (1) и (2) следует, что 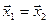 . Тем самым тождество доказано.
. Тем самым тождество доказано.
Умножение вектора на число. Линейная
Зависимость векторов
Определение 1. Под произведением действительного числа l на вектор  понимаем новый вектор
понимаем новый вектор  , который удовлетворяет следующим требованиям:
, который удовлетворяет следующим требованиям:
1). Если l = 0 или  =
= 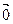 , то
, то  =
= 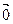 .
.
2). Если l ¹ 0 и  ¹
¹ 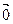 , то вектор
, то вектор  задаем следующими условиями:
задаем следующими условиями:
а) |  | = |l| |
| = |l| |  |,
|,
б) 
 , если l > 0 и
, если l > 0 и  ¯
¯  , если l < 0.
, если l < 0.
Обозначаем:  = l
= l  .
.
Пример1.
Дан ортонормированный базис 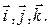 В этом базисе задан вектор
В этом базисе задан вектор 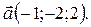 Найти координаты вектора
Найти координаты вектора 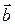 , который коллинеарен вектору
, который коллинеарен вектору 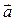 и имеет длину, равную 5.
и имеет длину, равную 5.
Решение. Из коллинеарности векторов 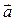 и
и 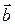 следует, что существует единственное число a ¹ 0, такое что
следует, что существует единственное число a ¹ 0, такое что 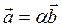 . Так как
. Так как 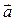 (–1; -2; 2), то координаты вектора
(–1; -2; 2), то координаты вектора 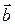 будут соответственно равны
будут соответственно равны  (
( 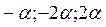 )
)
Из условия, что длина вектора 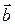 равна 5, получаем следующее равенство:
равна 5, получаем следующее равенство: 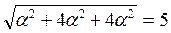 , откуда
, откуда
9 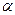 2 =25,
2 =25, 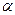 2 =
2 = 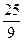 ,
, 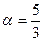 или
или 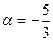 .
.
Последнее означает, что задача имеет два решения:
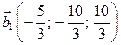 ,
, 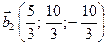 .
.
Пример 2.
Треугольник АВС построен на векторах 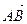 (0,-3,4) и
(0,-3,4) и
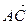 (2,-1,2) в ортонормированном базисе
(2,-1,2) в ортонормированном базисе 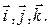 .
.
Найти координаты вектора, параллельного биссектрисе угла ВАС.
Решение.
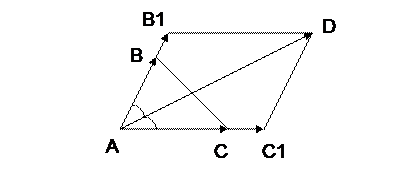

Построим вектора 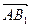 и
и 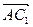 такие, что:
такие, что: 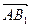
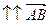 и
и 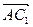
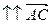 , причем
, причем 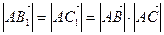 . На данных векторах построим ромб
. На данных векторах построим ромб 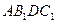 . Диагональ AD ромба
. Диагональ AD ромба 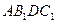 лежит на биссектрисе угла
лежит на биссектрисе угла 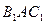 . Следовательно, вектор
. Следовательно, вектор 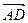 параллелен биссектрисе угла
параллелен биссектрисе угла 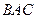 и, при этом,
и, при этом, 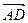 =
= 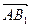 +
+ 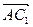 (1).
(1).
Из построения векторов 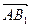 и
и 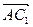 получаем следующие равенства:
получаем следующие равенства:
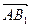 =
= 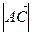
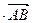 и
и 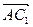 =
= 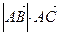 .
.
Из последних равенств и равенства (1) следует, что
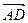 =
= 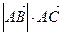 +
+ 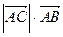 .
.
Так как 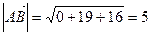 и
и 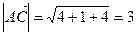 , то
, то
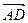 =5
=5 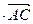 +3
+3 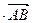 ,
,
откуда
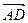 (10;−14;22).
(10;−14;22).
Так как вектор 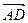 параллелен биссектрисе угла
параллелен биссектрисе угла 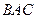 , то и вектор
, то и вектор 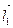 (5,−7,11) будет параллельным этой биссектрисе. Любой другой вектор
(5,−7,11) будет параллельным этой биссектрисе. Любой другой вектор 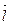 , параллельный биссектрисе угла
, параллельный биссектрисе угла 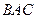 , будет иметь координаты
, будет иметь координаты
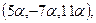 где
где 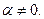
Таким образом, решением является вектор 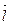
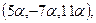 где
где 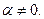
Пример 3.
Дан параллелепипед 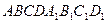 . Точки
. Точки 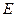 и
и 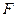 - середины соответственно ребер
- середины соответственно ребер 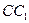 и
и 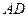 . В качестве базисных векторов взяты векторы
. В качестве базисных векторов взяты векторы 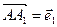 ,
, 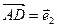 ,
, 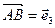 . Найти координаты векторов
. Найти координаты векторов 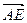 ,
, 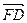 и
и 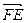 в данном базисе.
в данном базисе.
Решение.
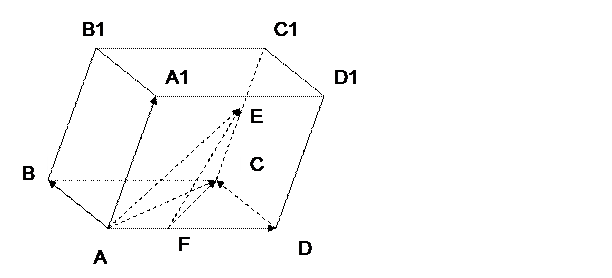

1) 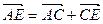 (1),
(1), 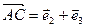 (2),
(2),
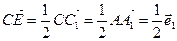 , откуда
, откуда 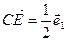 (3).
(3).
Из равенств (1), (2), (3) следует, что 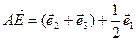 .
.
Используя свойства коммутативности и ассоциативности операции сложения векторов, получаем следующее равенство: 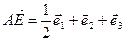 .
.
Следовательно, 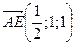 .
.
2) 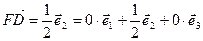 , откуда получаем:
, откуда получаем: 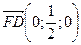 .
.
3) 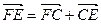 (1),
(1), 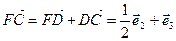 , откуда
, откуда 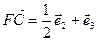 (2),
(2),
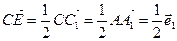 , откуда
, откуда 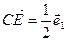 (3).
(3).
Из равенств (1), (2) и (3) имеем: 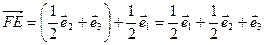 .
.
Следовательно, 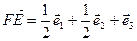 , откуда
, откуда 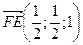 .
.
Пример 2.
Выразить квадрат длины медианы треугольника через длины его сторон.
Решение. Рассмотрим в данном треугольнике ABC медиану BB1. 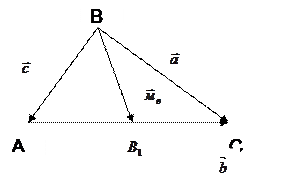 Введем обозначения:
Введем обозначения: 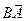 =
= 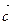 ,
, 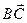 =
= 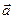 ,
, 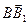 =
= 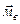 ,
,
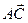 =
=  . Тогда справедливо следующее равенство:
. Тогда справедливо следующее равенство: 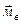 =
= 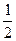 (
( 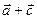 ).
).
Возведем обе части данного равенства в квадрат (скалярно):
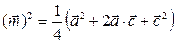 (1)
(1)
Воспользуемся равенством:
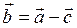 .
.
После возведения обеих его частей скалярно в квадрат получим:
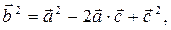
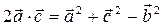 . (2)
. (2)
Тогда из равенств (1) и (2) вытекает следующее равенство:
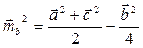 .
.
Учитывая следствие 1, последнее равенство можно записать следующим образом:
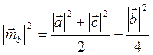 ,
,
т.е.
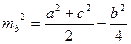 , где
, где 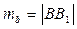 ,
, 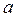 =|BC|, b=|AC|,
=|BC|, b=|AC|, 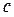 =|AB|.
=|AB|.
Пример 3.
Дан треугольник 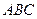 . Отрезок
. Отрезок 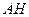 - его высота. Выразить вектор
- его высота. Выразить вектор 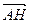 через векторы
через векторы 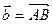 и
и 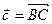 .
.
Решение.
|
|
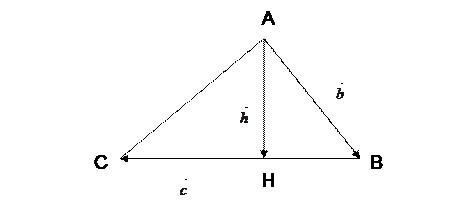

Так как векторы 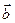 и
и 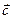 неколлинеарные, то представляют собой базис двумерного векторного пространства. Введем обозначение:
неколлинеарные, то представляют собой базис двумерного векторного пространства. Введем обозначение: 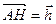 .
.
По правилу треугольника 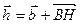 (1) и, при этом,
(1) и, при этом, 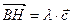 (2).
(2).
Из равенства (1) и (2) получаем: 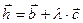 (3).
(3).
Осталось найти число 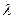 . Для этого используем ортогональность векторов
. Для этого используем ортогональность векторов 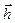 и
и 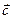 , откуда имеем:
, откуда имеем: 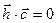 (4).
(4).
Из равенств (3) и (4) получаем: 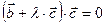 ,
,
т. е. 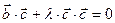 или
или 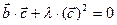 ,
,
откуда 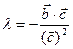 (5).
(5).
Учитывая, что 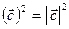 , равенство (5) можно записать следующим образом:
, равенство (5) можно записать следующим образом: 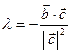 (6).
(6).
Тогда из равенств (3) и (6) находим вектор 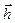 :
:
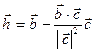 .
.
Для дальнейшего изложения нам необходимы некоторые сведения из курса алгебры.
Пример 1.
Дан параллелепипед ABCDA1B1C1D1 и координаты следующих векторов в ортонормированном базисе: 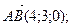
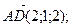
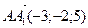 .
.
Найти: 1) объем параллелепипеда;
2) площади граней ABCD и CDD1C;
3) косинус двугранного угла между плоскостями ABC и CDD1.
Решение.
1) Данный параллелепипед построен на векторах 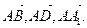
Таким образом, его объем равен модулю смешанного произведения этих векторов, т.е.
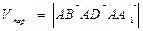
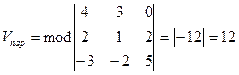 (куб.ед.)
(куб.ед.)
Итак, Vпар=12 куб.ед.
2) Напомним, что площадь параллелограмма равна длине векторного произведения векторов, на которых он построен.
Т.о. 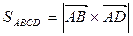 .
.
Введем обозначение: 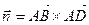 ,тогда
,тогда 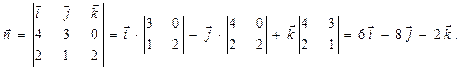
Следовательно, 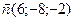 , откуда
, откуда
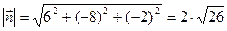 .
.
Т.о. 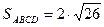 кв.ед.
кв.ед.
Аналогично, 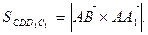
Пусть 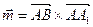 , тогда
, тогда
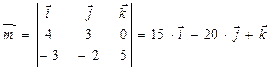 ,
,
откуда 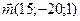 и
и 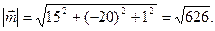
Значит 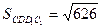 кв.ед.
кв.ед.
3) Введем следующие обозначения: пл. (АВС)= 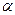 , пл. (DCC1)=
, пл. (DCC1)= 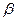 .
.
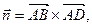
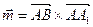 .
.
Согласно определению векторного произведения имеем:
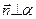 и
и 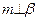 .
.
А значит справедливо следующее равенство: 

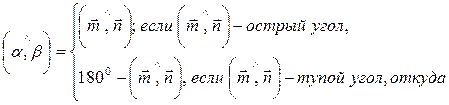
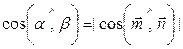 .
.
Из второго пункта решения имеем:
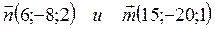 .
.
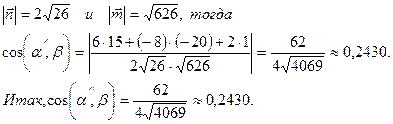
Пример 2.
Доказать, что если 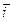 ,
, 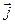 ,
, 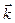 - взаимно перпендикулярные единичные векторы, то для любых векторов
- взаимно перпендикулярные единичные векторы, то для любых векторов 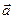 и
и 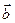 справедливо равенство:
справедливо равенство: 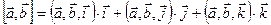 (1).
(1).
Решение.
Пусть в ортонормированном базисе { 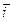 ,
, 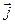 ,
, 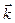 } заданы координаты векторов:
} заданы координаты векторов: 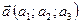 ;
; 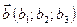 . Так как
. Так как 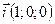 ,
, 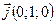 ,
, 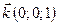 , то по свойству смешанного произведения имеем:
, то по свойству смешанного произведения имеем:
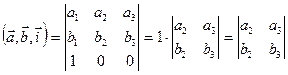 .
.
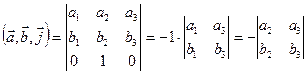 .
.
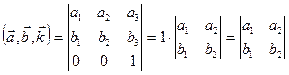 .
.
Таким образом, равенство (1) можно записать в следующей форме: 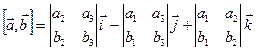 , а это одно из доказанных свойств векторного произведения векторов
, а это одно из доказанных свойств векторного произведения векторов 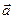 и
и 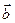 . Тем самым справедливость равенства (1) доказана.
. Тем самым справедливость равенства (1) доказана.
Решение нулевого варианта
Контрольной работы
Задание № 1.
Вектор 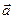 образует с базисными векторами
образует с базисными векторами 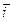 и
и 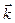 соответственно углы
соответственно углы 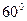 и
и 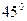 . Определить угол, который образует вектор
. Определить угол, который образует вектор 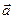 с вектором
с вектором 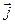 .
.
Решение.
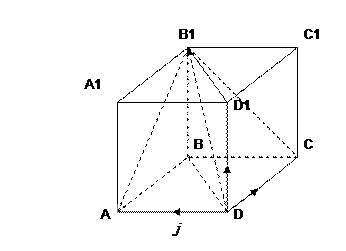

Построим параллелепипед 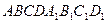 на векторах
на векторах 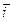 ,
, 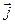 ,
, 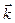 и диагональю
и диагональю 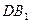 , такой, что векторы
, такой, что векторы 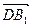 и
и 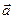 равны.
равны.
Тогда в прямоугольном треугольнике 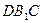 с прямым углом
с прямым углом 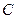 , величина угла
, величина угла 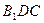 равна
равна 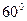 , откуда
, откуда 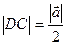 .
.
Аналогично в прямоугольном треугольнике 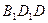 с прямым углом
с прямым углом 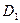 величина
величина 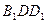 равна
равна 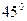 , откуда
, откуда 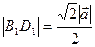 .
.
В прямоугольном треугольнике 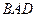 по теореме Пифагора
по теореме Пифагора 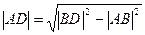 , но
, но 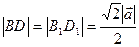 и
и 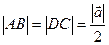 , тогда
, тогда 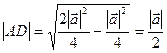 .
.
В прямоугольном треугольнике 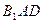 с прямым углом
с прямым углом  катет
катет 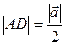 , а гипотенуза
, а гипотенуза 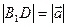 . Значит, величина угла
. Значит, величина угла 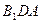 равна
равна  . Но угол
. Но угол 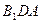 равен углу между векторами
равен углу между векторами 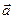 и
и 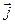 . Тем самым задача решена.
. Тем самым задача решена.
Задание № 2.
Заданы три вектора 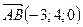 ,
, 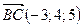 ,
, 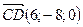 в базисе {
в базисе { 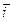 ,
, 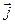 ,
, 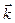 }. Доказать, что четырехугольник
}. Доказать, что четырехугольник 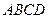 - плоский, найти его площадь.
- плоский, найти его площадь.
Решение.
1) Если векторы 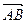 ,
, 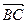 и
и 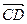 компланарные, то
компланарные, то 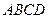 - плоский четырехугольник. Вычислим определитель, составленный из координат данных векторов.
- плоский четырехугольник. Вычислим определитель, составленный из координат данных векторов.
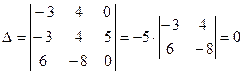 .
.
Так как определитель равен нулю, то векторы 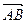 ,
, 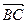 и
и 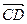 компланарные, а значит, четырехугольник
компланарные, а значит, четырехугольник 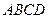 - плоский.
- плоский.
2) Заметим, что 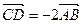 , поэтому
, поэтому 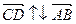 и
и 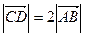 , таким образом четырехугольник
, таким образом четырехугольник 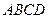 трапеция с основаниями АВ и CD.
трапеция с основаниями АВ и CD.
|
|

Тогда 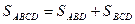 . А по свойству векторного произведения
. А по свойству векторного произведения 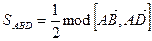 ,
, 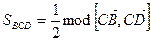 .
.
Так как 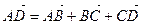 , то
, то 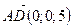
Так как 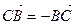 , то
, то 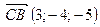
По одному из свойств векторного произведения имеем:
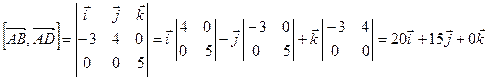 , откуда
, откуда 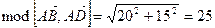 .
.
Значит 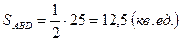 .
.
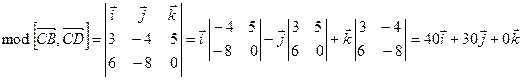 , откуда
, откуда 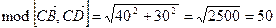 .
.
Значит 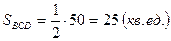 .
.
Тогда 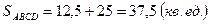
Задание № 3.Найти вектор 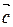 , коллинеарный вектору
, коллинеарный вектору 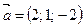 , у которого длина равна 5.
, у которого длина равна 5.
Решение.
Обозначим координаты вектора 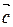 (х, у, z). Как известно, у коллинеарных векторов координаты пропорциональны, и поэтому имеем:
(х, у, z). Как известно, у коллинеарных векторов координаты пропорциональны, и поэтому имеем:
х = 2t, y = t, z = − 2t.
По условию задачи | 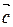 | = 5, а в координатной форме:
| = 5, а в координатной форме: 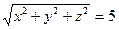 . Выражая переменные через параметр t, получим: 4t2 +t2 +4t2 =25 и t2 =
. Выражая переменные через параметр t, получим: 4t2 +t2 +4t2 =25 и t2 = 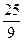 . Таким образом, t = ±
. Таким образом, t = ± 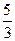 и х = ±
и х = ± 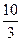 , у = ±
, у = ± 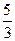 , z =
, z = 
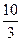 . Получили два решения:
. Получили два решения: 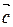 1 (
1 ( 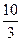 ;
; 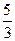 ; −
; − 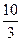 ),
), 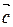 2 (−
2 (− 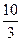 ;−
;− 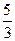 ;
; 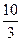 ).
).
Тест
Вариант 0.
А 1. Лучи [А, В) и [С, D), лежащие на одной прямой (А, В) называются сонаправленными, если
Вар. отв.: 1) они лежат в одной полуплоскости с границей (А,С);
2) их пересечением является луч; 3) они не пересекаются;
4) другой ответ.
А 2. Свойство лучей быть противоположно направленными
Вар. отв.: 1) транзитивно; 2) симметрично; 3) рефлексивно; 4) другой ответ
А 3. Вектором в пространстве мы называем
Вар. отв.: 1) отрезок; 2) направленный отрезок; 3) класс эквиполлентных направленных отрезков; 4; другой ответ.
А 4. Вычислить определитель: 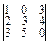 .
.
Вар. отв.: 1) 17; 2) 16; 3) –17; 4) 12.
А 5. Найти длину вектора 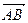 (5, 4, 0).
(5, 4, 0).
Вар. отв.: 1) 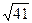 ; 2)
; 2) 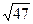 ; 3) 9; 4) др.отв.
; 3) 9; 4) др.отв.
А 6. При каком значении 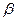 векторы
векторы 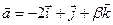 и
и 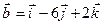 взаимно перпендикулярны?
взаимно перпендикулярны?
Вар. отв.: 1) 5; 2) -4; 3) 10; 4) 4.
А 7. Найти сумму 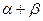 , если векторы
, если векторы 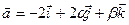 и
и 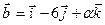 коллинеарные.
коллинеарные.
Вар. отв.: 1)6 ; 2) 18 ; 3) -6 ; 4) 0 .
А 8. Если 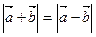 , то векторы
, то векторы 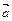 и
и 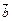
1) сонаправлены; 2) противоположно направлены; 3) перпендикулярны, 4) равны.
А 9. Дано: 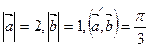 . Модуль вектора
. Модуль вектора 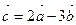 равен
равен
1) 1; 2) 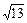 ; 3)
; 3) 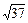 , 4) 5.
, 4) 5.
А 10. Вычислить определитель: 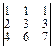 .
.
1) 1; 2) 3; 3) -1, 4) -3.
А 11. Найти векторное произведение векторов  (0; -1; 1).
(0; -1; 1).  (1; -1; 3)
(1; -1; 3)
Вар. отв.: 1) 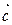 (-2; -1; 1); 2)
(-2; -1; 1); 2) 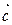 (-2; 1; 1); 3)
(-2; 1; 1); 3) 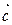 (2; 1; 2); 4) др.отв.
(2; 1; 2); 4) др.отв.
А 12. Найти площадь треугольника, построенного на векторах 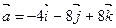 и
и 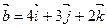 .
.
1) 30; 2) 15; 3) 60, 4) др.
А 13. Какая из следующих троек векторов 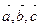 является компланарной?
является компланарной?
1) 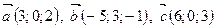 . 2)
. 2) 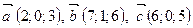 ;
;
3) 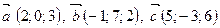 ; 4)
; 4) 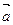 (1; –2; 1),
(1; –2; 1), 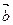 (3; 2; 1) ,
(3; 2; 1) , 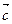 (1; 0; –1).
(1; 0; –1).
А 14. Найти вектор 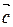 , перпендикулярный векторам
, перпендикулярный векторам 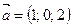 и
и 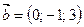 такой, что
такой, что 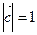 , и при этом тройка векторов
, и при этом тройка векторов 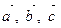 - левая.
- левая.
1) 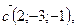 2)
2) 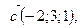 3)
3) 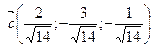 , 4)
, 4) 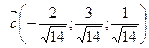 .
.
А 15. Найти объем параллелепипеда, построенного на векторах
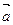 (1; –2; 1),
(1; –2; 1), 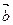 (3; 2; 1) и
(3; 2; 1) и 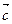 (1; 0; –1).
(1; 0; –1).
1) 24; 2) 10; 3) 12.; 4) 0.
| № | |||||||||||||||
| отв |
Список литературы
1. А.Д. Александров, Н.Ю. Нецветаев. Геометрия. - М.: Наука, 1990.
2. Л.С. Атанасян, В.Т. Базылев. Геометрия. Ч. 1. - М.: Просвещение, 1986.
3. В.Т. Базылев, К.И. Дуничев и др. Геометрия. - Ч. 1. - М.: Просвещение, 1974.
4. В.Т. Базылев, К.И. Дуничев и др. Под ред. В.Т. Базылева. Сборник задач по геометрии. - М.: Просвещение, 1980.
5. Беклемишева Л.А. и др. Сборник задач по аналитической геометрии: Уч.пособие. –М.:, 2003.
6. Бортаковский А.С., Пантелеев А.В. Аналитическая геометрия в примерах и задачах: Учебное пособие. –М.: Высшая школа, 2005.
7. А.Л. Вернер, Б.Е. Кантор, С.А. Франгулов. Геометрия, ч.1.- С. Петербург, 1997.
8. Л.С. Атанасян, В.А. Атанасян. Сборник задач по геометрии. Ч. 1. - М.: Просвещение, 1973.
9. Ефимов Н.В., Розендорн Э.Р. Линейная алгебра и многомерная геометрия. –М., 2004. –464 с.
10. Ефимов Н.В. Высшая геометрия: Учебник для вузов. –.М.: Физматлит, 2003. –584 с.
11. Жаферов А.Ф. Геометрия: в 2-х частях. Ч.1. –Новосибирск: Сиб.унив.изд-во, 2002. –271 с.
12. Жаферов А.Ф. Геометрия: в 2-х частях. Ч.2. –Новосибирск: Сиб.унив.изд-во, 2003. –267 с.
13. Кострикин А.И., Манин Ю.И. Линейная алгебра и геометрия. –М.: МГУ, 1980. –320 с.
14. Д.В. Клетеник. Сборник задач по аналитической геометрии. - М.: Наука, 1964.
15. А.В. Погорелов. Геометрия. - М.: Наука, 1984.
16. О.Н. Цубербиллер. Сборник задач по аналитической геометрии. - М.: Наука, 1966.
В.А.ДОЛЖЕНКОВ, Е.Г.СОЛОВЬЕВА
ЭЛЕМЕНТЫ ВЕКТОРНОЙ АЛГЕБРЫ.
МЕТОДИКА РЕШЕНИЯ ЗАДАЧ
|
|


 |

 | |||
|
Курск 2006
Составители
Виктор Анатольевич Долженков
Елена Георгиевна Соловьева
Элементы векторной алгебры
и ее методов
Учебно-методтческое пособие
Редактор И.Н.Никитина
Лицензия ИД № 06248 от 12.11.2001 г.
Подписано в печать 10.03.2006. Формат 60х84/16. Печать офсетная.
Усл.печ. л. 3. Тираж 50 экз. Заказ
Курский государственный университет
305000, г. Курск, ул. Радищева, 33
Отпечатано в лаборатории
информационно - методического
обеспечения КГУ
Курский государственный университет
Кафедра геометрии
ОГЛАВЛЕНИЕ
§ 1
