Соединение фаз приемника треугольником

Активное сопротивление.

Рассмотрим пассивный двухполюсник (рис. 3.6а), для которого входные синусоидаль­ные напряжение и ток согласо­ваны: 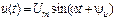; 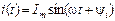. Предста­вим эти синусоиды в виде их комплексных амплитуд (ком­плексных значений):

; .

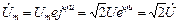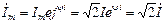Комплексным сопротивлением двухполюсника называют отно­шение

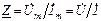, (3.17)

где модуль Z=U_m/I_m=U/I назы­вают также полным сопротивле­нием двухполюсника, а аргумент обозначен через φ, так как он равен сдвигу фаз φ=ψ_u-ψ_i.

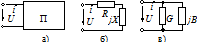
Рис.3.6.

В алгебраической форме сопротивление Z принимает вид:

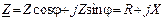, (3.18)

где R=Zcosφ – активная состав­ляющая Z; X=Zsinφ – реактивная составляющая Z. Комплексной проводимостью Y двухполюсника называют отношение

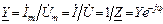, (3.19)

где модуль Y=I/U=1/Z называют полной проводимостью, а аргу­мент Y равен сдвигу фаз со зна­ком минус, т.е. –φ. В алгебраиче­ской форме проводимость Y имеет вид

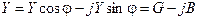, (3.20)

где G = Ycosφ – активная состав­ляющая Y; B = Ysinφ –реактивная составляющая Y.

Определим комплексные сопротивления и проводимости простейших двухполюсников.

Резистивный элемент (сопротивление R). Пусть к R-элементу приложено напряжение u_R(t)=U_msin(ωt) (рис.3.7а). Тогда i(t)=u_R(t)/R=U_msin(ωt)/R=I_msin(ωt), где I_m=U_m/R. Для комплексных амплитуд напряжения и тока по­лучим: ; .

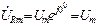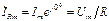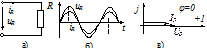
Рис. 3.7. Схема, временные и век

­торные диаграммы резистивного элемента

Комплексное сопротивление R-элемента

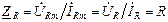. (3.21)

Таким образом, комплексное со­противление R-элемента содер­жит только активную составляю­щую R. Сопротивление R-эле­мента в цепях переменного тока называют активным сопротивле­нием. Сдвиг фаз φ=ψ_u – ψ_i=0, т.е. ток и напряжение R-элемента совпадают по фазе. Этот факт от­ражают временные диаграммы на рис. 3.7б и векторная диаграмма на рис. 3.7в, на которой в целях различения вектор тока условно смещен вверх. Комплексная про­водимость R-элемента также со­держит только активную состав­ляющую:

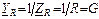. (3.22)

8. Последова­тельное соединение ак­тивного сопротивления и катушки индуктивно­сти. Схема, уравнения напряжений, треуголь­ник напряжений. Век­торная диаграмма.

9. Последова­тельное соединение ак­тивного и емкостного сопротивлений. Схема. Треугольник напряже­ний. Диаграмма.

10. Последова­тельное соединение ак­тивного, емкостного и активно-индуктивного сопротивлений. Второй закон Кирхгофа для напряжений. Схема. Векторная диаграмма.

Рассмотрим неразветв­ленную цепь на рис. 3.10а, кото­рая содержит приборы электро­магнитной системы, измеряющие действующие значения величин.

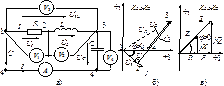Рис. 3.10. Цепь с последовательным соединением элементов (а)), вектор­ная диаграмма напряжений (б)), сопротивлений и мощностей (в)) при X_L>X_C

Цепь содержит последо­вательное соединение элементов, поэтому на основе аналогии с це­пями постоянного тока входное сопротивление цепи находим как сумму комплексных сопротивле­ний:

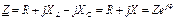, (3.40)

где X=X_L-X_C – реактивное сопро­тивление цепи; Z=(X²+R²)^0,5 – полное сопротивление; φ=arctg(X/R) – сдвиг фаз входного напряжения и тока. Пусть вход­ное напряжение имеет нулевую начальную фазу, т.е. 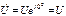. Тогда

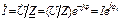. (3.41)

Показание амперметра, изме­ряющего действующее значение тока I

.

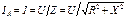Комплексные напряжения эле­ментов цепи находим по закону Ома:

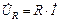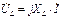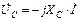; ; . (3.42)

Действующие значения этих на­пряжений измеряют V₁, V₂, V₄:

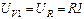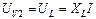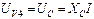; ; . (3.43)

Элементы R и L могут быть со­ставляющими последовательной схемы замещения реальной ка­тушки индуктивности. Катушка имеет выводы 1 и 3, напряжение 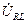между которыми найдем по закону Ома:

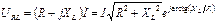. (3.44)

Разумеется, 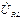можно найти и так: .

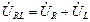Определим мощности каждого из элементов цепи. Рези­стивный элемент развивает ак­тивную мощность:

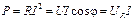, (3.45)

а реактивные мощности L- и C- элементов Q_L=X_LI², Q_C=-X_CI²; в сумме образуют реактивную мощность цепи:

.

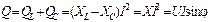11. Резонанс на­пряжений. Условия по­лучения резонанса на­пряжений. Общее со­противление, коэффи­циент мощности, вели­чина тока и мощности при резонансе напря­жений.

Режим, при котором в цепи, содержащей L- и C- эле­менты, входные напряжение и ток совпадают по фазе, называют ре­зонансом. Итак, X_L=X_C – условие резонанса напряжений. Если это условие разрешить относительно частоты ω, то получим:

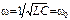. (3.48)

Частоту ω₀ называют резонансной частотой. Явление резонанса бла­годаря ряду особенностей широко используется в радиоэлектронике, электротехнике, электросвязи и т.д. Резонанса можно достичь из­менением частоты источника или параметров L, С контура. Далее будем считать, что изменяется только ω, а параметры контура постоянны.

При резонансе сопро­тивление контура минимально и равно R

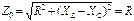. (3.49)

Ток, как функция частоты, при резонансе максимален

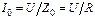. (3.50)

Величину

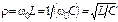(3.51)

называют характеристическим сопротивлением контура, а отно­шение

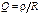(3.52)

называют добротностью контура.

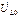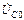На рис. 3.11а представ­лена векторная диаграмма кон­тура при резонансе. Из равенства X_L=X_C следует равенство напря­жений U_L0=U_C0=ρI₀=UQ, т.е. при резонансе показания вольтметров V₂ и V₄ одинаковы и превышают входное напряжение U в Q раз. Добротность контуров, исполь­зуемых в радиоэлектронике, дос­тигает нескольких сотен. Напря­жения и находятся в про­тивофазе (сдвинуты по фазе на 180°), поэтому их сумма равна нулю (вольтметр, подключенный к точкам 2 и 4, покажет нуль). Из ВЗК следует, что при резонансе все выходное напряжение 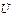при­ложено к R-элементу: .

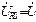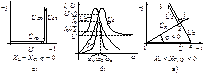
Рис. 3.11. Диаграммы последова­тельного контура

Частотной характери­стикой какой-либо величины на­зывают ее зависимость от час­тоты. На рис. 3.11б представлены частотные характеристики тока I(ω) и напряжений U_L(ω) и U_C(ω). Полосой пропускания П контура называют диапазон частот, для которого I(ω)≥ 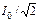. Из рис. 3.11б видно, что П 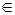[ω_н, ω_в]. Ширина полосы пропускания ΔП=ω_в–ω_н и добротность Q свя­заны как:

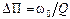. (3.53)

При снижении сопротивления R контура с сохранением L и C рас­тут величины Q, I₀, U_L0=U_C0 и уменьшается ΔП. С ростом доб­ротности контура резонансные кривые на рис. 3.11б становятся уже и вытягиваются вверх. Гово­рят, что при этом растет избира­тельность контура, т.е. способ­ность контура резко усиливать напряжения U_L и U_C в узкой час­тотной области П, примыкающей к частоте ω₀. Резонанс в последо­вательном контуре называют ре­зонансом напряжений.

В тех случаях, когда ре­жим резонанса в цепи не преду­смотрен, случайная настройка контура в резонанс может при­вести к повреждению элементов контура (перегоранию резистора или катушки, пробою изоляции катушки или диэлектрика кон­денсатора). При резонансе актив­ная мощность цепи максимальна P=RI₀²=max, а реактивная мощ­ность Q=(X_L0–X_C0)I₀²=0. Равенство Q=0 говорит об отсутствии об­мена между контуром и источни­ком. Обмен энергией наблюда­ется между магнитным полем L-элемента и электрическим полем емкости C.

Третий случай при X_L<X_C. При таком соотношении параметров X=X_L–X_C<0, т.е. φ=arctg(X/R)<0, т.е. ток I опережает по фазе на­пряжение U (рис. 3.11в). Из нера­венства X_C>X_L следует неравен­ство X_CI>X_LI, т.е. U_C>U_L. Топо­графическая диаграмма на рис. 3.11в подтверждает это нера­венство. Из X<0 следует также Q=XI²=(X_L–X_C)I²<0. Треугольники сопротивлений и мощностей для случая X,Q<0 можно получить «опрокидыванием» относительно оси +1 треугольников на рис. 3.10в

12. Параллельное соединение сопротив­лений в цепи перемен­ного тока. Схема. Об­щий ток и сдвиг фаз между током и напря­жением каждой ветви цепи. Треугольник то­ков. Активная, реак­тивная и полная мощ­ности. Векторная диа­грамма.

На рис. 3.12 представ­лена параллельная цепь из эле­ментов R, L, C и приборов элек­тромагнитной системы, изме­ряющих действующие значения величин. Анализ цепи произведем комплексным методом. Пусть за­дано напряжение 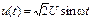, т.е. .

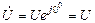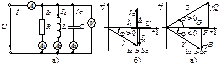
Рис. 3.12. Цепь с параллельным соединением элементов (а)), век­торная диаграмма токов (б)), про­водимостей и мощностей (в)) при b_L>b_C

Определим комплексные проводимости ветвей:

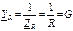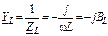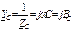; ; .(3.54)

Тогда комплексная проводимость цепи

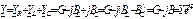, (3.55)

где 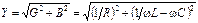– полная проводимость цепи; 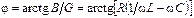– сдвиг фаз между входными на­пряжением и током; B=B_L–B_C – реактивная проводимость цепи.

По закону Ома находим комплексный входной ток:

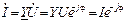, (3.56)

где I=YU – измеряемое ампермет­ром А действующее значение входного тока. В схеме замеще­ния на рис. 3.12а все проводники идеальные, поэтому входное на­пряжение 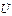без потерь переда­ется к каждой из параллельных ветвей цепи. Вольтметр V изме­ряет действующее значение U входного напряжения. При необ­ходимости ток каждой ветви можно рассчитать по закону Ома:

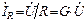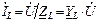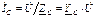; ; . (3.57)

Векторную диаграмму токов строят на основе ПЗК:

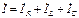. (3.58)

Знак угла φ может быть разным в зависимости от соотношения ме­жду проводимостями B_L и B_C:

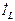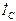Первый случай B_L>B_C. При этом B=B_L–B_C>0 и, согласно (3.55), угол φ положителен (φ > 0). Из соотношения B_L>B_C следует неравенство B_LU>B_CU, т.е. I_L>I_C. Векторная диаграмма токов и напряжения изображена на рис. 3.12б. Токи и обра­зуют реактивную составляющую 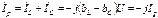, где I_р=|b_L–b_C|U. Реактивная со­ставляющая 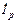отстает по фазе от напряжения 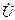на 90°, т.е. но­сит индуктивный характер. Ак­тивная составляющая 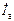, совпа­дающая по фазе с 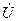, равна току 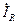. 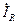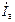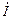Токи , и образуют треугольник токов.

Рассчитаем комплекс­ную мощность цепи:

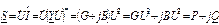,(3.60)

где Q=BU²=(B_L–B_C)U²=X_LI_L²–X_CI_C² – реактивная мощность цепи; P=GU²=U²/R=RI_R² – активная мощность цепи. Поскольку B>0, то Q>0. Подобные треугольники проводимостей и мощностей по­строены на рис. 3.12в, причем уч­тено, что аргументом комплекс­ной проводимости 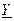является угол «–φ».

Второй случай B_L<B_C. Теперь B=B_L–B_C<0 и угол φ, со­гласно (3.55), становится отрица­тельным (φ<0). Для реактивных токов получаем неравенство I_L<I_C. На рис. 3.13а приведена диаграмма токов и напряжения цепи. Поскольку I_C>I_L, т.е. емко­стная составляющая тока преоб­ладает, то реактивная составляю­щая также имеет емкостный характер. Для мощностей спра­ведливы формулы (3.60) с той лишь разницей, что теперь B, φ, Q<0, что и отражают треуголь­ники проводимостей и мощно­стей на рис. 3.13б.

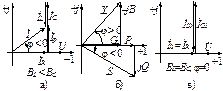Рис. 3.13.

Третий случай B_L=B_C. Отсюда по­лучаем φ=0, что свидетельствует о наличии резонанса в цепи.

15. Резонанс то­ков. Условия получе­ния резонанса токов. Общая проводимость, коэффициент мощно­сти, величина тока и мощности при резо­нансе. Область приме­нения резонансов.

Из равенства проводи­мостей следует равенство B_LU=B_CU, т.е. I_L0=I_C0. Векторная диаграмма токов и напряжения цепи при резонансе показана на рис. 3.13в. Из диаграммы видно, что ток совпадает по фазе с напряжением , как и должно быть при резонансе. Резонанс в параллельной цепи называют ре­зонансом токов. Раскроем усло­вие резонанса B_L=B_C:

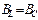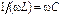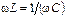; ; . (3.61)

Таким образом, условие резо­нанса токов для цепи на рис. 3.12а совпадает с условием X_L=X_C резонанса напряжений в последовательном контуре. Резо­нансная частота ω₀ параллельной цепи определяется формулой (3.48).

Рассмотрим подробнее свойства реактивной части цепи на рис. 3.12а, т.е. контура, со­стоящего из параллельно вклю­ченных L- и C-элементов. Из век­торной диаграммы видно, что входной ток I_р=I_L0+I_C0 этого иде­ального LC-контура при резо­нансе равен нулю, что указывает на бесконечно большое резонанс­ное сопротивление Z_к контура. Это можно доказать прямым вы­числением:

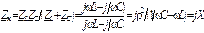. (3.62)

При резонансе в знаменателе Z_к имеется нуль, т.е. Z_к=∞. Частот­ная характеристика полного со­противления идеального LC-кон­тура. Z_к(ω)=|X(ω)|, построенная по выражению (3.62), изображена на рис.3.14а. На рис. 3.14б пока­заны частотные характеристики токов I_L(ω), I_C(ω), I_p(ω), построен­ные по выражениям I_L(ω)=U/(ωL); I_C(ω)=ωCU; I_p(ω)=|I_L(ω)-I_C(ω)|; а на рис. 3.14в – частотная характе­ристика входного тока I(ω), по­строенная по выражению 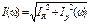, где I_R=U/R=const.

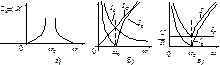
Рис. 3.14. Частотные характери­стики параллельного колебатель­ного контура

В электронике приме­няют параллельные контуры, со­стоящие из катушки индуктивно­сти и конденсатора с малыми по­терями, приближающиеся по своим свойствам к идеальному параллельному LC-контуру. Бла­годаря свойству не пропускать резонансный ток параллельный LC-контур называют «фильтром – пробкой».

Коэффициентом мощно­сти называют отношение актив­ной мощности к полной. Из тре­угольника мощностей на рис. 3.15, а следует, что коэффи­циент мощности численно равен косинусу угла сдвига фаз φ ме­жду напряжением и током цепи .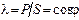

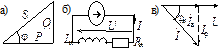
Рис. 3.15. Треугольник мощ­ностей (а), схема замещения фазы асинхронного дви-

гателя (б) и векторная диа­грамма для этой схемы (в)

Генераторы перемен­ного тока и трансформаторы про­ектируют на определенное номи­нальное напряжение U_ном, от ве­личины которого зависит степень изоляции, и на определенный но­минальный ток I_ном, задающий требуемое сечение проводов об­моток, т.е. эти устройства проек­тируют на номинальную полную мощность S_ном = U_номI_ном. При низком cosφ активная мощность P = S_номcosφ << S_ном, что свиде­тельствует о неполном использо­вании генератора, трансформато­ров, линии передачи. Экономиче­ски выгодно такое использование оборудования, при котором гене­ратор отдает в сеть активную мощность P, по величине при­ближающуюся к S_ном (P ≈ S_ном). Это означает, что значение коэф­фициента мощности должно быть близким к 1. Большинство про­мышленных потребителей элек­троэнергии для сети представляет активно – индуктивную нагрузку. На рис. 3.15, б показана схема за­мещения одной фазы асинхрон­ного двигателя. Из векторной диаграммы на рис. 3.15, в видно, что при низком cosφ_н (большом значении угла φ_н), ток I содержит значительную реактивную (ин­дуктивную) составляющую I_p = Isinφ_н, которая определяет ре­активную мощность Q = UIsinφ_н = UI_p. Для низкого cosφ_н в системе генератор – на­грузка существует интенсивный энергообмен между магнитным полем нагрузки и генератором. При этом обмотки генератора и трансформатора, а также распре­делительная сеть бесполезно за­гружены реактивным током I_р, что вызывает дополнительные потери.

Одним из способов сни­жения реактивного тока является параллельное подключение к на­грузке конденсатора (рис. 3.16, а). В большинстве случаев не требу­ется полная компенсация сдвига фаз. Достаточно, чтобы требуе­мый сдвиг фаз не превышал за­данного значения φ_тр. Как видно из рис. 3.16, б, подключение ем­кости C уменьшает ток генера­тора от значения 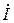до значения 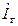, при этом сохраняется актив­ная составляющая I_а, а значит, и активная мощность нагрузки P = UIcosφ_н = UI_a. С помощью векторной диаграммы можно оп­ределить требуемое значение ем­кости:

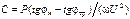. (3.73)

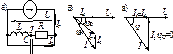
Рис. 3.16. Компенсация реактив­ной мощности при помощи до­полнительного конденсатора: а) схема; б) векторная диаграмма при неполной компенсации;

в) векторная диаграмма при пол­ной компенсации

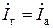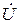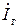При φ_тр = 0 (рис. 3.16, в) наблю­дается полная компенсация реак­тивного тока в генераторе и ли­нии передачи: I_р,тр; ;Q=0. Поскольку напря­жение и ток параллель­ного контура совпадают по фазе, то это означает, что режим пол­ной компенсации реактивной мощности является режимом ре­зонанса токов. При φ_тр = 0 фор­мулы (3.72) и (3.73) эквива­лентны. Уменьшение в результате компенсации тока генератора по­зволяет подключить к генератору дополнительную нагрузку и, тем самым, улучшить степень его пользования.

Повышение cosφ – важная народ­нохозяйственная задача. Для ее решения принимают различные меры организационного, техниче­ского и законодательного харак­тера. В последующих главах бу­дут затрагиваться вопросы повы­шения cosφ_н

18. Трехфазные элек­трические цепи. Прин­цип получения трех­фазного тока. Соедине­ние фазовых обмоток генератора звездой. Векторная диаграмма. ЭДС

Четырехпроводная сеть. На рис.4.5а изображена четырех­проводная цепь. Определим фаз­ные и линейные токи. Фазными называют токи, протекающие по фазам приемника и генератора. На рис.4.5а 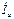, , 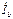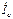– фазные токи. Токи, протекающие по ли­нейным проводам – линейные. На рис.4.5а токи 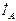, , 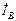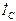– линей­ные токи. В цепи на рис.4.5а фазные и линейные токи равны: 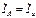, , 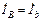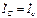. Это свойство нарушится, если, например, фазы приемника пере­соединить в треугольник или к линии подключить еще один при­емник.

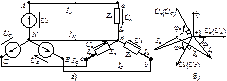
Рис. 4.5. Схема соединения звезда-звезда с нейтральным про­водом

Примем, что сопротив­лениями линии и нейтрального провода можно пренебречь. Тогда фазное напряжение 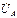генера­тора по двум проводам (линей­ному и нейтральному) приклады­вается непосредственно к Z_a, т.е. 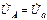. Для других фаз: 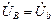, 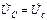. По закону Ома находим фазные токи при­емника:

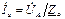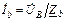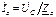; ; (4.5)

и по первому закону Кирхгофа для нейтрали n приемника полу­чаем

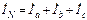. (4.6)

Пример. Пусть 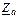=R_a+jX_La, φ_a>0; 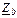=jX_Lb, φ_b=90°; 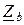=–jX_Cc, φ_c=–90°.

По формулам (4.5) рас­считываем фазные токи 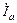, , 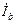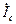и строим их векторы на диа­грамме (рис.4.5б). Векторы токов удобно строить «цепочкой», т.е. каждый новый вектор тока стро­ится на вершине предыдущего вектора. Тогда, соединив начало 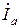с вершиной 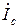, получим век­тор 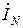тока в нейтрали. Фор­мулы (4.5), (4.6) верны для произ­вольного несимметричного трех­фазного приемника, в качестве которого могут выступать три от­дельных однофазных приемника (например, осветительная на­грузка). Для симметричного трехфазного приемника 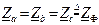(например, асинхронный двигатель)

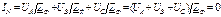. (4.7)

Равенство нулю обеспечивается тем, что векторы 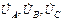симметричного генератора в сумме образуют нуль. Равенство нулю тока нейтрали говорит о том, что при симметричной на­грузке нейтральный провод лиш­ний. Поэтому для подключения асинхронных двигателей приме­няют трехпроводные линии. Важным достоинством четырех­проводной цепи является обеспе­чение независимой работы фаз нагрузки, т.е. изменение сопро­тивления одной фазы приемника не ведет к изменению напряже­ний других фаз нагрузки. Ней­тральный провод используют для несимметричной трехфазной на­грузки, причем в нейтральный провод не ставят отключающие автоматы или плавкие предохра­нители. Причина этого будет вы­яснена далее.

Трехпроводная сеть. Трехпроводная сеть используется для симметричных трехфазных приемников. Рассмотрим про­цессы в трехпроводной цепи при нагрузке «несимметричная звезда» (рис.4.6а).

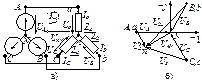
Рис. 4.6. Схема соединения звезда-звезда без нейтрального провода

В этой схеме потенциал точки n не задается генератором ( 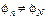), поэтому фазные на­пряжения нагрузки 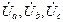неизвестны и их нужно рассчиты­вать. Схема содержит два узла (N и n), поэтому удобен метод двух узлов, в соответствии с которым

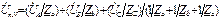(4.7)

или

,

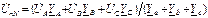где 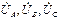– фазные напряже­ния генератора;

В трехфазных цепях напряжение 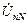называют напряжением смещения нейтрали. Применив ВЗК для обобщенного контура K_a (рис. 4.6а) и по аналогичным кон­турам, проходящим по фазам ис­точника и приемника и по напря­жению смещения нейтрали, полу­чим

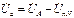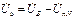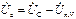; ; (4.8)

Токи фаз 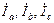находим по закону Ома:

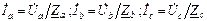. (4.9)

Стандартная методика расчета трехпроводной цепи с не­симметричной звездой выглядит так: 1) по (4.7) находят смещение нейтрали; 2) по (4.8) вычисляют фазные напряжения приемника; 3) по (4.9) определяет фазные токи приемника;4) целесообразно выполнить проверку по ПЗК: .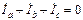

Смещение нейтрали получает наглядную графическую иллюстрацию на топографиче­ской диаграмме напряжений рас­сматриваемой цепи (рис.4.6б). Пусть точка N находится в начале координат. Напряжение 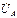имеет нулевую начальную фазу и на­правлено из А в N. Поэтому век­тор 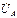на диаграмме горизонта­лен и направлен также из А в N. Вектор 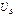должен быть направ­лен к N иотставать по фазе от 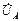на 120°. Аналогично строится вектор 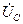, опережающий 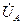на 120°. Переходим от 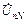к об­ратному вектору 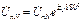и строим 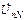из точки N. Вершина 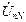дает точку n. В схеме фазное напряже­ние 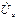направлено из точки а в точку n, поэтому на диаграмме строим 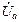, направляя его из точки а в точку n. Повторяем это построение для других фаз при­емника. Точка n на диаграмме смещена относительно N. Отсюда и появился термин «смещение нейтрали».

Топографическая диа­грамма демонстрирует, что из-за смещения нейтрали фазные на­пряжения приемника 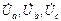резко несимметричны (у них раз­ные амплитуды и несимметрич­ные фазовые сдвиги). Это явле­ние называют перекосом фаз. Если сопротивление одной фазы изменить, то из (4.7) следует, что изменится смещение нейтрали 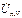, т.е. n изменит положение. Это влечет изменение напряже­ний всех фаз приемника. Ясно, что в четырехпроводной цепи при обрыве нейтрального провода для несимметричного трехфазного приемника немедленно устано­вится перекос фаз. У одних по­требителей будет опасное пере­напряжение, у других – резкое падение напряжения.

Из предыдущего пункта известно, что при симмет­ричной нагрузке напряжения фаз нагрузки симметричны незави­симо от наличия или отсутствия нейтрального провода. Покажем это иначе. Пусть приемник сим­метричен: 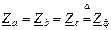. Тогда, вынося в (4.7) 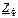за скобку, получим множитель ( 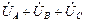), который для симметричного генератора равен нулю. При симметричной звезде смещение нейтрали отсутствует ( 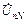=0), поэтому из (4.8) полу­чаем:

, , .

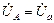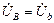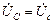Таким образом, в трехпроводной цепи с симметричной звездой фазные напряжения приемника симметричны и равны соответст­вующим фазным напряжениям генератора.

Из топографической диаграммы на рис.4.6б легко найти все напряжения цепи. На­пример, линейное напряжение 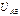определяется вектором, иду­щим из точки А в точку В и т.п.

Расчет сложной электрической цепи с помощью метода контурных токов. Пример расчета.

Если структура некоторого участка цепи, имеющего внешние зажимы, преобразована таким образом, чтобы токи всех внешних зажимов и напряжения между ними не изменились, то такое преобразование называют эквивалентным. Эквивалентным являлось преобразование реального источника ЭДС в реальный источник тока и обратно.

Последовательное соединение. Схема с последовательным соединением элементов приведена на рис. 2.3.

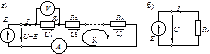
Рис. 2.3. Последовательное соединение: а) схема; б) эквивалентная схема

Пусть источник ЭДС идеален, т.е. U = E. Найдем эквивалентное сопротивление R_э, которым можно заменить все n последовательных элементов, так, чтобы ток I сохранился. Записываем ВЗК для обобщенного контура К: 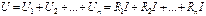. Откуда:

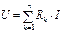. (2.1)

Для эквивалентной схемы на рис. 2.3, б, согласно закону Ома:

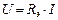. (2.2)

Сопоставив (2.1) и (2.2), получим:

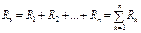. (2.3)

Таким образом, эквивалентное сопротивление последовательных R-элементов равно сумме их сопротивлений. Показание амперметра, измеряющего ток I в контуре I = U/R_э, а показание вольтметра, измеряющего напряжение U₁, по закону Ома U₁ = R₁I = UR₁/R_э. При последовательном соединении элементов напряжения на элементах распределяются пропорционально их сопротивлениям.

Параллельное соединение. Схема с параллельным соединением элементов приведена на рис. 2.4.

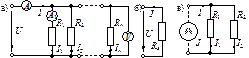
Рис. 2.4. Параллельное соединение элементов: а) схема; б) эквивалентная схема;

в) параллельное включение двух элементов

Схемы на рис. 2.4, а и рис. 2.4, б эквивалентные, т.е. входное напряжение U и входной ток I у них одинаковы. В схеме на рис. 2.4, а все проводники идеальные, поэтому напряжение на каждом R-элементе одинаково и равно U. Показание вольтметра также равно U. По закону Ома токи элементов: 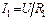; ;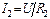…; ; 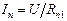и по первому закону Кирхгофа выражаем входной ток I:

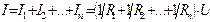. (2.4)

В эквивалентной цепи на рис. 2.4, б

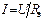. (2.5)

Сопоставив (2.4) и (2.5), получим:

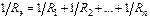. (2.6)

Вводя обозначения проводимостей (2.6) переписываем в виде:

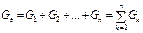. (2.7)

Таким образом, эквивалентная проводимость G_э параллельных R-элементов равна сумме их проводимостей. Эквивалентное сопротивление R_э равно 1/G_э. На практике распространен случай параллельного включения двух элементов (рис. 2.4, в). Для этой цепи из (2.6) следует

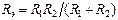. (2.8)

Из 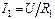; ; 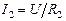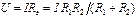получаем:

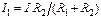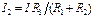; . (2.9)

Выражения (2.9) называют «правилом плеч». Они позволяют разбить известный ток I на два параллельных тока I₁, I₂, причем в качестве тока I может выступать ток J источника тока (рис. 2.4, в).

Смешанное соединение. Смешанным называют соединение, содержащее комбинацию последовательных и параллельных ветвей. Рассмотрим порядок расчета цепи со смешанным соединением на примере схемы, приведенной на рис. 2.5, а. В этой цепи заданы напряжение U источника ЭДС и сопротивления элементов. Требуется рассчитать эквивалентные сопротивления цепи и показания приборов.

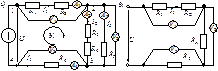
Рис. 2.5. Смешанное соединение элементов: а) схема; б) эквивалентная схема

Схема на рис. 2.5, а содержит три ветви: 1) ветвь I с током I₁, содержащую источник ЭДС с напряжением U и R-элементы R₁, R₂; 2) ветвь II с током I₂, содержащую R₃ и R₄; ветвь III с током I₃, состоящую из одного элемента R₅. Сопротивления ветвей равны: 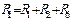; ; 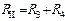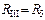. Ветви II и III включены параллельно, и их можно заменить (рис. 2.5, б) эквивалентной ветвью с сопротивлением R_э1: R_э1 = R_ΙΙR_ΙΙΙ/(R_ΙΙ + R_ΙΙΙ). В результате получим цепь на рис. 2.5, б, содержащую только последовательное соединение элементов, для которого R_э = R₁ + R₂ + R_э1 + R₆. Далее определяем ток I₁: I₁ = U/R_э. Амперметры А₁ и А₄ находятся в ветви I, поэтому их показания одинаковы и равны I₁. Токи I₂, I₃ определяем по «правилу плеч»: ;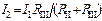