Графический метод с использованием характеристик для мгновенных значений
В общем случае методика анализа нелинейной цепи данным методом включает в себя следующие этапы:
-исходя из физических соображений находят (если он не задан) закон изменения одной из величин, определяющих характеристику  нелинейного элемента;
нелинейного элемента;
-по нелинейной характеристике  для известного закона изменения переменной
для известного закона изменения переменной 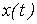 путем графических построений определяют кривую
путем графических построений определяют кривую  (или наоборот);
(или наоборот);
-с использованием полученной зависимости  проводят анализ остальной (линейной) части цепи.
проводят анализ остальной (линейной) части цепи.
В качестве примера построим при синусоидальной ЭДС  кривую тока в цепи на рис. 3, ВАХ
кривую тока в цепи на рис. 3, ВАХ  диода в которой представлена на рис. 4.
диода в которой представлена на рис. 4.
 |  |
| Рис.4 |
Решение
1. Строим результирующую ВАХ  цепи (см. рис. 4) согласно соотношению
цепи (см. рис. 4) согласно соотношению

2. Находя для различных значений  с использованием полученной кривой соответствующие им значения тока, строим по точкам (см. рис. 5) кривую искомой зависимости
с использованием полученной кривой соответствующие им значения тока, строим по точкам (см. рис. 5) кривую искомой зависимости 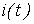 .
.
К полученному результату необходимо сделать следующий комментарий. Использование при анализе подобных цепей ВАХ идеального вентиля (обратный ток отсутствует, в проводящем направлении падение напряжения на диоде равно нулю) корректно при достаточно больших значениях амплитуд приложенного к диоду напряжения, определяющих значительное превышение током, протекающим через вентиль в прямом направлении, его обратного тока, вследствие чего последним можно пренебречь. При снижении величин напряжения, когда эти токи становятся сопоставимыми по величине, следует использовать ВАХ реального диода,представленную на рис. 4 и учитывающую наличие обратного тока.

Важнейшим элементом в цепях переменного тока является катушка с ферромагнитным сердечником. В общем случае кривая зависимости 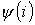 имеет вид гистерезисной петли, но, поскольку в устройствах, работающих при переменном напряжении, используются магнитные материалы с узкой петлей гистерезиса, в большинстве практических случаев допустимо при расчетах использовать основную (или начальную) кривую намагничивания.
имеет вид гистерезисной петли, но, поскольку в устройствах, работающих при переменном напряжении, используются магнитные материалы с узкой петлей гистерезиса, в большинстве практических случаев допустимо при расчетах использовать основную (или начальную) кривую намагничивания.
 Условное изображение нелинейной катушки индуктивности приведено на рис. 6. Здесь
Условное изображение нелинейной катушки индуктивности приведено на рис. 6. Здесь  – основной поток, замыкающийся по сердечнику,
– основной поток, замыкающийся по сердечнику,  - поток рассеяния, которому в первом приближении можно поставить в соответствие потокосцепление рассеяния
- поток рассеяния, которому в первом приближении можно поставить в соответствие потокосцепление рассеяния  , где индуктивность рассеяния
, где индуктивность рассеяния  в силу прохождения потоком
в силу прохождения потоком  части пути по воздуху.
части пути по воздуху.
Для схемы на рис. 6 справедливо уравнение
 , , | (1) |
где  .
.
В общем случае в силу нелинейности зависимости 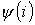 определить на основании (1) несинусоидальные зависимости
определить на основании (1) несинусоидальные зависимости 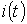 и
и  достаточно непросто. Вместе с тем для реальных катушек индуктивности падением напряжения
достаточно непросто. Вместе с тем для реальных катушек индуктивности падением напряжения  и ЭДС, обусловленной потоками рассеивания, вследствие их малости, часто можно пренебречь. При этом из (1) получаем
и ЭДС, обусловленной потоками рассеивания, вследствие их малости, часто можно пренебречь. При этом из (1) получаем  , откуда
, откуда
 ,
,
где  постоянная интегрирования.
постоянная интегрирования.
Так как характеристика 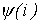 катушки (см. рис. 7) симметрична относительно начала координат, а напряжение
катушки (см. рис. 7) симметрична относительно начала координат, а напряжение  симметрично относительно оси абсцисс (оси времени), то кривая
симметрично относительно оси абсцисс (оси времени), то кривая 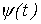 также должна быть симметричной относительно последней, откуда следует, что
также должна быть симметричной относительно последней, откуда следует, что  .
.

Находя для различных значений 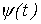 с использованием кривой
с использованием кривой 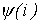 соответствующие им значения тока, строим по точкам (см. рис. 7) кривую зависимости
соответствующие им значения тока, строим по точкам (см. рис. 7) кривую зависимости  .
.
Анализ полученного результата позволяет сделать важный вывод: при синусоидальной форме потока напряжение  на катушке синусоидально, а протекающий через нее ток имеет явно выраженную несинусоидальную форму. Аналогично можно показать, что при синусоидальном токе поток, сцепленный с катушкой, и напряжение на ней несинусоидальны.
на катушке синусоидально, а протекающий через нее ток имеет явно выраженную несинусоидальную форму. Аналогично можно показать, что при синусоидальном токе поток, сцепленный с катушкой, и напряжение на ней несинусоидальны.
Для среднего значения напряжения, наведенного потоком, можно записать
 . . | (2) |
Умножив (2) на коэффициент формы, получим выражение для действующего значения напряжения
. 
В частности, если напряжение и поток синусоидальны, то
 .
.
Соотношение (2) является весьма важным: измеряя среднее значение напряжения, наведенного потоком, по (2) можно определить амплитуды потока  и индукции
и индукции  при любой форме нелинейности катушки.
при любой форме нелинейности катушки.
Аналогично проводится построение кривой  при синусоидальном потоке и задании зависимости
при синусоидальном потоке и задании зависимости 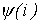 в виде петли гистерезиса. При этом следует помнить, что перемещение рабочей точки по петле осуществляется против часовой стрелки (см. рис. 8).
в виде петли гистерезиса. При этом следует помнить, что перемещение рабочей точки по петле осуществляется против часовой стрелки (см. рис. 8).

К полученному результату следует сделать следующий важный комментарий. Разложение построенной кривой  в ряд Фурье показывает, что первая гармоника тока (см. кривую
в ряд Фурье показывает, что первая гармоника тока (см. кривую  на рис. 8) опережает по фазе потокосцепление и, следовательно, отстает по фазе от синусоидального напряжения на катушке на угол, меньший 90°. Это указывает (
на рис. 8) опережает по фазе потокосцепление и, следовательно, отстает по фазе от синусоидального напряжения на катушке на угол, меньший 90°. Это указывает (  ) на потребление катушкой активной мощности, затрачиваемой на перемагничивание сердечника и определяемой площадью петли гистерезиса.
) на потребление катушкой активной мощности, затрачиваемой на перемагничивание сердечника и определяемой площадью петли гистерезиса.
Литература
- Основытеории цепей: Учеб. для вузов /Г.В.Зевеке, П.А.Ионкин, А.В.Нетушил, С.В.Страхов. –5-е изд., перераб. –М.: Энергоатомиздат, 1989. -528с.
- Бессонов Л.А.Теоретические основы электротехники: Электрические цепи. Учеб. для студентов электротехнических, энергетических и приборостроительных специальностей вузов. –7-е изд., перераб. и доп. –М.: Высш. шк., 1978. –528с.
- Теоретическиеосновы электротехники. Учеб. для вузов. В трех т. Под общ. ред. К.М.Поливанова. Т.2. Жуховицкий Б.Я., Негневицкий И.Б. Линейные электрические цепи (продолжение). Нелинейные цепи. –М.:Энергия- 1972. –200с.
Контрольные вопросы и задачи
- В чем заключаются особенности нелинейных цепей переменного тока?
- Какие типы характеристик используются в цепях переменного тока для описания нелинейных элементов?
- В каких случаях допустимо использование при расчетах идеальных ВАХ вентилей?
- Почему нельзя потокосцепление рассеяния катушки представить как произведение числа ее витков и потока рассеяния?
- Как косвенным путем можно определить амплитуду индукции магнитного поля, сцепленного с катушкой?
- Построить кривые
 и
и  при синусоидальном токе в нелинейной катушке.
при синусоидальном токе в нелинейной катушке. - Почему первая гармоника разложения кривой тока
 при учете гистерезисной петли отстает от напряжения на угол, меньший 90°?
при учете гистерезисной петли отстает от напряжения на угол, меньший 90°? - Определить амплитуду основного рабочего потока в сердечнике нелинейной катушки сечением
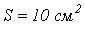 , если при числе витков
, если при числе витков  среднее значение напряжения, обусловленного изменением потока,
среднее значение напряжения, обусловленного изменением потока,  ; частота
; частота 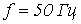 .
.
Ответ:  .
.
При анализе нелинейной цепи данным методом изменяющиеся по сложному закону переменные величины заменяются их первыми гармониками, что позволяет использовать векторные диаграммы. Основные этапы расчета: -строится график зависимости  нелинейного элемента для первых гармоник; -произвольно задаются амплитудой одной из переменных, например нелинейного элемента для первых гармоник; -произвольно задаются амплитудой одной из переменных, например  , связанной с нелинейным элементом, и по характеристике , связанной с нелинейным элементом, и по характеристике  последнего находят другую переменную последнего находят другую переменную  , определяющую режим работы нелинейного элемента, после чего, принимая все величины синусоидально изменяющимися во времени, на основании построения векторной диаграммы определяется амплитуда первой гармоники , определяющую режим работы нелинейного элемента, после чего, принимая все величины синусоидально изменяющимися во времени, на основании построения векторной диаграммы определяется амплитуда первой гармоники  переменной на входе цепи; -путем построения ряда векторных диаграмм для различных значений переменной на входе цепи; -путем построения ряда векторных диаграмм для различных значений  строится зависимость строится зависимость  , по которой для заданного значения , по которой для заданного значения  определяется действительная величина определяется действительная величина  , на основании чего проводится окончательный анализ цепи. Графический метод с использованием характеристик для действующих значений (метод эквивалентных синусоид) При анализе нелинейной цепи данным методом реальные несинусоидально изменяющиеся переменные заменяются эквивалентными им синусоидальными величинами, действующие значения которых равны действующим значениям исходных несинусоидальных переменных. Кроме того, активная мощность, определяемая с помощью эквивалентных синусоидальных величин, должна быть равна активной мощности в цепи с реальной (несинусоидальной) формой переменных. Используемый прием перехода к синусоидальным величинам определяет другое название метода - метод эквивалентных синусоид. Строго говоря, характеристика нелинейного элемента для действующих значений зависит от формы переменных, определяющих эту характеристику. Однако в первом приближении, особенно при качественном анализе, этим фактом обычно пренебрегают, считая характеристику неизменной для различных форм переменных. Указанное ограничивает возможности применения метода для цепей, где высшие гармоники играют существенную роль, например, для цепей с резонансными явлениями на высших гармониках. Переход к эквивалентным синусоидам позволяет использовать при анализе цепей векторные диаграммы. В связи с этим этапы расчета данным методом в общем случае совпадают с рассмотренными в предыдущем разделе. Метод расчета с использованием характеристик для действующих значений широко применяется для исследования явлений в цепях, содержащих нелинейную катушку индуктивности и линейный конденсатор (феррорезонансных цепях), или цепях с линейной катушкой индуктивности и нелинейным конденсатором. Кроме того, данный метод применяется для анализа цепей с инерционными нелинейными элементами, у которых постоянная времени, характеризующая их инерционные свойства, много больше периода переменного напряжения (тока) источника питания. В этом случае в установившихся режимах инерционные нелинейные элементы можно рассматривать как линейные с постоянными параметрами (сопротивлением, индуктивностью, емкостью). При этом сами параметры определяются по характеристикам нелинейных элементов для действующих значений и для различных величин последних являются разными. Феррорезонансные явления Различают феррорезонанс в последовательной цепи (феррорезонанс напряжений) и феррорезонанс в параллельной цепи (феррорезонанс токов). Рассмотрим первый из них на основе схемы на рис. 1. Для этого строим (см. рис. 2) прямую зависимости , на основании чего проводится окончательный анализ цепи. Графический метод с использованием характеристик для действующих значений (метод эквивалентных синусоид) При анализе нелинейной цепи данным методом реальные несинусоидально изменяющиеся переменные заменяются эквивалентными им синусоидальными величинами, действующие значения которых равны действующим значениям исходных несинусоидальных переменных. Кроме того, активная мощность, определяемая с помощью эквивалентных синусоидальных величин, должна быть равна активной мощности в цепи с реальной (несинусоидальной) формой переменных. Используемый прием перехода к синусоидальным величинам определяет другое название метода - метод эквивалентных синусоид. Строго говоря, характеристика нелинейного элемента для действующих значений зависит от формы переменных, определяющих эту характеристику. Однако в первом приближении, особенно при качественном анализе, этим фактом обычно пренебрегают, считая характеристику неизменной для различных форм переменных. Указанное ограничивает возможности применения метода для цепей, где высшие гармоники играют существенную роль, например, для цепей с резонансными явлениями на высших гармониках. Переход к эквивалентным синусоидам позволяет использовать при анализе цепей векторные диаграммы. В связи с этим этапы расчета данным методом в общем случае совпадают с рассмотренными в предыдущем разделе. Метод расчета с использованием характеристик для действующих значений широко применяется для исследования явлений в цепях, содержащих нелинейную катушку индуктивности и линейный конденсатор (феррорезонансных цепях), или цепях с линейной катушкой индуктивности и нелинейным конденсатором. Кроме того, данный метод применяется для анализа цепей с инерционными нелинейными элементами, у которых постоянная времени, характеризующая их инерционные свойства, много больше периода переменного напряжения (тока) источника питания. В этом случае в установившихся режимах инерционные нелинейные элементы можно рассматривать как линейные с постоянными параметрами (сопротивлением, индуктивностью, емкостью). При этом сами параметры определяются по характеристикам нелинейных элементов для действующих значений и для различных величин последних являются разными. Феррорезонансные явления Различают феррорезонанс в последовательной цепи (феррорезонанс напряжений) и феррорезонанс в параллельной цепи (феррорезонанс токов). Рассмотрим первый из них на основе схемы на рис. 1. Для этого строим (см. рис. 2) прямую зависимости  , определяемую соотношением , определяемую соотношением
Далее для двух значений сопротивлений Точка пересечения кривой Из построенных результирующих ВАХ цепи видно, что при увеличении питающего напряжения в цепи имеет место скачок тока: для кривой В соответствии с уравнением
на рис. 3 и 4 построены векторные диаграммы для двух произвольных значений тока (
Феррорезонанс в параллельной цепи рассмотрим на основе схемы на рис. 5. Для этого, как и в предыдущем случае, строим (см. рис. 6) прямую
Точка Из построенной ВАХ На рис. 7 для двух (до и после резонанса) значений напряжения (
Наши рекомендации |

 .
. 
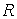 (
(  и
и  ) строим графики зависимостей
) строим графики зависимостей  : для
: для  (кривая
(кривая 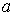 на рис. 2); для
на рис. 2); для  (кривая
(кривая  на рис. 2).
на рис. 2). с прямой
с прямой  , где
, где  -сопротивление, характеризующее потери в сердечнике, в режиме феррорезонанса
-сопротивление, характеризующее потери в сердечнике, в режиме феррорезонанса  не равно напряжению на конденсаторе.
не равно напряжению на конденсаторе.
 ) в режимах до и после резонанса для обеих ВАХ (для
) в режимах до и после резонанса для обеих ВАХ (для 
 , определяемую выражением (1).
, определяемую выражением (1).
 , в соответствии с соотношением
, в соответствии с соотношением  строим результирующую ВАХ
строим результирующую ВАХ  с прямой
с прямой  соответствует феррорезонансу токов. Необходимо отметить, что в реальном случае действительная ВАХ цепи в отличие от теоретической не касается оси ординат, что объясняется наличием высших гармоник тока и неидеальностью катушки индуктивности.
соответствует феррорезонансу токов. Необходимо отметить, что в реальном случае действительная ВАХ цепи в отличие от теоретической не касается оси ординат, что объясняется наличием высших гармоник тока и неидеальностью катушки индуктивности.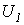 и
и  ) построены векторные диаграммы; при этом соответствующие выбранным напряжениям действующие значения токов
) построены векторные диаграммы; при этом соответствующие выбранным напряжениям действующие значения токов  и
и  взяты из графиков на рис. 6.
взяты из графиков на рис. 6.