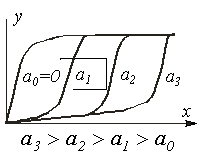Обратная” задача для неразветвленной магнитной цепи
Решение задач подобного типа осуществляется в следующей последовательности:
1. Задаются значениями потока и определяют для них НС 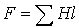 , как при решении “прямой” задачи. При этом следует стремиться подобрать два достаточно близких значения потока, чтобы получить
, как при решении “прямой” задачи. При этом следует стремиться подобрать два достаточно близких значения потока, чтобы получить 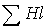 , несколько меньшую и несколько большую заданной величины НС.
, несколько меньшую и несколько большую заданной величины НС.
2. По полученным данным строится часть характеристики 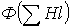 магнитной цепи (вблизи заданного значения НС), и по ней определяется поток, соответствующий заданной величине НС.
магнитной цепи (вблизи заданного значения НС), и по ней определяется поток, соответствующий заданной величине НС.
При расчете неразветвленных магнитных цепей, содержащих воздушные зазоры, удобно использовать метод пересечений, при котором искомое решение определяется точкой пересечения нелинейной вебер-амперной характеристики нелинейной части цепи и линейной характеристики линейного участка, строящейся на основании уравнения
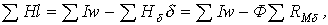
где 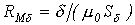 -магнитное сопротивление воздушного зазора.
-магнитное сопротивление воздушного зазора.
Обратная” задача для разветвленной магнитной цепи
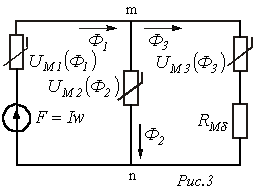 Замена магнитной цепи эквивалентной электрической схемой замещения (см. рис. 3, на котором приведена схема замещения магнитной цепи на рис. 2) позволяет решать задачи данного типа с использованием всех графических методов и приемов, применяемых при анализе аналогичных нелинейных электрических цепей постоянного тока.
Замена магнитной цепи эквивалентной электрической схемой замещения (см. рис. 3, на котором приведена схема замещения магнитной цепи на рис. 2) позволяет решать задачи данного типа с использованием всех графических методов и приемов, применяемых при анализе аналогичных нелинейных электрических цепей постоянного тока.
В этом случае при расчете магнитных цепей, содержащих два узла (такую конфигурацию имеет большое число используемых на практике магнитопроводов), широко используется метод двух узлов. Идея решения данным методом аналогична рассмотренной для нелинейных резистивных цепей постоянного тока и заключается в следующем:
1. Вычисляются зависимости 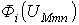 потоков во всех
потоков во всех 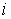 -х ветвях магнитной цепи в функции общей величины -магнитного напряжения
-х ветвях магнитной цепи в функции общей величины -магнитного напряжения 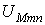 между узлами
между узлами 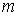 и
и 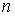 .
.
2. Определяется, в какой точке графически реализуется первый закон Кирхгофа 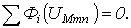 Соответствующие данной точке потоки являются решением задачи.
Соответствующие данной точке потоки являются решением задачи.
Итерационные методы расчета
Данные методы, сущность которых была рассмотрена при анализе нелинейных резистивных цепей постоянного тока, являются приближенными численными способами решения нелинейных алгебраических уравнений, описывающих состояние магнитной цепи. Как было отмечено выше, они хорошо поддаются машинной алгоритмизации и в настоящее время широко используются при исследовании сложных магнитных цепей на ЦВМ. При анализе относительно простых цепей, содержащих небольшое число узлов и нелинейных элементов в эквивалентной электрической схеме замещения (обычно до двух-трех), возможна реализация методов “вручную”.
В качестве примера приведем алгоритм расчета магнитной цепи на рис. 1, в которой при заданных геометрии магнитопровода, характеристике 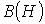 материала сердечника и величине НС F необходимо найти поток Ф.
материала сердечника и величине НС F необходимо найти поток Ф.
В соответствии с пошаговым расчетом для данной цепи можно записать
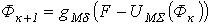 , , | (1) |
где 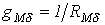 .
.
Задаемся значением 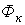 , вычисляем для
, вычисляем для 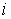 -х участков магнитопровода
-х участков магнитопровода 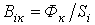 , по кривой намагничивания
, по кривой намагничивания 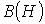 находим
находим 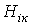 , подсчитываем
, подсчитываем 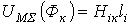 и по (1) определяем
и по (1) определяем 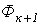 для следующего приближения и т.д., пока с заданной погрешностью не будет выполняться равенство
для следующего приближения и т.д., пока с заданной погрешностью не будет выполняться равенство 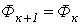 .
.
Статическая и дифференциальная индуктивности катушки
с ферромагнитным сердечником
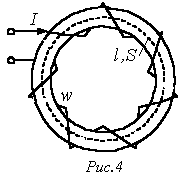
Пусть имеем катушку с ферромагнитным сердечником, представленную на рис. 4.
 В соответствии с определением потокосцепления
В соответствии с определением потокосцепления
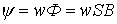 , , | (2) |
и на основании закона полного тока 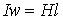 , откуда
, откуда
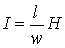 . . | (3) |
Из соотношений (2) и (3) вытекает, что функция 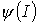 качественно имеет такой же вид, что и
качественно имеет такой же вид, что и 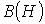 . Таким образом, зависимости относительной магнитной проницаемости
. Таким образом, зависимости относительной магнитной проницаемости 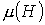 и индуктивности
и индуктивности 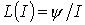 также подобны, т.е. представленные в предыдущей лекции на рис. 2 кривые
также подобны, т.е. представленные в предыдущей лекции на рис. 2 кривые 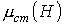 и
и 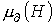 качественно аналогичны кривым
качественно аналогичны кривым 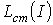 и
и 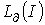 .
.
Статическая индуктивность катушки с ферромагнитным сердечником
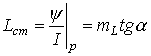 ;
;
дифференциальная индуктивность
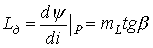 .
.
Если магнитную проводимость сердечника на рис. 4 обозначить через 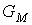 , то
, то 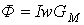 и
и 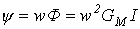 , откуда
, откуда
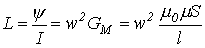 | (4) |
Используя соотношение (4), покажем влияние воздушного зазора на индуктивность катушки.
Пусть катушка на рис. 4 имеет воздушный зазор 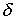 . Тогда полное магнитное сопротивление контура
. Тогда полное магнитное сопротивление контура
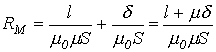 ,
,
откуда
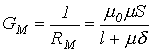 .
.
При 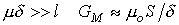 , следовательно
, следовательно
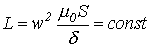 .
.
Таким образом, воздушный зазор линеаризует катушку с ферромагнитным сердечником. Зазор, для которого выполняется неравенство 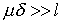 , называется большим зазором.
, называется большим зазором.
Литература
- Основытеории цепей: Учеб. для вузов /Г.В.Зевеке, П.А.Ионкин, А.В.Нетушил, С.В.Страхов. –5-е изд., перераб. –М.: Энергоатомиздат, 1989. -528с.
- Бессонов Л.А.Теоретические основы электротехники: Электрические цепи. Учеб. для студентов электротехнических, энергетических и приборостроительных специальностей вузов. –7-е изд., перераб. и доп. –М.: Высш. шк., 1978. –528с.
- Теоретическиеосновы электротехники. Учеб. для вузов. В трех т. Под общ. ред. К.М.Поливанова. Т.2. Жуховицкий Б.Я., Негневицкий И.Б. Линейные электрические цепи (продолжение). Нелинейные цепи. –М.:Энергия- 1972. –200с.
Контрольные вопросы и задачи
- Какие два типа задач встречаются при расчете магнитных цепей? Дайте им характеристику.
- Какие существуют методы расчета магнитных цепей?
- Какими методами решаются «обратные» задачи?
- Как влияет воздушный зазор на индуктивность нелинейной катушки?
- Что такое большой зазор?
- В магнитной цепи на рис. 2 заданы
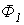 и
и 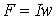 . Составить алгоритм расчета длины воздушного зазора
. Составить алгоритм расчета длины воздушного зазора 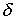 .
. - Составить алгоритм итерационного расчета потока в воздушном зазоре магнитной цепи на рис. 2 при заданной НС
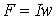 .
. - Запишите закон электромагнитной индукции с использованием статической
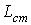 и дифференциальной
и дифференциальной 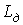 индуктивностей.
индуктивностей.
Особенности нелинейных цепей при переменных токах Наиболее существенная особенность расчета нелинейных цепей при переменных токах заключается в необходимости учета в общем случае динамических свойств нелинейных элементов, т.е. их анализ следует осуществлять на основе динамических вольт-амперных, вебер-амперных, и кулон-вольтных характеристик. Если нелинейный элемент является безынерционным, то его характеристики в динамических и статических режимах совпадают, что существенно упрощает расчет. Однако на практике идеально безынерционных элементов не существует. Отнесение нелинейного элемента к классу безынерционных определяется скоростью изменения входных воздействий: если период Т переменного воздействия достаточно мал по сравнению с постоянной времени  , характеризующей динамические свойства нелинейного элемента, последний рассматривается как безынерционный; если это не выполняется, то необходимо учитывать инерционные свойства нелинейного элемента. , характеризующей динамические свойства нелинейного элемента, последний рассматривается как безынерционный; если это не выполняется, то необходимо учитывать инерционные свойства нелинейного элемента. 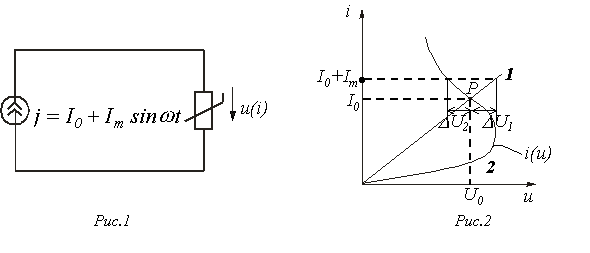 В качестве примера можно рассмотреть цепь на рис.1 с нелинейным резистором (термистором), имеющим вольт-амперную характеристику (ВАХ), представленную на рис. 2, и характеризующимся постоянной времени нагрева В качестве примера можно рассмотреть цепь на рис.1 с нелинейным резистором (термистором), имеющим вольт-амперную характеристику (ВАХ), представленную на рис. 2, и характеризующимся постоянной времени нагрева  . Если . Если 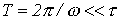 , то изображающая точка , то изображающая точка 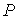 перемещается по прямой 1 и нелинейный резистор характеризуется сопротивлением перемещается по прямой 1 и нелинейный резистор характеризуется сопротивлением  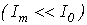 . При . При 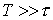 изображающая точка перемещается по кривой 2, и свойства нелинейного резистора определяются сопротивлением изображающая точка перемещается по кривой 2, и свойства нелинейного резистора определяются сопротивлением 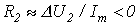 . Когда постоянная времени нагрева t НР одного порядка с Т, соотношения между переменными составляюшими напряжения и тока являются более сложными, определяющими сдвиг по фазе между ними. Другой важной особенностью нелинейных элементов в цепи переменного тока является вызываемое ими появление высших гармоник даже при наличии в цепи только источников синусоидального напряжения и (или) тока. На этом принципе строится, например, ряд умножителей частоты, а также преобразователей формы тока или напряжения. Основные типы характеристик нелинейных элементов в цепях переменного тока Использование динамических характеристик нелинейных элементов позволяет осуществлять расчет нелинейных цепей для мгновенных значений переменных, т.е. проводить принципиально ее наиболее точный и полный анализ. Однако в целом ряде случаев такой расчет может оказаться достаточно трудоемким или избыточным по своей глубине. Поэтому в зависимости от цели решаемой задачи, а также от требований к точности получаемых результатов, помимо динамической характеристики, могут использоваться нелинейные характеристики по первым гармоникам и для действующих значений (см. табл. 1). Таблица 1. Определение основных типов характеристик нелинейных элементов . Когда постоянная времени нагрева t НР одного порядка с Т, соотношения между переменными составляюшими напряжения и тока являются более сложными, определяющими сдвиг по фазе между ними. Другой важной особенностью нелинейных элементов в цепи переменного тока является вызываемое ими появление высших гармоник даже при наличии в цепи только источников синусоидального напряжения и (или) тока. На этом принципе строится, например, ряд умножителей частоты, а также преобразователей формы тока или напряжения. Основные типы характеристик нелинейных элементов в цепях переменного тока Использование динамических характеристик нелинейных элементов позволяет осуществлять расчет нелинейных цепей для мгновенных значений переменных, т.е. проводить принципиально ее наиболее точный и полный анализ. Однако в целом ряде случаев такой расчет может оказаться достаточно трудоемким или избыточным по своей глубине. Поэтому в зависимости от цели решаемой задачи, а также от требований к точности получаемых результатов, помимо динамической характеристики, могут использоваться нелинейные характеристики по первым гармоникам и для действующих значений (см. табл. 1). Таблица 1. Определение основных типов характеристик нелинейных элементов
Графические методы расчета Графические методы расчета позволяют проводить анализ нелинейных цепей переменного тока для частных значений параметров с использованием характеристик нелинейных элементов для мгновенных значений, по первым гармоникам и действующим значениям (см. табл. 1). Наши рекомендации |