Основные законы магнитных цепей
В основе расчета магнитных цепей лежат два закона (см. табл. 4).
Таблица 4.. Основные законы магнитной цепи
| Наименование закона | Аналитическое выражение закона | Формулировка закона |
| Закон (принцип) непрерывности магнитного потока | 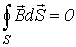 | Поток вектора магнитной индукции через замкнутую поверхность равен нулю |
| Закон полного тока | 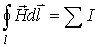 | Циркуляция вектора напряженности вдоль произвольного контура равна алгебраической сумме токов, охватываемых этим контуром |
При анализе магнитных цепей и, в первую очередь, при их синтезе обычно используют следующие допущения:
- магнитная напряженность, соответственно магнитная индукция, во всех точках поперечного сечения магнитопровода одинакова 
- потоки рассеяния отсутствуют (магнитный поток через любое сечение неразветвленной части магнитопровода одинаков);
- сечение воздушного зазора равно сечению прилегающих участков магнитопровода.
Это позволяет использовать при расчетах законы Кирхгофа и Ома для магнитных цепей (см. табл. 5), вытекающие из законов, сформулированных в табл. 4.
Таблица 5. Законы Кирхгофа и Ома для магнитных цепей
| Наименование закона | Аналитическое выражение закона | Формулировка закона |
| Первый закон Кирхгофа | 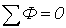 | Алгебраическая сумма магнитных потоков в узле магнитопровода равна нулю |
| Второй закон Кирхгофа | 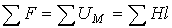 | Алгебраическая сумма падений магнитного напряжения вдоль замкнутого контура равна алгебраической сумме МДС, действующих в контуре |
| Закон Ома | 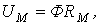 где где 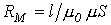 | Падение магнитного напряжения на участке магнитопровода длиной 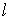 равно произведению магнитного потока и магнитного сопротивления равно произведению магнитного потока и магнитного сопротивления 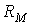 участка участка |
Сформулированные законы и понятия магнитных цепей позволяют провести формальную аналогию между основными величинами и законами, соответствующими электрическим и магнитным цепям, которую иллюстрирует табл. 6.
Таблица 6.Аналогия величин и законов для электрических и магнитных цепей
| Электрическая цепь | Магнитная цепь |
Ток 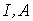 | Поток 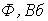 |
ЭДС 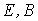 | МДС (НС) 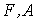 |
Электрическое сопротивление 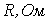 | Магнитное сопротивление 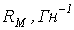 |
Электрическое напряжение 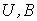 | Магнитное напряжение 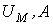 |
Первый закон Кирхгофа: 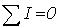 | Первый закон Кирхгофа: 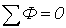 |
Второй закон Кирхгофа: 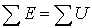 | Второй закон Кирхгофа: 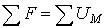 |
Закон Ома: 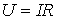 | Закон Ома: 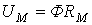 |
Литература
- Основытеории цепей: Учеб. для вузов /Г.В.Зевеке, П.А.Ионкин, А.В.Нетушил, С.В.Страхов. –5-е изд., перераб. –М.: Энергоатомиздат, 1989. -528с.
- Бессонов Л.А.Теоретические основы электротехники: Электрические цепи. Учеб. для студентов электротехнических, энергетических и приборостроительных специальностей вузов. –7-е изд., перераб. и доп. –М.: Высш. шк., 1978. –528с.
- Теоретическиеосновы электротехники. Учеб. для вузов. В трех т. Под общ. ред. К.М.Поливанова. Т.2. Жуховицкий Б.Я., Негневицкий И.Б. Линейные электрические цепи (продолжение). Нелинейные цепи. –М.:Энергия- 1972. –200с.
Контрольные вопросы и задачи
- Какие векторные величины характеризуют магнитное поле?
- Какие основные понятия связаны с петлей гистерезиса?
- Что характеризует площадь гистерезисной петли?
- Какие ферромагнитные материалы и почему используются для изготовления сердечников для машин переменного тока?
- Назовите основные законы магнитного поля?
- В чем заключаются основные допущения, принимаемые при расчете магнитных цепей?
- Проведите аналогию между электрическими и магнитными цепями?
- Магнитная индукция в сердечнике при напряженности Н=200 А/м составляет В=1,0 Тл. Определить относительную магнитную проницаемость.
Ответ: 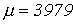 .
.
- Определить магнитное сопротивление участка цепи длиной
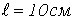 и сечением
и сечением 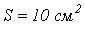 , если
, если 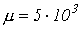 .
.
Ответ: 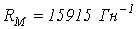 .
.
- В условиях предыдущей задачи определить падение магнитного напряжения на участке, если индукция В=0,8 Тл.
Ответ: 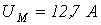 .
.
Указанная в предыдущей лекции формальная аналогия между электрическими и магнитными цепями позволяет распространить все методы и технику расчета нелинейных резистивных цепей постоянного тока на нелинейные магнитные цепи. При этом для наглядности можно составить эквивалентную электрическую схему замещенияисходной магнитной цепи, с использованием которой выполняется расчет. Нелинейность магнитных цепей определяется нелинейным характером зависимости 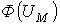 , являющейся аналогом ВАХ , являющейся аналогом ВАХ 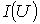 и определяемой характеристикой ферромагнитного материала и определяемой характеристикой ферромагнитного материала 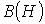 . При расчете магнитных цепей при постоянных потоках обычно используют основную кривую намагничивания. Петлеобразный характер зависимости . При расчете магнитных цепей при постоянных потоках обычно используют основную кривую намагничивания. Петлеобразный характер зависимости 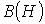 учитывается при расчете постоянных магнитов и электротехнических устройств на их основе. При расчете магнитных цепей на практике встречаются две типичные задачи: -задача определения величины намагничивающей силы (НС), необходимой для создания заданного магнитного потока (заданной магнитной индукции) на каком - либо участке магнитопровода (задача синтезаили“прямая“ задача); -задача нахождения потоков (магнитных индукций) на отдельных участках цепи по заданным значениям НС (задача анализаили “обратная” задача). Следует отметить, что задачи второго типа являются обычно более сложными и трудоемкими в решении. В общем случае в зависимости от типа решаемой задачи (“прямой” или “обратной”) решение может быть осуществлено следующими методами: -регулярными; -графическими; -итерационными. При этом при использовании каждого из этих методов первоначально необходимо указать на схеме направления НС, если известны направления токов в обмотках, или задаться их положительными направлениями, если их нужно определить. Затем задаются положительными направлениями магнитных потоков, после чего можно переходить к составлению эквивалентной схемы замещения и расчетам. Магнитные цепи по своей конфигурации могут быть подразделены на неразветвленныеи разветвленные.В неразветвленной магнитной цепи на всех ее участках имеет место один и тот же поток, т.е. различные участки цепи соединены между собой последовательно. Разветвленные магнитные цепи содержат два и более контура. Регулярные методы расчета Данными методами решаются задачи первого типа -”прямые” задачи. При этом в качестве исходных данных для расчета заданы конфигурация и основные геометрические размеры магнитной цепи, кривая (кривые) намагничивания ферромагнитного материала и магнитный поток или магнитная индукция в каком-либо сечении магнитопровода. Требуется найти НС, токи обмоток или, при известных значениях последних, число витков. 1. Прямая” задача для неразветвленной магнитной цепи Решение задач подобного типа осуществляется в следующей последовательности: 1. Намечается средняя линия (см. пунктирную линию на рис.1), которая затем делится на участки с одинаковым сечением магнитопровода. 2. Исходя из постоянства магнитного потока вдоль всей цепи, определяются значения индукции для каждого учитывается при расчете постоянных магнитов и электротехнических устройств на их основе. При расчете магнитных цепей на практике встречаются две типичные задачи: -задача определения величины намагничивающей силы (НС), необходимой для создания заданного магнитного потока (заданной магнитной индукции) на каком - либо участке магнитопровода (задача синтезаили“прямая“ задача); -задача нахождения потоков (магнитных индукций) на отдельных участках цепи по заданным значениям НС (задача анализаили “обратная” задача). Следует отметить, что задачи второго типа являются обычно более сложными и трудоемкими в решении. В общем случае в зависимости от типа решаемой задачи (“прямой” или “обратной”) решение может быть осуществлено следующими методами: -регулярными; -графическими; -итерационными. При этом при использовании каждого из этих методов первоначально необходимо указать на схеме направления НС, если известны направления токов в обмотках, или задаться их положительными направлениями, если их нужно определить. Затем задаются положительными направлениями магнитных потоков, после чего можно переходить к составлению эквивалентной схемы замещения и расчетам. Магнитные цепи по своей конфигурации могут быть подразделены на неразветвленныеи разветвленные.В неразветвленной магнитной цепи на всех ее участках имеет место один и тот же поток, т.е. различные участки цепи соединены между собой последовательно. Разветвленные магнитные цепи содержат два и более контура. Регулярные методы расчета Данными методами решаются задачи первого типа -”прямые” задачи. При этом в качестве исходных данных для расчета заданы конфигурация и основные геометрические размеры магнитной цепи, кривая (кривые) намагничивания ферромагнитного материала и магнитный поток или магнитная индукция в каком-либо сечении магнитопровода. Требуется найти НС, токи обмоток или, при известных значениях последних, число витков. 1. Прямая” задача для неразветвленной магнитной цепи Решение задач подобного типа осуществляется в следующей последовательности: 1. Намечается средняя линия (см. пунктирную линию на рис.1), которая затем делится на участки с одинаковым сечением магнитопровода. 2. Исходя из постоянства магнитного потока вдоль всей цепи, определяются значения индукции для каждого  -го участка: -го участка: 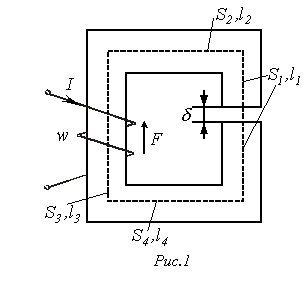 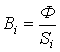 . 3. По кривой намагничивания для каждого значения . 3. По кривой намагничивания для каждого значения 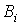 находятся напряженности находятся напряженности 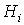 на ферромагнитных участках; напряженность поля в воздушном зазоре определяется согласно на ферромагнитных участках; напряженность поля в воздушном зазоре определяется согласно 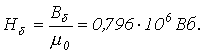 4. По второму закону Кирхгофа для магнитной цепи определяется искомая НС путем суммирования падений магнитного напряжения вдоль контура: 4. По второму закону Кирхгофа для магнитной цепи определяется искомая НС путем суммирования падений магнитного напряжения вдоль контура: 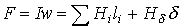 , где , где 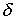 -длина воздушного зазора. 2. “Прямая” задача для разветвленной магнитной цепи Расчет разветвленных магнитных цепей основан на совместном применении первого и второго законов Кирхгофа для магнитных цепей. Последовательность решения задач данного типа в целом соответствует рассмотренному выше алгоритму решения “прямой” задачи для неразветвленной цепи. При этом для определения магнитных потоков на участках магнитопровода, для которых магнитная напряженность известна или может быть вычислена на основании второго закона Кирхгофа, следует использовать алгоритм -длина воздушного зазора. 2. “Прямая” задача для разветвленной магнитной цепи Расчет разветвленных магнитных цепей основан на совместном применении первого и второго законов Кирхгофа для магнитных цепей. Последовательность решения задач данного типа в целом соответствует рассмотренному выше алгоритму решения “прямой” задачи для неразветвленной цепи. При этом для определения магнитных потоков на участках магнитопровода, для которых магнитная напряженность известна или может быть вычислена на основании второго закона Кирхгофа, следует использовать алгоритм
В остальных случаях неизвестные магнитные потоки определяются на основании первого закона Кирхгофа для магнитных цепей.
Алгоритм решения задачи следующий: 1. Задаем положительные направления магнитных потоков в стержнях магнитопровода (см. рис. 2). 2. Определяем напряженность в воздушном зазоре 3. По второму закону Кирхгофа для правого контура можно записать
откуда находим 4. В соответствии с первым законом Кирхгофа
Тогда 5. В соответствии со вторым законом Кирхгофа для искомой НС имеет место уравнение
Графические методы расчета Графическими методами решаются задачи второго типа - “обратные” задачи. При этом в качестве исходных данных для расчета заданы конфигурация и геометрические размеры магнитной цепи, кривая (кривые) намагничивания ферромагнитного материала, а также НС обмоток. Требуется найти значения потоков (индукций) на отдельных участках магнитопровода. Данные методы основаны на графическом представлении вебер-амперных характеристик Наши рекомендации
|

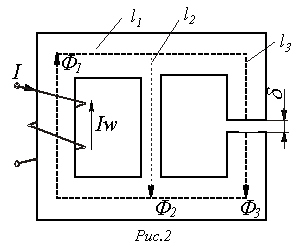 В качестве примера анализа разветвленной магнитной цепи при заданных геометрии магнитной цепи на рис. 2 и характеристике
В качестве примера анализа разветвленной магнитной цепи при заданных геометрии магнитной цепи на рис. 2 и характеристике 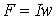 , необходимую для создания в воздушном зазоре индукции
, необходимую для создания в воздушном зазоре индукции 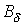 .
.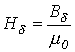 и по зависимости
и по зависимости 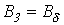 - значение
- значение 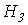 .
.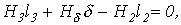
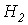 и по зависимости
и по зависимости 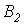 .
.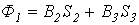 .
.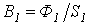 , и по зависимости
, и по зависимости 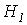 .
.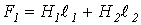 .
.