Резистор (идеальное активное сопротивление).

Здесь напряжение и ток (см. рис. 2) совпадают по фазе  , поэтому мощность
, поэтому мощность  всегда положительна, т.е. резистор потребляет активную мощность
всегда положительна, т.е. резистор потребляет активную мощность

Катушка индуктивности (идеальная индуктивность)

При идеальной индуктивности ток отстает от напряжения по фазе на  . Поэтому в соответствии с (3) можно записать
. Поэтому в соответствии с (3) можно записать  .
.
Участок 1-2: энергия  , запасаемая в магнитном поле катушки, нарастает.
, запасаемая в магнитном поле катушки, нарастает.
Участок 2-3: энергия магнитного поля убывает, возвращаясь в источник.
Конденсатор (идеальная емкость)
Аналогичный характер имеют процессы и для идеальной емкости. Здесь  . Поэтому из (3) вытекает, что
. Поэтому из (3) вытекает, что  . Таким образом, в катушке индуктивности и конденсаторе активная мощность не потребляется (Р=0), так как в них не происходит необратимого преобразования энергии в другие виды энергии. Здесь происходит только циркуляция энергии: электрическая энергия запасается в магнитном поле катушки или электрическом поле конденсатора на протяжении четверти периода, а на протяжении следующей четверти периода энергия вновь возвращается в сеть. В силу этого катушку индуктивности и конденсатор называют реактивными элементами, а их сопротивления ХL и ХС , в отличие от активного сопротивления R резистора, – реактивными.
. Таким образом, в катушке индуктивности и конденсаторе активная мощность не потребляется (Р=0), так как в них не происходит необратимого преобразования энергии в другие виды энергии. Здесь происходит только циркуляция энергии: электрическая энергия запасается в магнитном поле катушки или электрическом поле конденсатора на протяжении четверти периода, а на протяжении следующей четверти периода энергия вновь возвращается в сеть. В силу этого катушку индуктивности и конденсатор называют реактивными элементами, а их сопротивления ХL и ХС , в отличие от активного сопротивления R резистора, – реактивными.
Интенсивность обмена энергии принято характеризовать наибольшим значением скорости поступления энергии в магнитное поле катушки или электрическое поле конденсатора, которое называется реактивной мощностью.
В общем случае выражение для реактивной мощности имеет вид:
 | (5) |
Она положительна при отстающем токе (индуктивная нагрузка-  ) и отрицательна при опережающем токе (емкостная нагрузка-
) и отрицательна при опережающем токе (емкостная нагрузка-  ). Единицу мощности в применении к измерению реактивной мощности называют вольт-ампер реактивный (ВАр).
). Единицу мощности в применении к измерению реактивной мощности называют вольт-ампер реактивный (ВАр).
В частности для катушки индуктивности имеем:
 , так как
, так как  .
.
 .
.
Из последнего видно, что реактивная мощность для идеальной катушки индуктивности пропорциональна частоте и максимальному запасу энергии в катушке. Аналогично можно получить для идеального конденсатора:
 .
.
Полная мощность
Помимо понятий активной и реактивной мощностей в электротехнике широко используется понятие полной мощности:
 . . | (6) |
Активная, реактивная и полная мощности связаны следующим соотношением:
 . . | (7) |
Отношение активной мощности к полной называют коэффициентом мощности. Из приведенных выше соотношений видно, что коэффициент мощности  равен косинусу угла сдвига между током и напряжением. Итак,
равен косинусу угла сдвига между током и напряжением. Итак,
 . . | (8) |
Комплексная мощность
Активную, реактивную и полную мощности можно определить, пользуясь комплексными изображениями напряжения и тока. Пусть  , а
, а  . Тогда комплекс полной мощности:
. Тогда комплекс полной мощности:
 , , | (9) |
где  - комплекс, сопряженный с комплексом
- комплекс, сопряженный с комплексом 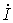 .
.
 .
.
 Комплексной мощности можно поставить в соответствие треугольник мощностей (см. рис. 4). Рис. 4 соответствует
Комплексной мощности можно поставить в соответствие треугольник мощностей (см. рис. 4). Рис. 4 соответствует  (активно-индуктивная нагрузка), для которого имеем:
(активно-индуктивная нагрузка), для которого имеем:
.
Применение статических конденсаторов для повышения cos 
Как уже указывалось, реактивная мощность  циркулирует между источником и потребителем. Реактивный ток, не совершая полезной работы, приводит к дополнительным потерям в силовом оборудовании и, следовательно, к завышению его установленной мощности. В этой связи понятно стремление к увеличению
циркулирует между источником и потребителем. Реактивный ток, не совершая полезной работы, приводит к дополнительным потерям в силовом оборудовании и, следовательно, к завышению его установленной мощности. В этой связи понятно стремление к увеличению  в силовых электрических цепях.
в силовых электрических цепях.
Следует указать, что подавляющее большинство потребителей (электродвигатели, электрические печи, другие различные устройства и приборы) как нагрузка носит активно-индуктивный характер.

Если параллельно такой нагрузке  (см. рис. 5), включить конденсатор С, то общий ток
(см. рис. 5), включить конденсатор С, то общий ток 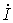 , как видно из векторной диаграммы (рис. 6), приближается по фазе к напряжению, т.е.
, как видно из векторной диаграммы (рис. 6), приближается по фазе к напряжению, т.е.  увеличивается, а общая величина тока (а следовательно, потери) уменьшается при постоянстве активной мощности
увеличивается, а общая величина тока (а следовательно, потери) уменьшается при постоянстве активной мощности  . На этом основано применение конденсаторов для повышения
. На этом основано применение конденсаторов для повышения  .
.
Какую емкость С нужно взять, чтобы повысить коэффициент мощности от значения  до значения
до значения  ?
?
Разложим  на активную
на активную  и реактивную
и реактивную  составляющие. Ток через конденсатор
составляющие. Ток через конденсатор  компенсирует часть реактивной составляющей тока нагрузки
компенсирует часть реактивной составляющей тока нагрузки  :
:
 ; ; | (10) |
 ; ; | (11) |
 . . | (12) |
Из (11) и (12) с учетом (10) имеем
 ,
,
но  , откуда необходимая для повышения
, откуда необходимая для повышения  емкость:
емкость:
 . . | (13) |
Баланс мощностей
Баланс мощностей является следствием закона сохранения энергии и может служить критерием правильности расчета электрической цепи.
а) Постоянный ток
Для любой цепи постоянного тока выполняется соотношение:
 | (14) |
Это уравнение представляет собой математическую форму записи баланса мощностей: суммарная мощность, генерируемая источниками электрической энергии, равна суммарной мощности, потребляемой в цепи.
Следует указать, что в левой части (14) слагаемые имеют знак “+”, поскольку активная мощность рассеивается на резисторах. В правой части (14) сумма слагаемых больше нуля, но отдельные члены здесь могут иметь знак “-”, что говорит о том, что соответствующие источники работают в режиме потребителей энергии (например, заряд аккумулятора).
б) Переменный ток.
Из закона сохранения энергии следует, что сумма всех отдаваемых активных мощностей равна сумме всех потребляемых активных мощностей, т.е.
 | (15) |
В ТОЭ доказывается (вследствие достаточной громоздкости вывода это доказательство опустим), что баланс соблюдается и для реактивных мощностей:
 , , | (16) |
где знак “+” относится к индуктивным элементам  , “-” – к емкостным
, “-” – к емкостным  .
.
Умножив (16) на “j” и сложив полученный результат с (15), придем к аналитическому выражению баланса мощностей в цепях синусоидального тока (без учета взаимной индуктивности):

или
 .
.
Литература
- Основы теории цепей: Учеб. для вузов /Г.В.Зевеке, П.А.Ионкин, А.В.Нетушил, С.В.Страхов. –5-е изд., перераб. –М.: Энергоатомиздат, 1989. -528с.
- Бессонов Л.А. Теоретические основы электротехники: Электрические цепи. Учеб. для студентов электротехнических, энергетических и приборостроительных специальностей вузов. –7-е изд., перераб. и доп. –М.: Высш. шк., 1978. –528с.
Контрольные вопросы и задачи
- Что такое активная мощность?
- Что такое реактивная мощность, с какими элементами она связана?
- Что такое полная мощность?
- Почему необходимо стремиться к повышению коэффициента мощности
 ?
? - Критерием чего служит баланс мощностей?
- К источнику с напряжением
 подключена активно-индуктивная нагрузка, ток в которой
подключена активно-индуктивная нагрузка, ток в которой  . Определить активную, реактивную и полную мощности.
. Определить активную, реактивную и полную мощности.
Ответ: Р=250 Вт; Q=433 ВАр; S=500 ВА.
- В ветви, содержащей последовательно соединенные резистор R и катушку индуктивности L, ток I=2 A. Напряжение на зажимах ветви U=100 B, а потребляемая мощность Р=120 Вт. Определить сопротивления R и XL элементов ветви.
Ответ: R=30 Ом; XL=40 Ом.
- Мощность, потребляемая цепью, состоящей из параллельно соединенных конденсатора и резистора, Р=90 Вт. Ток в неразветвленной части цепи I1=5 A, а в ветви с резистором I2=4 A. Определить сопротивления R и XL элементов цепи.
Ответ: R=10 Ом; XС=7,5 Ом.
Резонансом называется такой режим работы цепи, включающей в себя индуктивные и емкостные элементы, при котором ее входное сопротивление (входная проводимость) вещественно. Следствием этого является совпадение по фазе тока на входе цепи с входным напряжением. Резонанс в цепи с последовательно соединенными элементами (резонанс напряжений)  Для цепи на рис.1 имеет место Для цепи на рис.1 имеет место  где где
В зависимости от соотношения величин 1. В цепи преобладает индуктивность, т.е.
2. В цепи преобладает емкость, т.е. 3. Условие резонанса напряжений
При этом, как следует из (1) и (2), При резонансе напряжений или режимах, близких к нему, ток в цепи резко возрастает. В теоретическом случае при R=0 его величина стремится к бесконечности. Соответственно возрастанию тока увеличиваются напряжения на индуктивном и емкостном элементах, которые могут во много раз превысить величину напряжения источника питания. Пусть, например, в цепи на рис. 1 Явление резонанса находит полезное применение на практике, в частности в радиотехнике. Однако, если он возникает стихийно, то может привести к аварийным режимам вследствие появления больших перенапряжений и сверхтоков. Физическая сущность резонанса заключается в периодическом обмене энергией между магнитным полем катушки индуктивности и электрическим полем конденсатора, причем сумма энергий полей остается постоянной. Суть дела не меняется, если в цепи имеется несколько индуктивных и емкостных элементов. Действительно, в этом случае Как показывает анализ уравнения (3), режима резонанса можно добиться путем изменения параметров L и C, а также частоты. На основании (3) для резонансной частоты можно записать
Резонансными кривыми называются зависимости тока и напряжения от частоты. В качестве их примера на рис. 3 приведены типовые кривые I(f); Важной характеристикой резонансного контура является добротность Q, определяемая отношением напряжения на индуктивном (емкостном) элементе к входному напряжению:
- и характеризующая “избирательные” свойства резонансного контура, в частности его полосу пропускания Другим параметром резонансного контура является характеристическое сопротивление, связанное с добротностью соотношением
или с учетом (4) и (5) для
Резонанс в цепи с параллельно соединенными элементами
где
В зависимости от соотношения величин
В цепи преобладает индуктивность, т.е. В цепи преобладает емкость, т.е.
Условие резонанса токов
При этом, как следует из (8) и (9), Идентичность соотношений (3) и (5) указывает, что в обоих случаях резонансная частота определяется соотношением (4). Однако не следует использовать выражение (4) для любой резонансной цепи. Оно справедливо только для простейших схем с последовательным или параллельным соединением индуктивного и емкостного элементов. При определении резонансной частоты в цепи произвольной конфигурации или, в общем случае, соотношения параметров схемы в режиме резонанса следует исходить из условия вещественности входного сопротивления (входной проводимости) цепи.
Поскольку в режиме резонанса мнимая часть
откуда, в частности, находится резонансная частота. Резонанс в сложной цепи Условие резонанса для сложной цепи со смешанным соединением нескольких индуктивных и емкостных элементов, заключающееся в равенстве нулю мнимой части входного сопротивления При определении резонансных частот для реактивного двухполюсника аналитическое выражение его входного реактивного сопротивления В качестве примера определим резонансные частоты для цепи рис. 7. Выражение входного сопротивления данной цепи имеет вид
Литература
Контрольные вопросы и задачи
Ответ:
Ответ: | ||||||||||||||||||||
| Лекция N 9. Векторные и топографические диаграммы. |
| Совокупность радиус-векторов, изображающих синусоидально изменяющиеся ЭДС, напряжения, токи и т. д., называется векторной диаграммой. Векторные диаграммы наглядно иллюстрируют ход решения задачи. При точном построении векторов можно непосредственно из диаграммы определить амплитуды и фазы искомых величин. Приближенное (качественное) построение диаграмм при аналитическом решении служит надежным контролем корректности хода решения и позволяет легко определить квадрант, в котором находятся определяемые векторы. При построении векторных диаграмм для цепей с последовательным соединением элементов за базовый (отправной) вектор следует принимать вектор тока (см. лекцию № 8), а к нему под соответствующими углами подстраивать векторы напряжений на отдельных элементах. Для цепей с параллельным соединением элементов за базовый (отправной) вектор следует принять вектор напряжения (см. лекцию № 8), ориентируя относительно него векторы токов в параллельных ветвях. Для наглядного определения величины и фазы напряжения между различными точками электрической цепи удобно использовать топографические диаграммы. Они представляют собой соединенные соответственно схеме электрической цепи точки на комплексной плоскости, отображающие их потенциалы. На топографической диаграмме, представляющей собой в принципе векторную диаграмму, порядок расположения векторов напряжений строго соответствует порядку расположения элементов в схеме, а вектор падения напряжения на каждом последующем элементе примыкает к концу вектора напряжения на каждом предыдущем элементе. В качестве примера построим векторную диаграмму токов, а также топографическую диаграмму потенциалов для схемы, расчет которой был приведен в лекции № 5 (см. рис. 1).
При данных параметрах и заданном напряжении на входе схемы При построении векторной диаграммы зададимся масштабами токов и напряжений (см. рис. 2). Векторную диаграмму можно строить, имея запись комплекса в показательной форме, т.е. по значениям модуля и фазы . Однако на практике удобнее проводить построения, используя алгебраическую форму записи, поскольку при этом вещественная и мнимая составляющие комплексной величины непосредственно откладываются на соответствующих осях комплексной плоскости, определяя положение точки на ней. Построение векторной диаграммы токов осуществляется непосредственно на основании известных значений их комплексов. Для построения топографической диаграммы предварительно осуществим расчет комплексных потенциалов (другой вариант построения топографической диаграммы предполагает расчет комплексов напряжений на элементах цепи с последующим суммированием векторов напряжений вдоль контура непосредственно на комплексной плоскости). При построении топографической диаграммы обход контуров можно производить по направлению тока или против. Чаще используют второй вариант.
В этом случае с учетом того, что в электротехнике принято, что ток течет от большего потенциала к меньшему, потенциал искомой точки равен потенциалу предыдущей плюс падение напряжения на элементе между этими точками. Если на пути обхода встречается источник ЭДС, то потенциал искомой точки будет равен потенциалу предыдущей плюс величина этой ЭДС, если направление обхода совпадает с направлением ЭДС, и минус величина ЭДС, если не совпадает. Это вытекает из того, что напряжение на источнике ЭДС имеет направление, противоположное ЭДС. Обозначив на схеме по рис. 1 точки между элементами цепи e и a и приняв потенциал точки а за нуль(
или
Таким образом, в результате проведенных вычислений получено, что В заключение заметим, что векторы напряжений ориентированы относительно точек топографической диаграммы противоположно положительным направлениям напряжений относительно соответствующих точек электрической цепи. В этой связи допускается не указывать на топографической диаграмме направления векторов напряжений. Потенциальная диаграмма Потенциальная диаграмма применяется при анализе цепей постоянного тока. Она представляет собой график распределения потенциала вдоль участка цепи или контура, при этом по оси абсцисс откладываются сопротивления резистивных элементов, встречающихся на пути обхода ветви или контура, а по оси ординат – потенциалы соответствующих точек. Таким образом, каждой точке рассматриваемого участка или контура соответствует точка на потенциальной диаграмме. Рассмотрим построение потенциальной диаграммы на примере схемы на рис. 3.
При параметрах схемы Построим потенциальную диаграмму для контура abcda. Для выбора масштаба по оси абсцисс просуммируем сопротивления резисторов вдоль рассматриваемого контура:
Таким образом, координаты точек потенциальной диаграммы: а(0;0);b(4;-20); c(4;17); d(7;2). С учетом выбранных масштабов на рис. 4 построена потенциальная диаграмма для выбранного контура. Преобразование линейных электрических схем Для упрощения расчета и повышения наглядности анализа сложных электрических цепей во многих случаях рационально подвергнуть их предварительному преобразованию. Очевидно, что преобразование должно приводить к упрощению исходной схемы за счет уменьшения числа ее ветвей и (или) узлов. Такое преобразование называется целесообразным. При этом при любых способах преобразований должно выполняться условие неизменности токов в ветвях участков схемы, не затронутых этими преобразованиями. Из последнего вытекает, что, если преобразованию подвергаются участки цепи, не содержащие источников энергии, то мощности в исходной и эквивалентной схемах одинаковы. Если в преобразуемые участки входят источники энергии, то в общем случае мощности в исходной и преобразованной цепях будут различны. Рассмотрим наиболее важные случаи преобразования электрических цепей. 1, Преобразование последовательно соединенных элементов Рассмотрим участок цепи на рис. 5,а. При расчете внешней по отношению к этому участку цепи данную ветвь можно свести к виду на рис. 5,б, где
или
2 Преобразование параллельно соединенных ветвей Пусть имеем схему на рис. 6,а.
Согласно закону Ома для участка цепи с источником ЭДС
где Тогда
причем со знаком “+” в (4) записываются ЭДС 3. Взаимные преобразования “треугольник-звезда”
Преобразовать треугольник в звезду – значит заменить три сопротивления, соединенных в треугольник между какими-то тремя узлами, другими тремя сопротивлениями, соединенными в звезду между теми же точками. При этом на участках схемы, не затронутых этими преобразованиями, токи должны остаться неизменными. Без вывода запишем формулы эквивалентных преобразований
Литература
Контрольные вопросы и задачи
Ответ:
Ответ:
Ответ: | ||||||||||||||||||||||||
| Лекция N 10. Анализ цепей с индуктивно связанными элементами. |
Электрические цепи могут содержать элементы, индуктивно связанные друг с другом. Такие элементы могут связывать цепи, электрически (гальванически) разделенные друг от друга. В том случае, когда изменение тока в одном из элементов цепи приводит к появлению ЭДС в другом элементе цепи, говорят, что эти два элемента индуктивно связаны, а возникающую ЭДС называют ЭДС взаимной индукции. Степень индуктивной связи элементов характеризуется коэффициентом связи
где М – взаимная индуктивность элементов цепи (размерность – Гн);
Пусть имеем две соосные катушки в общем случае с ферромагнитным сердечником (см. рис. 1). На рис. 1 схематично показана картина магнитного поля при наличии тока i1 в первой катушке (направление силовых линий магнитного потока определяется по правилу правого буравчика). Витки первой катушки сцеплены с магнитным потоком самоиндукцииФ11 , а витки второй катушки – с магнитным потоком взаимной индукцииФ21, который отличается от Ф11 (Ф21< Ф11) за счет потоков рассеяния. По определению
Если теперь наоборот пропустить ток i2 по второй катушке, то соответственно получим Наши рекомендации
|

 ;
;  .
.  и
и  возможны три различных случая.
возможны три различных случая. , а следовательно,
, а следовательно, . Этому режиму соответствует векторная диаграмма на рис. 2,а.
. Этому режиму соответствует векторная диаграмма на рис. 2,а.
 , а значит,
, а значит,  . Этот случай отражает векторная диаграмма на рис. 2,б.
. Этот случай отражает векторная диаграмма на рис. 2,б. - случай резонанса напряжений (рис. 2,в).
- случай резонанса напряжений (рис. 2,в). .
.  .
.

 . Тогда
. Тогда  , и, соответственно,
, и, соответственно,  .
.
 , и соотношение (3) выполняется для эквивалентных значений LЭ и CЭ .
, и соотношение (3) выполняется для эквивалентных значений LЭ и CЭ . .
.  и
и  для цепи на рис. 1 при U=const.
для цепи на рис. 1 при U=const. ,
,  .
. ,
,  можно записать:
можно записать: .
. 
 Для цепи рис. 4 имеем
Для цепи рис. 4 имеем ,
, ;
;  .
.  и
и  , как и в рассмотренном выше случае последовательного соединения элементов, возможны три различных случая.
, как и в рассмотренном выше случае последовательного соединения элементов, возможны три различных случая.
 , а следовательно,
, а следовательно,  . Этому режиму соответствует векторная диаграмма на рис. 5,а.
. Этому режиму соответствует векторная диаграмма на рис. 5,а. , а значит,
, а значит,  . Этот случай иллюстрирует векторная диаграмма на рис. 5,б.
. Этот случай иллюстрирует векторная диаграмма на рис. 5,б. - случай резонанса токов (рис. 5,в).
- случай резонанса токов (рис. 5,в). или
или .
.  . Таким образом, при резонансе токов входная проводимость цепи минимальна, а входное сопротивление, наоборот, максимально. В частности при отсутствии в цепи на рис. 4 резистора R ее входное сопротивление в режиме резонанса стремится к бесконечности, т.е. при резонансе токов ток на входе цепи минимален.
. Таким образом, при резонансе токов входная проводимость цепи минимальна, а входное сопротивление, наоборот, максимально. В частности при отсутствии в цепи на рис. 4 резистора R ее входное сопротивление в режиме резонанса стремится к бесконечности, т.е. при резонансе токов ток на входе цепи минимален. Например, для цепи на рис. 6 имеем
Например, для цепи на рис. 6 имеем
 должна быть равна нулю, то условие резонанса имеет вид
должна быть равна нулю, то условие резонанса имеет вид ,
, или входной проводимости
или входной проводимости  , определяет наличие у соответствующих этому условию уравнений относительно
, определяет наличие у соответствующих этому условию уравнений относительно  нескольких вещественных корней, т.е. таким цепям соответствует несколько резонансных частот.
нескольких вещественных корней, т.е. таким цепям соответствует несколько резонансных частот. или входной реактивной проводимости
или входной реактивной проводимости  следует представить в виде отношения двух полиномов по степеням
следует представить в виде отношения двух полиномов по степеням  или
или  . Тогда корни уравнения
. Тогда корни уравнения  дадут значения частот, которые соответствуют резонансам напряжений, а корни уравнения
дадут значения частот, которые соответствуют резонансам напряжений, а корни уравнения  - значения частот, при которых возникают резонансы токов. Общее число резонансных частот в цепи на единицу меньше количества индуктивных и емкостных элементов в схеме, получаемой из исходной путем ее сведения к цепи (с помощью эквивалентных преобразований) с минимальным числом этих элементов. Характерным при этом является тот факт, что режимы резонансов напряжений и токов чередуются.
- значения частот, при которых возникают резонансы токов. Общее число резонансных частот в цепи на единицу меньше количества индуктивных и емкостных элементов в схеме, получаемой из исходной путем ее сведения к цепи (с помощью эквивалентных преобразований) с минимальным числом этих элементов. Характерным при этом является тот факт, что режимы резонансов напряжений и токов чередуются.
 Из решения уравнения
Из решения уравнения  , соответствующую резонансу напряжений, а из решения уравнения
, соответствующую резонансу напряжений, а из решения уравнения  , соответствующую резонансу токов.
, соответствующую резонансу токов. .
. ?
?  .
. Параметры схемы:
Параметры схемы: 



 найденные значения токов (см. лекцию № 5) равны:
найденные значения токов (см. лекцию № 5) равны:  ;
;  ;
;  .
.
 ), определим потенциалы этих точек:
), определим потенциалы этих точек:


 . Но разность потенциалов точек е и а равно напряжению U, приложенному к цепи, а оно равно 120 В. Таким образом, второй закон Кирхгофа выполняется, а следовательно, вычисления выполнены верно. В соответствии с полученными результатами строится топографическая диаграмма на рис. 2. Следует обратить внимание на ориентацию векторов, составляющих топографическую диаграмму, относительно векторов тока: для резистивных элементов соответствующие векторы параллельны, для индуктивного и емкостных – ортогональны.
. Но разность потенциалов точек е и а равно напряжению U, приложенному к цепи, а оно равно 120 В. Таким образом, второй закон Кирхгофа выполняется, а следовательно, вычисления выполнены верно. В соответствии с полученными результатами строится топографическая диаграмма на рис. 2. Следует обратить внимание на ориентацию векторов, составляющих топографическую диаграмму, относительно векторов тока: для резистивных элементов соответствующие векторы параллельны, для индуктивного и емкостных – ортогональны.

 ;
;  ;
;  ;
;  ;
;  и
и  токи в ветвях схемы равны:
токи в ветвях схемы равны:  ;
;  ;
;  .
.
 после чего определим потенциалы точек контура относительно потенциала произвольно выбранной точки a, потенциал которой принят за нуль:
после чего определим потенциалы точек контура относительно потенциала произвольно выбранной точки a, потенциал которой принят за нуль:

 .
. 
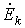 k-я ЭДС берется со знаком “+”, если ее направление совпадает с направлением эквивалентной ЭДС, и “-”, если не совпадает.
k-я ЭДС берется со знаком “+”, если ее направление совпадает с направлением эквивалентной ЭДС, и “-”, если не совпадает.
 ,
, .
. ,
, ;
;  ,
,  , если они направлены к тому же узлу, что и ЭДС
, если они направлены к тому же узлу, что и ЭДС 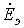 ; в противном случае они записываются со знаком “-”.
; в противном случае они записываются со знаком “-”. В ряде случаев могут встретиться схемы, соединения в которых нельзя отнести ни к последовательному, ни к параллельному типу (см. рис. 7). В таких случаях преобразования носят более сложный характер: преобразование треугольника в звезду и наоборот.
В ряде случаев могут встретиться схемы, соединения в которых нельзя отнести ни к последовательному, ни к параллельному типу (см. рис. 7). В таких случаях преобразования носят более сложный характер: преобразование треугольника в звезду и наоборот.


 и параметры всех ее элементов, качественно построить векторную диаграмму токов и топографическую диаграмму потенциалов для нее.
и параметры всех ее элементов, качественно построить векторную диаграмму токов и топографическую диаграмму потенциалов для нее. 
 .
.  .
. ;
;  ;
;  .
. ,
,  и
и  .
.  ;
;  ;
;  .
. ,
,  и
и  -собственные индуктивности этих элементов.
-собственные индуктивности этих элементов. Слеует отметить, что всегда к<1.
Слеует отметить, что всегда к<1. ;
;  .
.