Синусоидально изменяющийся ток

Из всех возможных форм периодических токов наибольшее распространение получил синусоидальный ток. По сравнению с другими видами тока синусоидальный ток имеет то преимущество, что позволяет в общем случае наиболее экономично осуществлять производство, передачу, распределение и использование электрической энергии. Только при использовании синусоидального тока удается сохранить неизменными формы кривых напряжений и токов на всех участках сложной линейной цепи. Теория синусоидального тока является ключом к пониманию теории других цепей.

Изображение синусоидальных ЭДС, напряжений
и токов на плоскости декартовых координат

Синусоидальные токи и напряжения можно изобразить графически, записать при помощи уравнений с тригонометрическими функциями, представить в виде векторов на декартовой плоскости или комплексными числами.

Приведенным на рис. 1, 2 графикам двух синусоидальных ЭДС е₁ и е₂ соответствуют уравнения:

.

Значения аргументов синусоидальных функций и называются фазамисинусоид, а значение фазы в начальный момент времени (t=0): и - начальной фазой( ).

Величину , характеризующую скорость изменения фазового угла, называют угловой частотой.Так как фазовый угол синусоиды за время одного периода Т изменяется на 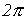рад., то угловая частота есть , где f– частота.

При совместном рассмотрении двух синусоидальных величин одной частоты разность их фазовых углов, равную разности начальных фаз, называют углом сдвига фаз.

Для синусоидальных ЭДС е₁ и е₂ угол сдвига фаз:

.

Векторное изображение синусоидально
изменяющихся величин

На декартовой плоскости из начала координат проводят векторы, равные по модулю амплитудным значениям синусоидальных величин, и вращают эти векторы против часовой стрелки (в ТОЭ данное направление принято за положительное) с угловой частотой, равной w. Фазовый угол при вращении отсчитывается от положительной полуоси абсцисс. Проекции вращающихся векторов на ось ординат равны мгновенным значениям ЭДС е₁ и е₂ (рис. 3). Совокупность векторов, изображающих синусоидально изменяющиеся ЭДС, напряжения и токи, называют векторными диаграммами.При построении векторных диаграмм векторы удобно располагать для начального момента времени (t=0), что вытекает из равенства угловых частот синусоидальных величин и эквивалентно тому, что система декартовых координат сама вращается против часовой стрелки со скоростью w. Таким образом, в этой системе координат векторы неподвижны (рис. 4). Векторные диаграммы нашли широкое применение при анализе цепей синусоидального тока. Их применение делает расчет цепи более наглядным и простым. Это упрощение заключается в том, что сложение и вычитание мгновенных значений величин можно заменить сложением и вычитанием соответствующих векторов.

Пусть, например, в точке разветвления цепи (рис. 5) общий ток 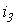равен сумме токов 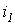и двух ветвей:

.

Каждый из этих токов синусоидален и может быть представлен уравнением

и .

Результирующий ток также будет синусоидален:

.

Определение амплитуды и начальной фазы этого тока путем соответствующих тригонометрических преобразований получается довольно громоздким и мало наглядным, особенно, если суммируется большое число синусоидальных величин. Значительно проще это осуществляется с помощью векторной диаграммы. На рис. 6 изображены начальные положения векторов токов, проекции которых на ось ординат дают мгновенные значения токов для t=0. При вращении этих векторов с одинаковой угловой скоростью w их взаимное расположение не меняется, и угол сдвига фаз между ними остается равным .

Так как алгебраическая сумма проекций векторов на ось ординат равна мгновенному значению общего тока, вектор общего тока равен геометрической сумме векторов токов:

.

Построение векторной диаграммы в масштабе позволяет определить значения и из диаграммы, после чего может быть записано решение для мгновенного значения 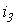путем формального учета угловой частоты: .

Представление синусоидальных ЭДС, напряжений
и токов комплексными числами

Геометрические операции с векторами можно заменить алгебраическими операциями с комплексными числами, что существенно повышает точность получаемых результатов.

Каждому вектору на комплексной плоскости соответствует определенное комплексное число, которое может быть записано в :

показательной

тригонометрической или

алгебраической - формах.

Например, ЭДС , изображенной на рис. 7 вращающимся вектором, соответствует комплексное число

.

Фазовый угол определяется по проекциям вектора на оси “+1” и “+j” системы координат, как

.

В соответствии с тригонометрической формой записи мнимая составляющая комплексного числа определяет мгновенное значение синусоидально изменяющейся ЭДС:

,

(4)

Комплексное число удобно представить в виде произведения двух комплексных чисел:

,

(5)

Параметр , соответствующий положению вектора для t=0 (или на вращающейся со скоростью w комплексной плоскости), называют комплексной амплитудой: , а параметр - комплексом мгновенного значения.

Параметр является оператором поворота вектора на угол wt относительно начального положения вектора.

Вообще говоря, умножение вектора на оператор поворота есть его поворот относительно первоначального положения на угол ±a.

Следовательно, мгновенное значение синусоидальной величины равно мнимой части без знака “j” произведения комплекса амплитуды и оператора поворота :

.

Переход от одной формы записи синусоидальной величины к другой осуществляется с помощью формулы Эйлера:

,

(6)

Если, например, комплексная амплитуда напряжения задана в виде комплексного числа в алгебраической форме:

,

- то для записи ее в показательной форме, необходимо найти начальную фазу , т.е. угол, который образует вектор с положительной полуосью +1:

.

Тогда мгновенное значение напряжения:

,

где .

При записи выражения для определенности было принято, что , т.е. что изображающий вектор находится в первом или четвертом квадрантах. Если , то при (второй квадрант)

,

(7)

а при (третий квадрант)

(8)

или

(9)

Если задано мгновенное значение тока в виде , то комплексную амплитуду записывают сначала в показательной форме, а затем (при необходимости) по формуле Эйлера переходят к алгебраической форме:

.

Следует указать, что при сложении и вычитании комплексов следует пользоваться алгебраической формой их записи, а при умножении и делении удобна показательная форма.

Итак, применение комплексных чисел позволяет перейти от геометрических операций над векторами к алгебраическим над комплексами. Так при определении комплексной амплитуды результирующего тока 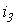по рис. 5 получим:

_где ;

.