Характеристические функции и моменты
До сих пор мы задавали случайные величины законом распределения. Характеристическая функция – ещё один способ представления случайных величин.
Пусть X – случайная величина. Её характеристической функцией f(t) назовём математическое ожидание случайной величины eitX:
f(t)=MeitX,
где под комплекснозначной случайной величиной eitXмы понимаем комплексное число eitX=costX+isintX, а
M(eitX)=M(costX)+iM(sintX);
независимая переменная t имеет размерность X-1.
Характеристическая функция – преобразование Фурье-Стилтьеса функции распределения:
f(t)= 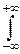 eitxdF(x).
eitxdF(x).
В непрерывном случае f(t) – преобразование Фурье плотности вероятности:
f(t)= 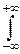 eitxp(x)dx.
eitxp(x)dx.
Если f(t) абсолютно интегрируема, то обратное преобразование Фурье позволяет восстановить плотность p(x) по характеристической функции:
p(x)= 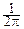
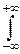 e-itxf(t)dt.
e-itxf(t)dt.
В дискретном случае:
f(t)= 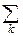 eitxkpk.
eitxkpk.
Особо отметим дискретные случайные величины с целочисленными значениями, например, при xk=k:
f(t)= 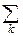 eitkpk;
eitkpk;
здесь f(t) – ряд Фурье в комплексной форме, вероятности pkиграют роль коэффициентов Фурье и легко восстанавливаются по f(t):
pk= 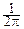
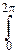 e-iktf(t)dt.
e-iktf(t)dt.
В общем случае восстановление закона распределения по характеристической функции тоже возможно, но более сложно.
Важнейшим свойством характеристической функции, сделавшим её одним из главных инструментов современной теории вероятностей, оказалось то, что при суммировании независимых случайных величин их характеристические функции перемножаются: если X и Y независимы, то для случайной величины Z=X+Y: fZ(t)=fX(t)×fY(t).
Действительно,
fZ(t)=M(eitZ)=M(eit(X+Y))=M(eitX×eitY)=M(eitX)×M(eitY)=fX(t)×fY(t).
Законы распределения при суммировании независимых слагаемых ведут себя гораздо сложнее. Например, в непрерывном случае по свойству преобразования Фурье произведению характеристических функций соответствует свёртка плотностей:
pZ(z)= 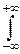 pX(x)×pY(z-x)dx.
pX(x)×pY(z-x)dx.
Если Y=aX+b, то
fY(t)=M(eit(aX+b))=eitb×M(eitaX)=eitb×fX(at).
Другим важным свойством характеристических функций является их простая связь с моментами.
Начальным моментом порядка k называется mk=M(Xk).
Центральным моментом порядка k называется mk=M[(X-MX)k].
В частности, MX=m1, DX=m2. Отметим также, что m0=1, m0=1, m1=0.
Предполагая возможность дифференцирования под знаком математического ожидания в равенстве f(t)=MeitX, получим: f(k)(t)=ikM(Xk×eitX).
При t=0: f(k)(0)=ikM(Xk)=ikmk Û mk= 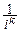 f(k)(0).
f(k)(0).
Таким образом, характеристическая функция позволяет заменить интегрирование при вычислении моментов дифференцированием.
В частности,
MX=m1= 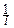 f¢(0), DX=m2-m12=-f¢¢(0)+[f¢(0)2].
f¢(0), DX=m2-m12=-f¢¢(0)+[f¢(0)2].
Если характеристическая функция f(t) разлагается в ряд Маклорена, то
f(t)= 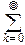
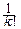 f(k)(0)tk=
f(k)(0)tk= 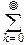
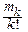 (it)k,
(it)k,
и, если моменты существуют, то они однозначно определяют f(t), т. е. закон распределения случайной величины X. Таким образом, совокупность начальных моментов также может задавать случайную величину.
Центральные моменты просто связаны с начальными:
mk=M[(X-MX)k]= 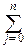 (-1)k-j
(-1)k-j 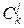 mjm1k-j, k=2, 3, ¼ .
mjm1k-j, k=2, 3, ¼ .
Обратно: начальные моменты mkможно вычислять, зная центральные мо-
менты mkи математическое ожидание m1:
mk=M{[(X-MX)+MX]k}= 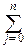
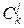 mjm1k-j, k=2, 3, ¼ .
mjm1k-j, k=2, 3, ¼ .
Характеристическую функцию определяют также и для n-мерной случайной величины (X1, X2, , ¼ , Xn):
f(t1, t2, , ¼ , tn)=M(expi(t1X1+t2X2+¼+tnXn)).
Например, для n-мерного нормального закона:
f(t1, ¼ , tn)= 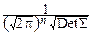
 exp[i(t1X1+¼+tnXn)-
exp[i(t1X1+¼+tnXn)- 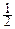 (x-a)TD-1(x-a)]dx1¼dxn=
(x-a)TD-1(x-a)]dx1¼dxn=
=exp(iaTt- 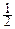 tTDt),
tTDt),
где a и t задаются как столбцы, в чём можно убедиться, осуществляя преобразования, описанные в теореме 18°.
Вычисление f(t), MX и DX для основных распределений
1°. X~B(n, p).
f(t)= 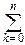 eikt
eikt 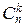 pkqn-k=(peit+q)n.
pkqn-k=(peit+q)n.
Небольшое упражнение на дифференцирование даёт:
MX= 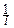 f¢(0)=np, DX=-f¢¢(0)+[f¢(0)2]=npq.
f¢(0)=np, DX=-f¢¢(0)+[f¢(0)2]=npq.
2°. X~P(l).
f(t)= 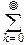 eikt
eikt 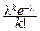 =e-l
=e-l 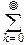
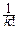 (leit)k=exp[l(eit-1)].
(leit)k=exp[l(eit-1)].
Отсюда сразу найдём: MX=l, DX=l.
3°. X~R(a, b).
f(t)= 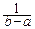
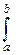 eitxdx=
eitxdx= 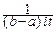 (eitb-eita).
(eitb-eita).
Отсюда находим: MX= 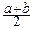 , DX=
, DX= 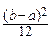 .
.
4°. X~Exp(m).
f(t)=m 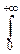 eitx-mxdx=
eitx-mxdx= 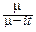 .
.
Из этого равенства: MX= 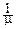 , DX=
, DX= 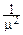 .
.
5°. X~N(0, 1).
f(t)= 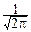
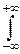
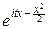 dx.
dx.
Примем во внимание, что eitx=costx+isintx:
f(t)= 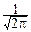
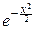 costxdx+
costxdx+ 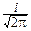
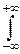
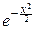 sintxdx.
sintxdx.
Второй из этих интегралов равен нулю, так как его подынтегральная функция нечётна. Ввиду чётности подынтегральной функции первого интеграла:
f(t)= 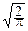
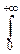
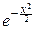 costxdx.
costxdx.
Обозначим: J(t)= 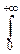
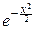 costxdx.
costxdx.
Очевидно,
J¢(t)=- 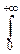 x
x 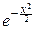 sintxdx=
sintxdx= 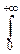 sintx
sintx 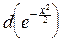 ;
;
интегрируем по частям:
J¢(t)=sintx× 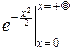 -t
-t 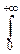
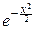 costxdx=-tJ(t).
costxdx=-tJ(t).
Таким образом, J¢(t)=-tJ(t), причём J(0)= 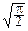 .
.
Решение этого дифференциального уравнения находится без труда:
J(t)= 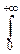
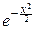 costxdx=
costxdx= 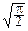
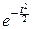 .
.
Окончательно: f(t)= 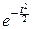 .
.
Отсюда для X~N(a, s): f(t)= 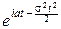 и сразу же находим: MX=a, DX=s2.
и сразу же находим: MX=a, DX=s2.
По поводу характеристической функции нормального закона можно заметить интересное его свойство:
сумма независимых нормально распределённых случайных величин распределена по нормальному закону.
Действительно. Пусть X и Y независимые случайные величины, причём, X~N(a1, s1), Y~N(a2, s2), а Z=X+Y.
Характеристические функции X и Y: fX(t)= 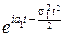 , fY(t)=
, fY(t)= 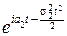 .
.
Для характеристической функции Z имеем:
fZ(t)=fX(t)×fY(t)=exp[i(a1+a2)t- 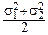 t2],
t2],
но это означает, что Z~N(a1+a2, 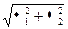 ).
).
Аналогичным свойством обладают и независимые пуассоновские случайные величины:
сумма независимых случайных величин, распределённых по закону Пуассона, распределена по закону Пуассона.
В самом деле, если X~P(l1), X~P(l2), то
fX(t)=exp[l1(eit-1)], fY(t)=exp[l2(eit-1)],
поэтому характеристическая функция случайной величины Z=X+Y:
fZ(t)=fX(t)×fY(t)=exp[(l1+l2)(eit-1)],
но это значит, что Z~P(l1+l2).
Законы, сохраняющиеся при сложении независимых случайных величин, называются безгранично делимыми. Нормальный и пуассоновский – примеры таких законов.
|
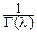 mlxl-1e-mx, если x>0,
mlxl-1e-mx, если x>0,
0, если x£0.
Найдём характеристическую функцию гамма-распределения. Имеем:
f(t)= 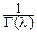 ml
ml 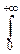 xl-1e-x(m-it)dx.
xl-1e-x(m-it)dx.
Положим в интеграле x= 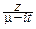 :
:
f(t)= 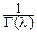
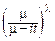
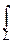 zl-1e-zdz,
zl-1e-zdz,
где интегрирование проводится по бесконечному лучу L, выходящему из начала координат и проходящему через точку m-it. Можно доказать, что этот интеграл равен G(l). Поэтому: f(t)= 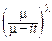 .
.
Сравнивая характеристические функции гамма-распределения и экспоненциального распределения, можно сделать следующий вывод:
сумма k независимых экспоненциальных слагаемых Xi~Exp(m) распределена по закону G(k, m).
––²––
Иногда в сокращённых курсах теории вероятностей тему "характеристические функции" исключают. Принимая это во внимание, дадим независимый от этой темы вывод значений MX и DX основных распределений.
1°. X~B(n, p).
|
1, если в i-ой попытке произошёл "успех",
0, если в i -ой попытке произошла "неудача".
Очевидно,
MXi=p, M(Xi2)=12×p+02×q=p, DXi=pq.
Кроме того, X= 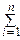 Xi, причём слагаемые здесь независимы. Поэтому:
Xi, причём слагаемые здесь независимы. Поэтому:
MX= 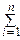 MXi=np, DX=
MXi=np, DX= 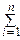 DXi=npq,
DXi=npq,
2°. X~P(l).
Продифференцируем по l тождество 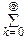
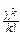 e-l=1:
e-l=1: 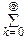 k
k 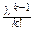 e-l-
e-l- 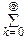
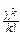 e-l=0, откуда:
e-l=0, откуда:
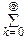 k
k 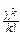 e-l=l. (*)
e-l=l. (*)
Продифференцируем (*) по l ещё раз: 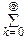 k2
k2 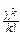 e-l-
e-l- 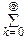 k
k 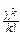 e-l=1, или:
e-l=1, или:
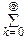 k2
k2 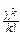 e-l=l2+l. (**)
e-l=l2+l. (**)
Из (*): MX=l; из (*) и (**): DX=M(X2)-M(X)2=(l2+l)-l2=l.
3°. X~R(a, b).
MX= 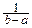
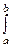 xdx=
xdx= 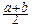 ; DX=
; DX= 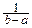
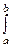 (x-
(x- 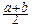 )2dx=
)2dx= 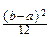 .
.
4°. X~Exp(m).
Рассмотрим интеграл: I= 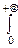 e-mxdx=
e-mxdx= 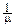 . Дважды продифференцируем его по параметру m:
. Дважды продифференцируем его по параметру m: 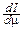 =-
=- 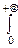 xe-mxdx=-
xe-mxdx=- 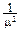 ,
, 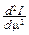 =
= 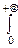 x2e-mxdx=
x2e-mxdx= 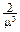 .
.
Поэтому:
MX=m 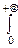 xe-mxdx=-
xe-mxdx=- 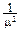 , M(X2)=m
, M(X2)=m 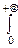 x2e-mxdx=
x2e-mxdx= 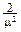 , DX=M(X2)-M(X)2=
, DX=M(X2)-M(X)2= 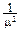 .
.
5°. X~N(a, s).
Найдём математическое ожидание X:
MX= 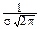
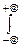 x
x 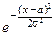 dx.
dx.
Положим в интеграле 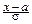 =y и представим его как сумму двух интегралов:
=y и представим его как сумму двух интегралов:
MX= 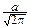
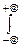
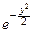 dy+
dy+ 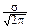
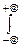 y
y 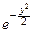 dy Û MX=a.
dy Û MX=a.
Вычислим дисперсию:
DX= 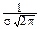
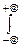 (x-a)2
(x-a)2 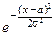 dx.
dx.
Замена переменной 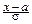 =y приводит интеграл к виду
=y приводит интеграл к виду
DX= 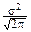
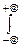 y2
y2 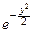 dy=x
dy=x 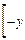
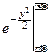 +
+ 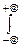
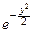 dy
dy 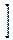 Û DX=s2.
Û DX=s2.
Предельные теоремы
1°. Локальная теорема Муавра-Лапласа.
Теорема Муавра-Лапласа устанавливает условия, при которых биномиальную случайную величину можно приближённо рассматривать как нормальную.
Пусть X~B(n, p). При n®¥ и любых фиксированных a и b, a£b:
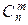 pmqn-m~
pmqn-m~ 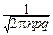 exp[-
exp[- 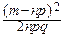 ] *)
] *)
для любых m, удовлетворяющих неравенствам: a£ 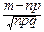 £b.
£b.
Доказательство. ƒ Доказательство теоремы основывается на формуле Стирлинга: при n®¥: n!~ 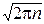 nne-n.
nne-n.
Введём величину y= 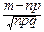 Û m=np+y
Û m=np+y 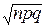 Û n-m=nq-y
Û n-m=nq-y 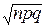 .
.
Величина y по условию оказывается ограниченной. Пусть n®¥, а m рассматриваем лишь такие, при которых a£y£b. Тогда:
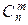 pmqn-m=
pmqn-m= 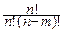 pmqn-m~
pmqn-m~ 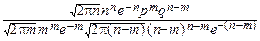 =
=
= 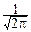
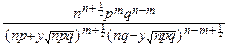 =
= 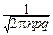 (1+y
(1+y 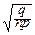 )-m-
)-m- 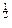 (1-y
(1-y 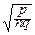 )-n+m-
)-n+m- 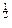 =
=
= 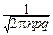 exp[-(m+
exp[-(m+ 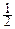 )ln(1+y
)ln(1+y 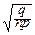 )-(n-m+
)-(n-m+ 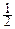 )ln(1-y
)ln(1-y 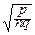 )]=
)]=
= 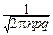 exp[-(np+y
exp[-(np+y 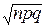 +
+ 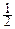 )(y
)(y 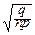 -
- 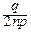 y2+¼)-
y2+¼)-
-(nq-y 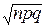 +
+ 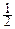 )(-y
)(-y 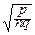 -
- 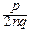 y2+¼)]~
y2+¼)]~
отбрасываем в показателе экспоненты бесконечно малые величины выше второго порядка:
~ 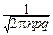 exp(-y
exp(-y 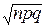 +
+ 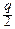 y2-qy2+y
y2-qy2+y 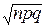 +
+ 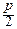 y2-py2)=
y2-py2)= 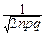
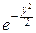 ,
,
что и требовалось доказать. ‚
Таким образом, при больших n, умерено больших m и фиксированном p (0<p<1) можно приближённо заменять биномиальное распределение нормальным: B(n, p)»N(np, 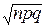 ).
).
Ошибка приближения зависит от того, достаточно ли велико n, не слишком ли близко p к 0 или к 1 и каково интересующее нас значение m. Эта ошибка в настоящее время хорошо изучена и оценена; при необходимости всю нужную информацию можно найти в литературе.
2°. Интегральная теорема Муавра-Лапласа.
Пусть X~B(n, p). Тогда при n®¥ и любых фиксированных a и b, a£b:
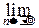 P{a£
P{a£ 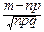 £b}=
£b}= 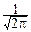
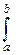
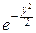 dy.
dy.
Доказательство. á Обозначим: ym= 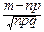 . Имеем:
. Имеем:
P{a£ 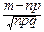 £b}=
£b}= 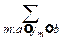
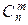 pmqn-m~
pmqn-m~
но для всех m, по которым нужно суммировать, выполнена локальная теорема Муавра-Лапласа, так что:
~ 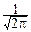
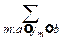
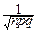
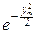 =
=
соседние точки суммирования ymнаходятся друг от друга на расстоянии Dym=
=ym+1-ym= 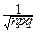 . Поэтому, в соответствии с определением определённого интеграла:
. Поэтому, в соответствии с определением определённого интеграла:
= 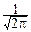
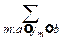
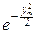 Dym
Dym 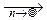
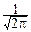
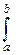
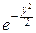 dy. à
dy. à
Теорема Муавра-Лапласа позволяет уточнить связь относительной частоты и вероятности. Поскольку абсолютная частота m события A, имеющего вероятность p, распределена по биномиальному закону B(n, p), то
P{| 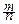 -p|£e}=P{-e£
-p|£e}=P{-e£ 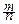 -p£e}=P{-e
-p£e}=P{-e 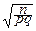 £
£ 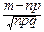 £e
£e 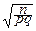 }»
}»
» 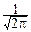
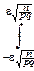
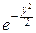 dy=F(e
dy=F(e 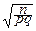 ).
).
По этой формуле можно приближённо находить вероятность a заданного отклонения относительной частоты от вероятности, вычислять необходимое число опытов n, при котором с данной вероятностью a указанное отклонение не превышает e. Исходное уравнение выглядит так: F(e 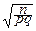 )=a.
)=a.
3°. Центральная предельная теорема.
Переформулируем интегральную теорему Муавра-Лапласа, введя вспомогательные случайные величины, связанные со схемой Бернулли:
|
0, если в i-ом испытании произошла "неудача".
Тогда Sn= 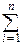 Xi=m, и MSn=
Xi=m, и MSn= 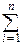 MXi=np, DSn=
MXi=np, DSn= 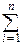 DXi=npq, и теорему Муавра-Лапласа можно сформулировать так:
DXi=npq, и теорему Муавра-Лапласа можно сформулировать так:
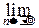 P{a£
P{a£ 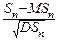 £b}=
£b}= 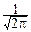
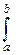
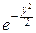 dy,
dy,
т. е. центрированная и нормированная сумма Snдостаточно большого числа случайных величин Xiприближённо распределена по стандартному нормальному закону. Оказалось, что аналогичное утверждение верно для весьма широкого класса слагаемых, и центральная предельная теорема указывает точные ограничения (оказавшиеся весьма слабыми), которые нужно наложить на слагаемые, чтобы их центрированная и нормированная сумма в пределе была распределена по стандартному нормальному закону. Грубо говоря, смысл этих ограничений состоит в том, что слагаемые случайные величины должны быть более или менее равноправны. Именно центральная предельная теорема приводит, например, к тому, что большинство физических измерений приводят к нормально распределённым результатам: на результат отдельного измерения накладываются многие мелкие факторы, и суммарная ошибка по центральной предельной теореме оказывается нормально распределенной случайной величиной.
В качестве примера изложим здесь центральную предельную теорему в наиболее простом варианте: для одинаково распределённых слагаемых, имеющих дисперсию. Пусть Xi, i=1, 2, ¼ – независимые случайные величины с одной и той же функцией распределения F(x). Характеристическая функция их равна f(t)= 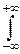 eitxdF(x).
eitxdF(x).
Очевидно, если существует k-й начальный момент mk:
mk= 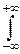 xkdF(x),
xkdF(x),
то существует и производная k-го порядка характеристической функции:
f(k)(t)=ik 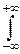 xkeitxdF(x),
xkeitxdF(x),
ибо |eitx|=1. Если существует момент второго порядка m2(т.е. дисперсия), то по формуле Тейлора, отсюда следует, что можно при t®0 представить характеристическую функцию в форме
f(t)=f(0)+ 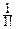 f¢(0)t+
f¢(0)t+ 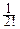 f¢¢(0)t2+o(t2)=1+m1it+
f¢¢(0)t2+o(t2)=1+m1it+ 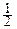 m2(it)2+o(t2).
m2(it)2+o(t2).
Рассмотрим сумму Sn= 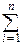 Xi. Её центрирование и нормирование даёт:
Xi. Её центрирование и нормирование даёт:
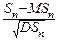 =
= 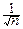
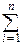
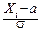 ,
,
где a=MXi, s2=Dxi. Случайная величина 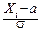 имеет моменты m1=0, m2=1. Её характеристическая функция представляется в виде: f(t)=1-
имеет моменты m1=0, m2=1. Её характеристическая функция представляется в виде: f(t)=1- 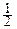 t2+o(t2), а характеристическая функция fn(t) центрированной и нормированной суммы Sn, очевидно, равна:
t2+o(t2), а характеристическая функция fn(t) центрированной и нормированной суммы Sn, очевидно, равна:
fn(t)=[1- 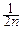 t2+o(
t2+o( 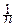 t2)]n=exp[nln(1-
t2)]n=exp[nln(1- 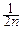 t2+o(
t2+o( 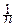 t2)]
t2)]
и при n®¥: fn(t)® 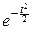 .
.
Характеристическая функция центрированной и нормированной суммы сходится к характеристической функции стандартного нормального закона. Отсюда можно вывести, что и функция распределения центрированной и нормированной суммы сходится к функции распределения нормального закона.
4°. Теорема Пуассона.
Теорема Пуассона устанавливает условия, при которых биномиальную случайную величину можно приближённо считать пуассоновской.
Докажем сначала чисто аналитический факт:
При любом фиксированном l>0, любом фиксированном целом m³0 и при n®¥: 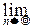
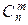
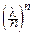
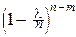 =
= 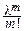 e-l.
e-l.
á Действительно,
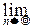
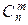
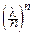
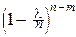 =
= 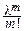
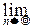 [
[ 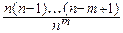
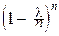
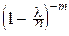 ]=
]=
= 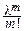
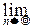 [
[ 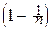
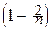 ¼
¼ 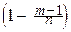 ]
] 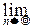
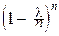
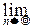
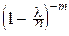 =
= 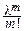 e-l. à
e-l. à
Для достаточно больших n величина 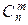
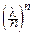
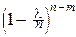 становится как угодно близкой к своему пределу. Обозначая
становится как угодно близкой к своему пределу. Обозначая 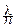 =p, Û l=np, можем записать приближённое равенство:
=p, Û l=np, можем записать приближённое равенство:
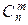 pmqn-m»
pmqn-m» 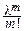 e-l,
e-l,
т. е. биномиальные вероятности можно считать пуассоновскими: B(n, p)»
»P(l), причём l=np. Поскольку в точной формулировке m и l фиксированы, а n®¥, то можно рассчитывать на малую погрешность приближения при большом n, малом p и умеренном np.
*) Знак "~" означает, что левая и правая части являются эквивалентными величинами, т. е. предел их отношения равен 1. При конечном и достаточно большом n этот знак можно понимать как знак приближённого равенства.