Двумерные случайные веЛИчины
Двумерной случайной величиной называется пара случайных величин, определённых на вероятностном пространстве (W, Å, P(×)). Результат наблюдения двумерной случайной величины (X, Y) можно изобразить точкой (x, y) на плоскости. Закон распределения вероятностей между возможными значениями двумерной случайной величины даётся совместной функцией распределения:
F(x, y)=P{X<x, Y<y}
|

|
Запятая в записи вероятности P{X<x, Y<y} заменяет знак умножения между событиями {X<x} и {Y<y}.
Выделим два простейших случая: непрерывный и дискретный.
Двумерная случайная величина (X, Y) называется непрерывной, если существует такая функция p(x, y), что
F(x, y)= 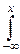
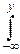 p(x, y)dxdy.
p(x, y)dxdy.
Очевидно, p(x, y)= 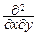 F(x, y).
F(x, y).
Функция p(x, y) называется совместной плотностью вероятности; она играет роль поверхностной плотности распределения единичной вероятностной массы на двумерной плоскости. Вероятность того, что (X, Y) попадёт в область A на двумерной плоскости, вычисляется так:
P(A)= 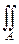 p(x, y)dxdy,
p(x, y)dxdy,
и эта вероятность определена для таких событий A, для которых определён интеграл справа.
В дискретном случае возможные значения (X, Y) можно представить как упорядоченные пары чисел (xi, yj) и закон распределения давать в виде таблицы: pij=P{X=xi, Y=yj}.
Если известен закон распределения двумерной случайной величины (X, Y), то можно найти также законы распределения компонент X и Y.
В общем случае:
FX(x)=P{X<x}=P{X<x, Y<+¥}=F(x, +¥).
Аналогично: FY(y)=F(+¥, y).
В непрерывном случае:
pX(x)= 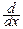 FX(x)=
FX(x)= 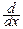 F(x, +¥)=
F(x, +¥)= 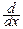
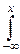 dx
dx  p(x, y)dy=
p(x, y)dy=  p(x, y)dy.
p(x, y)dy.
Аналогично:
pY(y)=  p(x, y)dx.
p(x, y)dx.
В дискретном случае:
pi=P{X=xi}=P{X=xi, -¥<Y<+¥}= 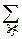 pij.
pij.
Аналогично:
qj=P{Y=yj}= 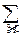 pij.
pij.
Обратная задача – восстановить закон распределения двумерной случайной величины по законам распределения компонент – решается для независимых компонент.
Естественно называть случайные величины X и Y независимыми, если события {X<x} и {Y<y} независимы, т. е., если
F(x, y)=P{X<x, Y<y}=P{X<x}P{Y<y}=FX(x)FY(y).
Если F(x, y) дифференцируема, то
p(x, y)= 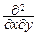 F(x, y)=
F(x, y)= 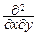 FX(x)FY(y)=
FX(x)FY(y)= 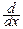 FX(x)
FX(x) 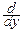 FY(y)=pX(x)pY(y).
FY(y)=pX(x)pY(y).
В дискретном случае:
pij=P{X=xi, Y=yj}=P{X=xi}P{Y=yj}=piqj.
Совершенно аналогично вводятся n-мерные случайные величины.
Например, пусть независимые случайные величины Xi, i=1, 2, ¼ , n распределены по стандартному нормальному закону: Xi~N(0, 1), i=1, 2, ¼ , n. Их совместная плотность вероятности равна:
p(x1, x2, ¼ , xn)= 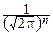 exp(-
exp(- 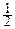
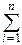 xi2).
xi2).
Выполним невырожденное линейное преобразование и введём новые случайные величины
Yk= 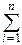 aijXi, k=1, 2, ¼ , n.
aijXi, k=1, 2, ¼ , n.
Это преобразование можно переписать в матричном виде: Y=AX, где XT=
=(X1, X2, ¼ , Xn), YT=(Y1, Y2, ¼ , Yn), A=||aij||, DetA¹0. Так как преобразование невырождено, то оно обратимо, так что X=A-1Y. В евклидовом пространстве переменных y1, y2, ¼ , ynсовместная плотность вероятности вектора Y равна
q(y1, y2, ¼ , yn)= 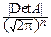 exp(-
exp(- 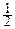 YTSY),
YTSY),
где S=ATA – матрица квадратичной формы в показателе экспоненты, а |DetA|=J – якобиан преобразования.
Обратно, если совместная плотность вероятности n-мерного вектора равна
q(y1, y2, ¼ , yn)=C×exp(- 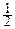 YTSY),
YTSY),
где S – положительно определённая матрица (что нужно для сходимости интеграла по всему пространству), а C – константа, то существует такая матрица A, что S=ATA, С=|DetA|= 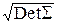 и преобразование Y=AX, (X=A-1Y) приводит к независимым компонентам Xi~N(0, 1), i=1, 2, ¼ , n.
и преобразование Y=AX, (X=A-1Y) приводит к независимым компонентам Xi~N(0, 1), i=1, 2, ¼ , n.
Можно сделать ещё одно обобщение, введя параметры масштаба и сдвига по всем осям.
n-мерной нормальной плотностью называется
p(x1, x2, ¼ , xn)= 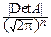 exp(-
exp(- 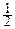
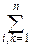 aik(xi-bi)(xk-bk)),
aik(xi-bi)(xk-bk)),
где aik, bi– параметры n-мерного нормального вектора, A=||aij|| – положительно определённая матрица.
c2– распределение
Пусть X1, X2, ¼ , Xn– независимые (в совокупности) нормально распределённые случайные величины: Xi~N(0, 1), i=1, 2, ¼ , n.
Определим сумму их квадратов:
cn2= 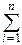 Xi2
Xi2
и найдём закон распределения случайной величины cn2:
Fcn2(x)= 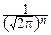
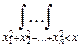 exp(-
exp(- 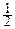
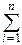 xi2)dx1dx2¼dxn, x>0.
xi2)dx1dx2¼dxn, x>0.
Принимая во внимание, что подынтегральная функция принимает постоянное значение на любой n-мерной сфере (x12+x22+¼+xn2=r2), проведём интегрирование по сферическим слоям. Обозначим через Vn(r) объём n-мерной сферы радиуса r, а через Sn(r) – площадь её поверхности.
Отметим, что:
Sn(r)= 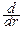 Vn(r), Vn(r)=
Vn(r), Vn(r)= 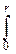 Sn(r)dx.
Sn(r)dx.
В частности, в двумерном и трёхмерном случаях имеем:
V2(r)=pr2, S2(r)=2pr, V3(r)= 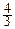 pr3, S3(r)=4pr2.
pr3, S3(r)=4pr2.
Ясно, что можно считать
Vn(r)=Cnrn, Sn(r)=nCnrn-1,
где Cn– константа, которую мы найдём ниже.
Продолжим теперь преобразование функции распределения cn2:
Fcn2(x)= 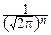
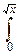 exp(-
exp(- 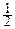 r2)nCnrn-1dr.
r2)nCnrn-1dr.
Мы превратили n-кратный интеграл в обычный однократный.
Из последнего равенства найдём плотность вероятности:
pcn2(x)= 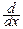 Fcn2(x)=
Fcn2(x)= 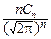 exp(-
exp(- 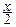 )
) 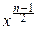
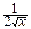 Û pcn2(x)=
Û pcn2(x)= 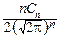
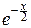
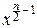 , x>0.
, x>0.
Если x£0, то ясно, что pcn2(x)º0.
Прежде, чем перейти к вычислению константы Cn, напомним определение и свойства гамма-функции, которыми нам ещё не раз придётся пользоваться.
––²––
Определение и свойства гамма-функции
Гамма-функция определена на положительной полуоси равенством:
G(x)=  e-ttx-1dt, x>0.
e-ttx-1dt, x>0.
Свойства гамма-функции:
1°. G(x+1)=xG(x). Это свойство легко доказывается интегрированием по частям интеграла, определяющего G(x+1): G(x+1)=  e-ttxdt.
e-ttxdt.
2°. G(1)=1.
3°. Для любого натурального n: G(n+1)=n! Доказательство этого факта сразу следует из двух первых свойств. Данное свойство показывает, что гамма-функция является естественным обобщением факториала.
4°. G( 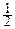 )=
)= 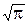 .
.
Для доказательства этого свойства достаточно сделать замену переменной в интеграле, определяющем G( 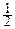 ):
):
G( 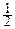 )=
)=  e-t
e-t 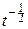 dt
dt
и положить t= 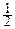 y2:
y2:
G( 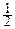 )=
)= 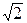

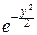 dy.
dy.
Вспоминая рассмотренный нами выше интеграл Пуассона I= 
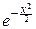 dx=
dx= 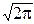 , находим, что G(
, находим, что G( 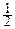 )=
)= 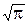 .
.
5°. Для полуцелого положительного n: G(n+ 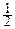 )=
)= 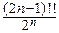
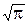 .
.
Это равенство доказывается по индукции с использованием свойств 1° и 4°.
6°. Формула Стирлинга:
при x®+¥: G(x+1)~ 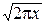 xxe-x.
xxe-x.
Мы приведём не вполне строгое, но достаточно простое доказательство этой формулы.
При любом фиксированном x (x>0):
G(x+1)=  e-ttxdt=
e-ttxdt=  exlnt-tdt=
exlnt-tdt=  ey(t)dt,
ey(t)dt,
где y(t)=xlnt-t.
Легко убедиться, что функция y(t) имеет максимум при t=x. Разложим y(t) в ряд Тейлора в окрестности точки t=x, ограничиваясь первыми тремя слагаемыми:
y(t)»xlnx-x- 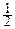
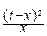 =xlnx-x-
=xlnx-x- 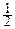 (
( 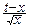 )2.
)2.
Поэтому
G(x+1)»exlnx-x 
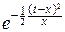 dt=xxe-x
dt=xxe-x 
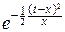 dt.
dt.
Введём новую переменную: y= 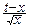 . Имеем:
. Имеем:
G(x+1)»xxe-x 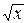
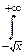
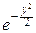 dy.
dy.
В последнем интеграле при больших x (x®+¥) нижний предел интегрирования можно заменить на -¥: 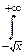
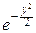 dy»
dy» 
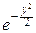 dy=I – интеграл Пуассона и, как мы знаем, он равен
dy=I – интеграл Пуассона и, как мы знаем, он равен 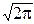 . Поэтому при больших положительных x:
. Поэтому при больших положительных x:
G(x+1)»xxe-x 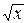
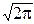 ,
,
что и требовалось доказать.
––²––
Выше мы получили выражение для плотности вероятности pcn2(x):
pcn2(x)= 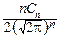
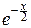
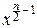 при x>0 и pcn2(x)º0 при x£0
при x>0 и pcn2(x)º0 при x£0
и нам осталось найти величину константы Cn.
Воспользуемся свойством нормированности pcn2(x):
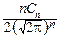

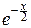
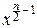 dx=1.
dx=1.
Подстановка x= 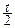 приводит интеграл к гамма-функции:
приводит интеграл к гамма-функции:
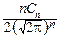
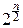 ×
×  e-t
e-t 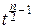 dt=1 Û
dt=1 Û 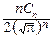 G(
G( 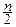 )=1 Û Cn=
)=1 Û Cn= 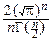 =
= 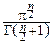 .
.
Итак, мы можем в окончательном виде записать плотность вероятности и функцию распределения случайной величины cn2:
pcn2(x)= 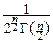
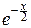
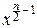 , при x>0, и pcn2(x)º0, при x£0,
, при x>0, и pcn2(x)º0, при x£0,
Fcn2(x)= 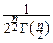
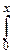
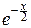
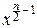 dx, при x>0, и Fcn2(x)º0, при x£0.
dx, при x>0, и Fcn2(x)º0, при x£0.
Этот закон табулирован и нет необходимости вычислять интеграл точно даже для чётных n, при которых он берётся в элементарных функциях.
Попутно мы нашли общие формулы для объёма n-мерного шара и площади поверхности n-мерной сферы:
Vn(r)= 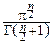 rn, Sn(r)=
rn, Sn(r)= 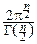 rn-1.
rn-1.
C– распределение
При y>0:
Fcn(y)=P{cn<y}=P{cn2<y2}= 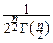
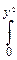
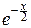
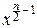 dx.
dx.
Отсюда:
pcn(y)= 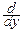 Fcn(y)=
Fcn(y)= 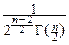
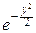 yn-1, при y>0, и pcn(y)º0, при y£0.
yn-1, при y>0, и pcn(y)º0, при y£0.
и, следовательно,
Fcn(x)= 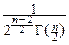
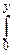
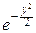 yn-1dy, при y>0 и Fcn(x)º0, при y£0.
yn-1dy, при y>0 и Fcn(x)º0, при y£0.
Распределение Стьюдента
Пусть даны две независимые случайные величины X~N(0, 1), и cn.
Определим случайную величину Tn равенством: Tn= 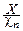 и найдём закон её распределения.
и найдём закон её распределения.
Совместная плотность вероятности двумерной случайной величины (X, cn) равна:
p(x, y)= 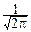
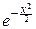
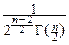
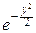 yn-1, для -¥<x<+¥, 0<y<+¥.
yn-1, для -¥<x<+¥, 0<y<+¥.
Функция распределения дроби Tn равна:
FTn(t)=P{Tn<t}=P{ 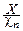 <t}=P{X<tcn}.
<t}=P{X<tcn}.
Неравенству X<tcn благоприятствуют точки, занимающие область, заштрихованную на Рис. 3:
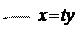
 |
Этой области досталась вероятность:
FTn(t)=P{Tn<t}=  dy
dy 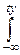 p(x, y)dx=
p(x, y)dx= 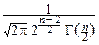
 dy
dy 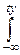
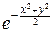 yn-1dx.
yn-1dx.
Отсюда находим плотность вероятности:
pTn(t)= 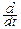 FTn(t)=
FTn(t)= 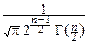
 yn-1
yn-1 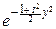 ydy.
ydy.
Отметим, что в интеграле t играет роль параметра и сделаем замену переменной:
u= 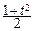 y2 Þ y=
y2 Þ y= 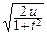 Þ dy=
Þ dy= 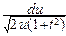 .
.
Имеем:
pTn(t)= 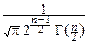 ×
× 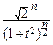 ×
× 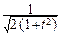
 e-u
e-u 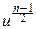 du
du
и, выражая интеграл через гамма-функцию, мы можем записать плотность распределения Стьюдента в следующем – окончательном виде:
pTn(t)= 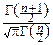 ×
× 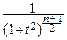 .
.
Отметим, что при n=1 из этой формулы получается плотность распределения Коши:
pT1(t)= 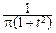 ,
,
т. е. случайную величину, распределенную по закону Коши, можно считать отношением двух независимых случайных величин, X= 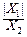 , где Xi~N(0, 1), i=1, 2.
, где Xi~N(0, 1), i=1, 2.
Замечание. Часто случайную величину Tnопределяют с дополнительным множителем: Tn= 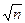 ×
× 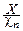 . В этом случае плотность вероятности имеет вид:
. В этом случае плотность вероятности имеет вид:
pTn(t)= 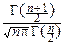 ×(1+
×(1+ 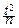 )
) 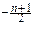 .
.
Дополнительные множители появляются и в выражении для функции распределения.
Числовые характеристики случайных величин:
математическое ожидание, дисперсия,
коэффициент корреляции
Наиболее полная информация о случайной величине содержится в законе её распределения. Более бедную, но зато и более конкретную информацию о ней дают её числовые характеристики. Простейшей из них является математическое ожидание, которое интерпретируется как среднее значение случайной величины. Если посмотреть на закон распределения как на распределение единичной вероятностной массы между значениями случайной величины, то в качестве среднего значения можно взять координаты центра тяжести этой массы. По известным из анализа и механики формулам получаем формулы для вычисления абсциссы центра тяжести:
 xp(x)dx – в непрерывном случае,
xp(x)dx – в непрерывном случае,
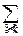 xkpk– в дискретном случае.
xkpk– в дискретном случае.
Для того, чтобы дать определение, пригодное и для общего случая, необходимо обобщить понятие риманова интеграла.
Сделаем поэтому небольшое математическое отступление.
––²––
Интеграл Стилтьеса
Интеграл Стилтьеса определяется для двух функций: одна из них j(x) – называется интегрируемой, другая F(x) – интегрирующей. Разобьём всю ось на интервалы Dtk: [tk, tk+1), относя для определённости к интервалу левый конец и исключая правый. В каждом интервале выберем произвольно точку xkи составим интегральную сумму
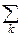 j(xk)[F(tk+1)-F(tk)].
j(xk)[F(tk+1)-F(tk)].
Перейдём к пределу, устремив наибольший из интервалов к нулю. Если предел существует и не зависит ни от способа разбиения оси на интервалы, ни от способа выбора точек xkна них, то он называется интегралом Стилтьеса от функции j(x) по функции F(x) и обозначается:  j(x)dF(x).
j(x)dF(x).
Легко убедиться в том, что обычные свойства интеграла сохраняются: постоянный множитель можно выносить за знак интеграла, интеграл от суммы равен сумме интегралов.
Интеграл Римана является частным случаем интеграла Стилтьеса для F(x)=x.
Рассмотрим два частных случая:
a. F(x) – ступенчатая функция, имеющая в точках xiскачки величины piи постоянная между этими точками. Приращения F(tk+1)-F(tk) на тех интервалах Dtk, которые не содержат точек разрыва функции F(x), равны нулю; если же точка xiявляется единственной точкой разрыва F(x), содержащейся в интервале Dtk, то разность F(tk+1)-F(tk) равна pi. Считая, что все точки разрыва изолированные, при переходе к пределу получим:  j(x)dF(x)=
j(x)dF(x)= 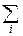 j(xi)pi.
j(xi)pi.
b. F(x) – дифференцируемая функция: существует производная F¢(x)=p(x). В интегральной сумме для интеграла Стилтьеса 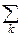 j(xk)[F(tk+1)-F(tk)] каждую из разностей [F(tk+1)-F(tk)] заменим по формуле Лагранжа: на каждом промежутке Dtkнайдётся такая точка hk, в которой F(tk+1)-F(tk)=F¢(hk)=
j(xk)[F(tk+1)-F(tk)] каждую из разностей [F(tk+1)-F(tk)] заменим по формуле Лагранжа: на каждом промежутке Dtkнайдётся такая точка hk, в которой F(tk+1)-F(tk)=F¢(hk)=
=p(hk)Dtk; пользуясь произволом в выборе точек xkиз промежутка Dtk, возьмём в каждом слагаемом интегральной суммы xk=hkи тогда сумма примет вид:
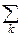 j(hk)p(hk)Dtk,
j(hk)p(hk)Dtk,
а это – ни что иное, как риманова интегральная сумма для функции j(x)p(x). Поэтому:
 j(x)dF(x)=
j(x)dF(x)=  j(x)p(x)dx.
j(x)p(x)dx.
В теории вероятностей интеграл Стилтьеса оказался удобным средством объединения случаев непрерывного и дискретного распределений в общем случае.
––²––
Вернёмся к изучению числовых характеристик случайных величин.
1°. Выше мы ввели понятие математического ожидания для дискретной и непрерывной случайных величин.
Пусть теперь X – случайная величина с функцией распределения F(x). Возьмём произвольную функцию j(x).
Назовём математическим ожиданием функции j от случайной величины X число Mj(X), определяемое равенством:
Mj(X)=  j(x)dF(x).
j(x)dF(x).
В частности, для непрерывной случайной величины с плотностью вероятности p(x) получаем:
Mj(X)=  j(x)p(x)dx,
j(x)p(x)dx,
а для дискретной случайной величины с распределением pk=P{X=xk}:
Mj(X)= 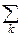 j(xk)pk.
j(xk)pk.
В случае, когда j(x)=x, последние три формулы принимают вид:
MX=  xdF(x) – в общем случае,
xdF(x) – в общем случае,
MX=  xp(x)dx – в непрерывном случае,
xp(x)dx – в непрерывном случае,
MX= 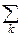 xkpk– в дискретном случае.
xkpk– в дискретном случае.
Формулы для непрерывного и дискретного случаев совпали с формулами для абсциссы центра тяжести распределения вероятностной массы, и тем самым оправдывается истолкование математического ожидания случайной величины X как среднего значения.
Для корректности определения математического ожидания следует обсудить вопрос о его существовании и единственности.
Вопрос о единственности Mj(X) возникает потому, что j(X) сама является случайной величиной со своей функцией распределения Fj(x) и в соответствии с нашим определением её математическое ожидание равно  xdFj(x).
xdFj(x).
Для однозначности определения необходимо выполнение равенства
 j(x)p(x)dx=
j(x)p(x)dx=  xdFj(x)
xdFj(x)
и такое равенство действительно можно доказать: оно даёт правило замены переменных в интеграле Стилтьеса. Мы здесь вынуждены принять его без доказательства.
Вопрос о существовании математического ожидания: ясно, что в непрерывном и дискретном случае любая ограниченная случайная величина имеет математическое ожидание. Если же X может принимать сколь угодно большие значения, то в дискретном случае сумма, определяющая MX, становится бесконечным рядом, а в непрерывном – интеграл становится несобственным, причём оба могут расходиться. Очевидно, в непрерывном случае достаточным условием существования среднего значения у случайной величины является
p(x)=O( 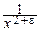 ) при x®±¥ (e>0),
) при x®±¥ (e>0),
а в дискретном случае:
xkpk=O( 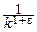 ) при k®¥ (e>0).
) при k®¥ (e>0).
Однако оба эти условия не являются необходимыми.
Легко также придумать примеры случайных величин, не имеющих среднего. Для непрерывного случая таким примером может служить распределение Коши. В дискретном подобный пример придумать ещё проще, если учесть, что вероятность pkможно приписать сколь угодно большим числам xk.
Если дана двумерная случайная величина (X, Y), то математическое ожидание функции j(X, Y) определяется равенствами
Mj(X, Y)= 
 j(x, y)p(x, y)dxdy – в непрерывном случае
j(x, y)p(x, y)dxdy – в непрерывном случае
(интеграл берётся по всей плоскости),
Mj(X, Y)= 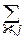 j(xi, yj)pij– в дискретном случае
j(xi, yj)pij– в дискретном случае
(сумма берётся по всем возможным значениям
двумерной случайной величины).
2°. Второй по важности числовой характеристикой случайной величины X служит её дисперсия DX. Дисперсией называется
DX=M[(X-MX)2]=  (x-MX)2dF(x),
(x-MX)2dF(x),
т. е. среднее значение квадрата отклонения случайной величины от её среднего. Эта формула в непрерывном случае переходит в
DX=  (x-MX)2p(x)dx,
(x-MX)2p(x)dx,
а в дискретном в:
DX= 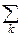 (xk-MX)2pk.
(xk-MX)2pk.
Если среднее есть не у всех случайных величин, то дисперсия и подавно. В дальнейшем все теоремы о MX и DX без особых оговорок формулируются лишь для тех X, которые их имеют.
Размерность дисперсии равна квадрату размерности случайной величины X. Поэтому иногда удобно вместо DX рассматривать величину sX= 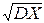 , называемую средним квадратичным отклонением случайной величины X или просто стандартом.
, называемую средним квадратичным отклонением случайной величины X или просто стандартом.
Дисперсия и стандарт мыслятся как меры разброса значений случайной величины вокруг её среднего.
3°. Докажем несколько простых утверждений:
Математическое ожидание постоянной C равно C: MC=C.
Постоянный множитель можно выносить за знак математического ожидания:
M(CX)=CMX.
Дисперсия постоянной равна нулю: DC=0.
Постоянный множитель выносится за знак дисперсии в квадрате:
D(CX)=C2DX.
Постоянную C можно рассматривать как частный случай дискретной случайной величины, принимающей единственное значение C с вероятностью, равной 1. Поэтому MC=C×1=C.
Свойство M(CX)=CMX следует из определения математического ожидания как предела интегральных сумм: постоянный множитель можно выносить за знак суммы и знак интеграла.
О дисперсии:
DC=M[(C-MC)2]=M[(C-C)2]=M0=0;
D(CX)=M[(CX-M(CX))2]=M[(CX-CM(X))2]=
=M[C2(C-MC)2]=C2×M[(X-MX)2]=C2DX.
4°. Математическое ожидание суммы случайных величин равно сумме их математических ожиданий:
M(X+Y)=MX+MY.
Докажем эту теорему отдельно для непрерывного и дискретного случая.
a. Непрерывный случай. Пусть p(x, y) – двумерная плотность вероятности.
Согласно определению математического ожидания функции от двумерной случайной величины:
M(X+Y)= 
 (x+y)p(x, y)dxdy.
(x+y)p(x, y)dxdy.
Представляя двойной интеграл как сумму двух повторных и выбирая соответствующий порядок интегрирования в слагаемых, имеем:
M(X+Y)=  xdx
xdx  p(x, y)dy+
p(x, y)dy+  ydy
ydy  p(x, y)dx=
p(x, y)dx=
=  xpX(x)dx+
xpX(x)dx+  ypY(y)dy=MX+MY.
ypY(y)dy=MX+MY.
b. Дискретный случай.
M(X+Y)= 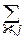 (xi+yj)pij.
(xi+yj)pij.
Представляем двойную сумму как две повторные:
M(X+Y)= 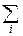 xi
xi 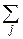 pij+
pij+ 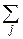 yi
yi 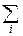 pij=
pij= 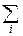 xipi+
xipi+ 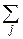 yjpj=MX+MY.
yjpj=MX+MY.
Аналогично эту теорему можно доказать для смешанного случая. Общая же формулировка потребовала бы введения двумерного интеграла Стилтьеса.
5°. Предыдущая теорема естественно обобщается на сумму n слагаемых:
M 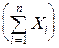 =
= 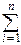 MXi.
MXi.
Как частный случай применения этой формулы отметим следующую задачу: имеются события A1, A2, ¼ , An, их вероятности соответственно равны p1, p2, ¼ , pn. Спрашивается, чему равно ожидаемое число событий A1, A2, ¼ , An, которые произойдут в опыте? Определим вспомогательные случайные величины Xiравенствами:
|
0, если событие Aiне произошло.
Всего в опыте происходит 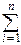 Xi событий, а ожидаемое число равно
Xi событий, а ожидаемое число равно
M 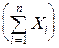 =
= 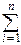 MXi=
MXi= 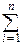 pi.
pi.
6°. Ещё одна формула для дисперсии: DX=M(X2)-M2(X).
Действительно, в силу теорем 3° и 4° имеем:
DX=M[(X-MX)2]=M(X2)-MX×MX+M[M(X)2]=
=M(X2)-2.M2(X)+M2(X)=M(X2)-M2(X).
В частности, если MX=0, то DX=M(X2).
7°. Нормированной случайной величиной X*назовём:
X*= 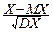 .
.
Это – безразмерная случайная величина, причём:
a) MX*=0, b) M(X*2)=1, c) DX*=1.
Действительно, по теореме 3° и 4°:
MX*=M( 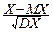 )=
)= 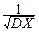 (MX-MX)=0,
(MX-MX)=0,
M(X*2)=M[ 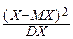 ]=
]= 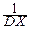 M[(X-MX)2]=
M[(X-MX)2]=