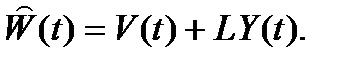Редуцированные наблюдающие устройства
Рассмотренное выше структура наблюдающего устройства обладает некоторой избыточностью. Избыточность выражается в том, что наблюдающее устройство оценивает весь вектор переменных состояния X(t), хотя часть координат вектора состояния могут быть непосредственно измерены. Эту избыточность можно устранить путем синтеза редуцированного наблюдающего устройства, порядок которого меньше, чем порядок заданного динамического объекта.
Пусть измерению доступны первые m координат вектора состояния X(t). Тогда вектор переменных состояния можно представить следующим образом
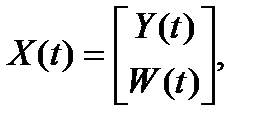
где Y(t) – вектор размерности m (измеряемые координаты), W(t) – вектор размерности n – m (неизмеряемые координаты вектора состояния).
Тогда уравнение выхода для объекта управления можно представить следующим образом
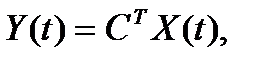
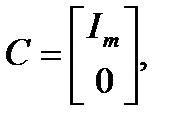
где Im – единичная матрица размера m× m, 0 – нулевая матрица.
В уравнении
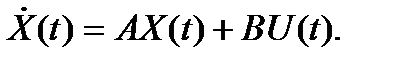
Матрицу А и вектор В представим в блочной форме:
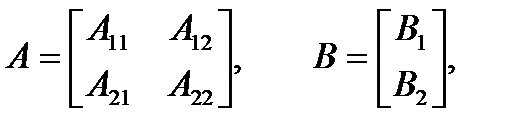
где A11 – матрица размера m× m, A12 – матрица размера m× (n – m), A21 – матрица размера (n – m) × m, A22 – матрица размера (n – m) ×(n – m), вектора В1 и В2 имеют размер m и n – m.
Тогда уравнение состояния можно переписать следующим образом
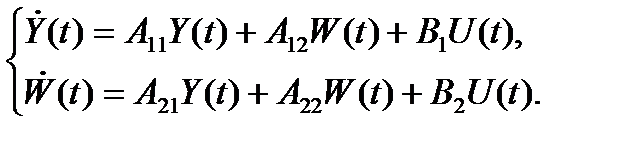
Этим уравнениям соответствует структурная схема, приведенная на рис. 2.10
| B2 |
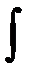 |
| A12 |
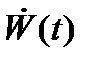 |
| U(t) |
| B1 |
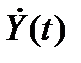 |
| Y(t) |
| A11 |
| A22 |
| W(t) |
| A21 |
| Z(t) |
| ∫ |
∫
Рис. 2.10. Блочное представление уравнения состояния.
Идея синтеза редуцированного наблюдающего устройства заключается в следующем. Так как вектор Y(t) доступен непосредственному измерению, то полагаем, что можно каким-либо способом вычислить и его производную по времени. Ввиду того, что управляющая функция также доступна измерению, то согласно уравнению можно вычислить вектор
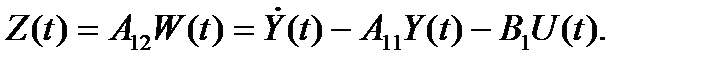
Рассмотрим затем уравнение
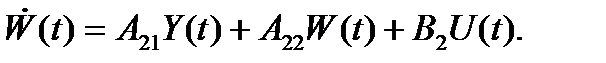
Это уравнение можно рассматривать как модель объекта с вектором состояния W(t).
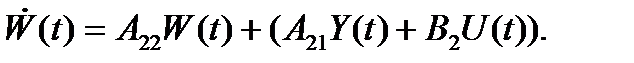
Слагаемое в скобке будем рассматривать в качестве внешнего воздействия.
Основной теоретической базой для синтеза редуцированного наблюдателя является утверждение: «Если система A, C обладает свойством наблюдаемости, то свойствами наблюдаемости обладает и подсистема A22, A12».
Рассмотрим динамический объект, описываемый системой уравнений:
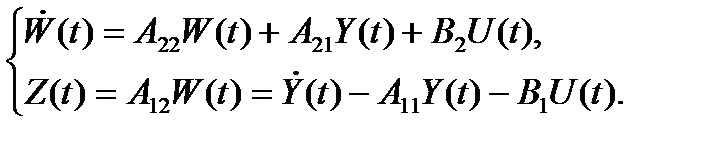
Первое из этих уравнений описывает динамику объекта (рис. 2.11), а второе является уравнением выхода.
| B2 |
 |
| A21 |
| Y(t) |
| Z(t) |
| A12 |
| A22 |
| W(t) |
| U(t) |
Рис. 2.11. Структура динамического объекта
Для того, чтобы получить математическую модель редуцированного наблюдающего устройства воспользуемся общим уравнением наблюдающего устройства полного порядка
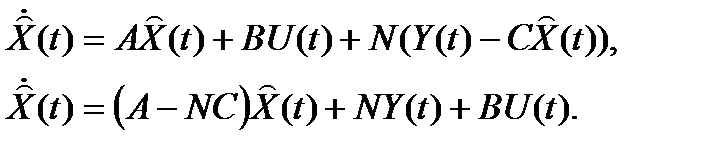
Для редуцированного наблюдающего устройства матрице A будет соответствовать A22, матрице C – A12, и матрице N – матрица L, которой соответствуют коэффициенты обратных связей редуцированного наблюдающего устройства.
Таким образом, получаем оценку вектора состояния динамического объекта
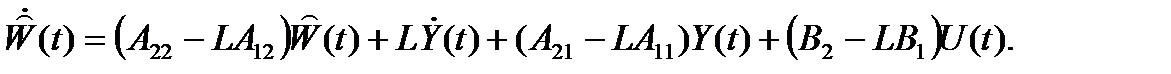
Структурная схема редуцированного наблюдающего устройства показана на рис. 2.12.
| A21–LA11 |
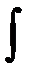 |
| Y(t) |
| B2–LB1 |
| U(t) |
| d/dt |
| L |
| A22–LA12 |
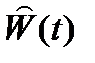 |
Рис. 2.12. Редуцированное наблюдающее устройство
Для того, чтобы избавиться от операции дифференцирования, можно ввести в рассмотрение вектор состояния наблюдающего устройства размером (n – m):
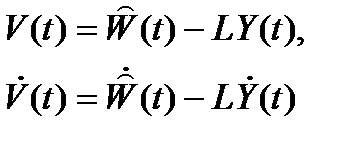
Тогда можно записать (подставляем 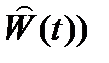 ):
):
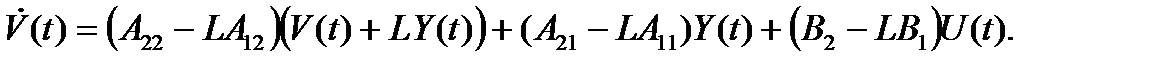
Получается следующая структурная схема (рис. 2.13).
| A21–LA11 |
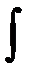 |
| Y(t) |
| B2–LB1 |
| U(t) |
| L |
| A22–LA12 |
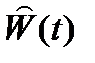 |
| V(t) |
Рис.
Рис. 2.13. Вариант редуцированного наблюдающего устройства
Последнее уравнение можно перегруппировать:
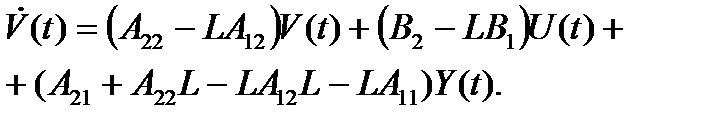
Затем можно найти оценку состояния: