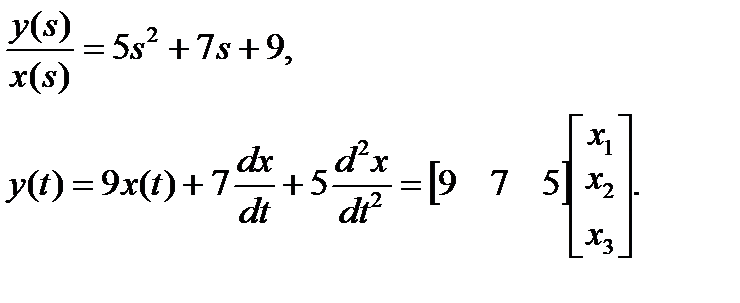Модели в пространстве состояний

Практически все динамические объекты могут быть описаны с помощью дифференциальных уравнений.

Метод пространства состояний позволяет исследовать системы во временной области. Преимущества этого подхода обусловлены тем, что он позволяет единообразно исследовать и одномерные, и многомерные, и линейные, и нелинейные системы.

Состояние системы – это совокупность таких переменных, знание которых позволяет, при известном входе и известных уравнениях динамики, описать будущее состояние системы и значение ее выхода.

Рассмотрим примеры, иллюстрирующие составление уравнений в переменных состояния.

Пример 1.1. Тележка на колесах массой M, перемещающаяся под воздействием силы f(t) вдоль оси x с коэффициентом трения k (рис. 1.1).

m

f(t)

x

Рис.1.1. Тележка на колесах

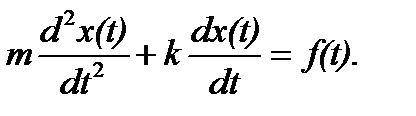
Введем переменные состояния:

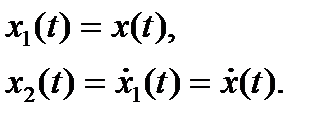
Тогда

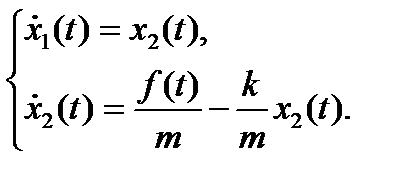
В матричной записи:

Пример 1.2. Механическая система с линейным перемещением (рис. 1.2).

m

fПР= –k1y(t)

y

fТР= –k2dy(t)/dt

f(t)

Рис.1.2. Механическая система с линейным перемещением

На тело массой m действует три силы: внешняя сила f(t), сила трения f_ТР (t), пропорциональная скорости с коэффициентом k₂, и сила упругости f_ПР(t), пропорциональная перемещению вдоль оси y(t) с коэффициентом k₁.

Под действием этих сил тело движется согласно закону Ньютона, который гласит, что сумма сил, действующих на тело, равна произведению массы тела на его ускорение:

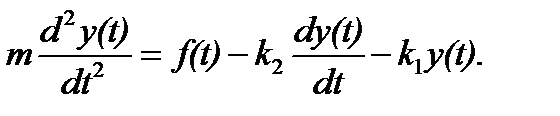
а передаточная функция (ПФ) равна

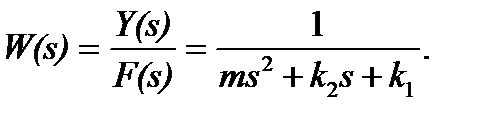
Это выражение определяет зависимость положения y(t) от действующей силы f(t).

Допустим, что нам нужна также информация о скорости dy(t)/dt. Введём следующие переменные:

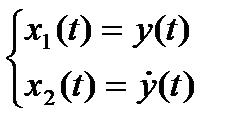
Далее можем записать:

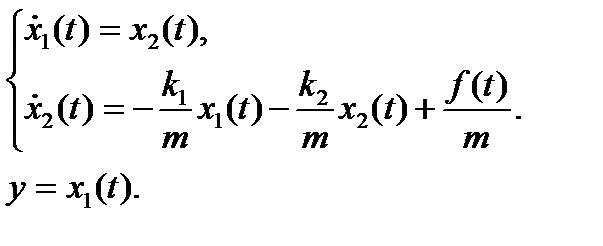
Представим эту систему уравнений в векторно-матричной форме:

.

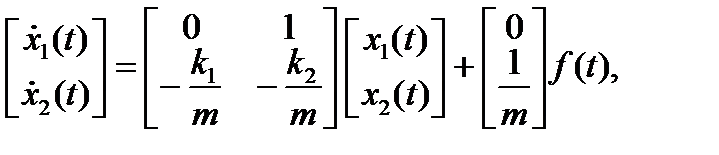
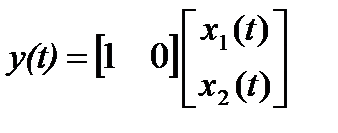Пример 1.3. Рассмотрим систему, описываемую дифференциальными уравнениями:

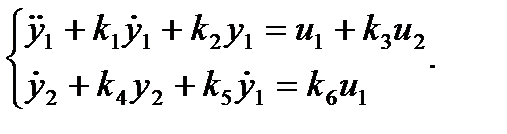
где u₁ и u₂ - входные переменные, а y₁ и y₂ - выходные переменные.

Выберем переменные состояния:

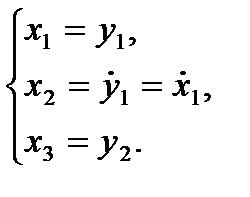
Тогда:

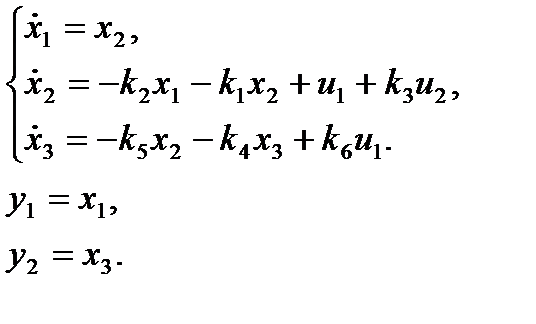
Эти уравнения можно записать в векторно-матричной форме:

.

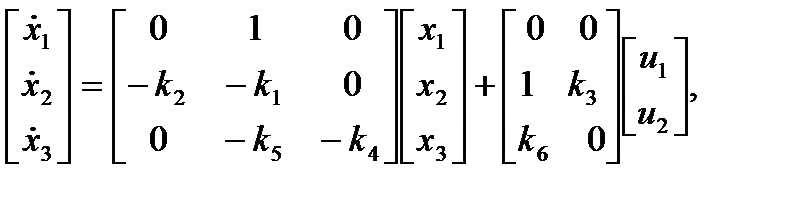
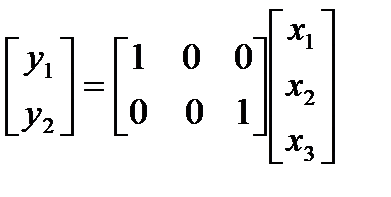Уравнения состояний линейной стационарной системы имеют следующий общий вид:

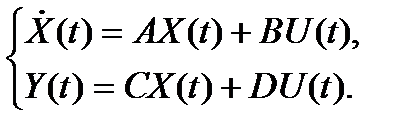
где X – вектор-столбец состояния [n ´ 1]; А – матрица коэффициентов объекта [n ´ n]; В – матрица входа [n ´ m]; U – вектор входа (управления) [m ´ 1]; Y – вектор выхода [k ´ 1]; С – матрица выхода [k ´ n]; D – матрица влияния входа непосредственно на выход системы [k ´ m].

Уравнениям состояния соответствует структурная схема, показанная на рис. 1.3.

Y(t)

B

ò

C

A

U(t)

X(t)

D

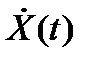Рис. 1.3. Структура системы в пространстве состояний

На практике часто рассматриваются скалярные системы (с одним входом и одним выходом). Матрица D обычно нулевая. Тогда можно записать уравнения состояния в развернутом виде:

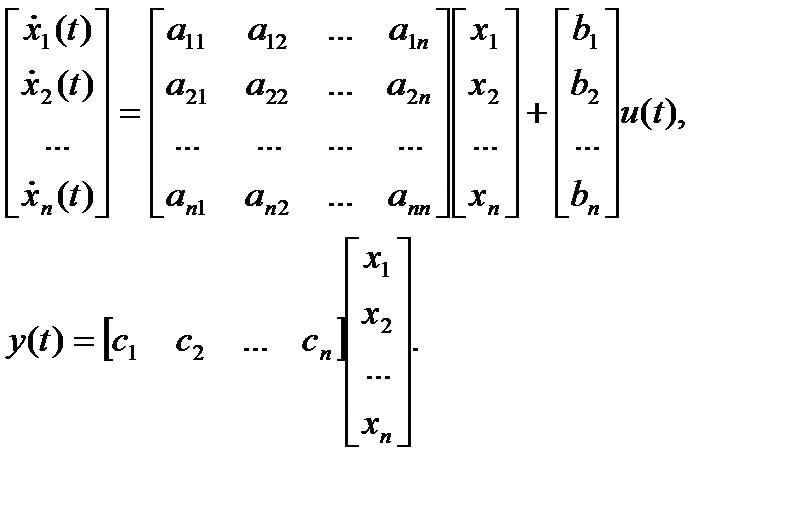
Имея описание скалярной системы в виде ПФ, можно легко получить описание в пространстве состояний:

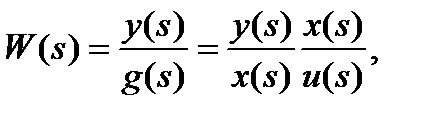
где y(s), u(s), x(s) - выход, вход и состояние системы.

Первой дроби соответствует уравнение выхода, а второй – уравнение состояния.

Пример 1.4. Имеется ПФ объекту управления:

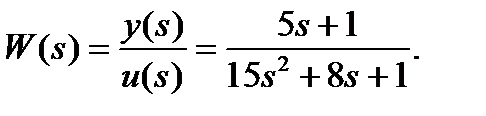
Требуется получить уравнения состояния.

Решение.

Уравнение состояния:

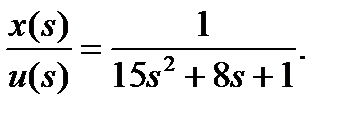
Тогда

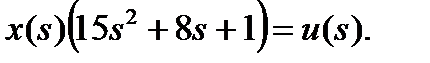
Переходя во временную область, можем записать:

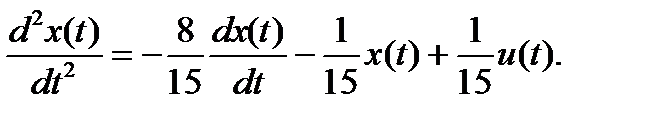
Выбираем переменные состояния: x₁ = x; x₂(t) = dx/dt, тогда можно записать

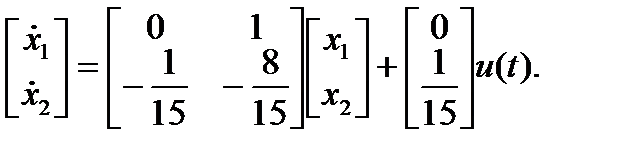
Уравнения выхода:

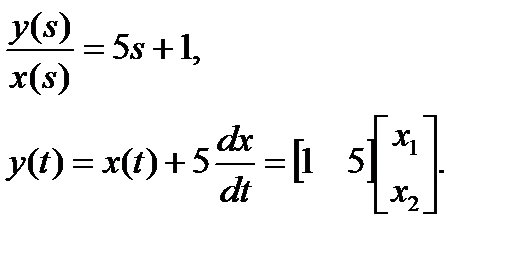
Пример 1.5. Рассмотрим систему 3-го порядка.

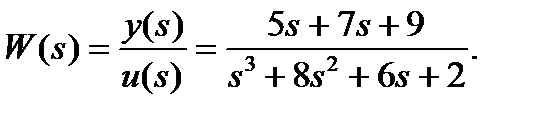
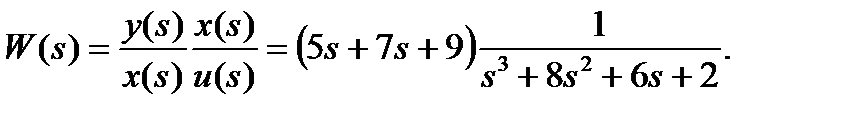
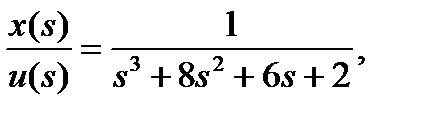
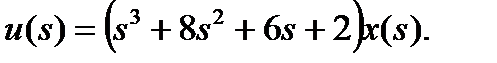
Переходя во временную область:

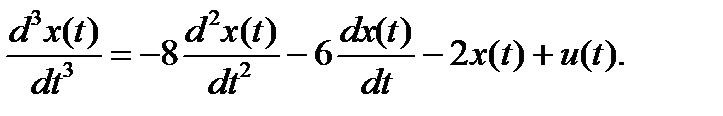
Вводим переменные состояния:

x₁ = x, x₂(t) = dx/dt, x₃(t) = d²x/dt².

Получаем уравнение состояния

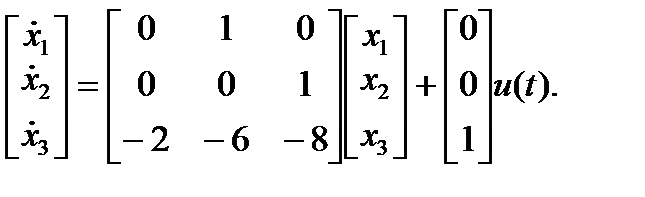
Уравнение выхода