Метод пространства состояний

Бураков М.В.

Д79 Теория автоматического управления: учеб. пособие. Часть 2/ М. В. Бураков;– СПб.: ГУАП, 2014. -258 с.: ил.

ISBN

Учебное пособие предназначено для подготовки бакалавров и магистров по направлению 220400 «Управление в технических системах», а также студентов других специальностей, изучающих дисциплины «Теория автоматического управления» и «Основы теории управления».

УДК 681.5

ББК

Б

ISBN © Санкт-Петербургский государственный

университет аэрокосмического

приборостроения (ГУАП), 2014

© М. В. Бураков, 2014

©

Оглавление

1.	МЕТОД ПРОСТРАНСТВА СОСТОЯНИЙ
	ЗАКЛЮЧЕНИЕ
	Библиографический список

Введение

Метод пространства состояний

Линеаризация в пространстве состояний

Как было показано выше, описание в пространстве состояний можно получить, выполняя преобразование ПФ объекта. Однако возможен и другой путь – на основании линеаризации исходных нелинейных уравнений объекта.

Рассмотрим нелинейное уравнение состояния

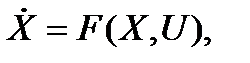
где X и F – векторы размерностью [n × 1], U – вектор размерностью [r × 1].

Пусть X₀ – рабочая точка нелинейной системы n-го порядка, а U₀ – постоянное значение входа, соответствующее этой точке.

Предположим, что появляется отклонение:

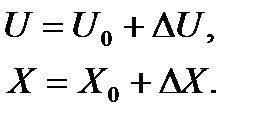
Тогда

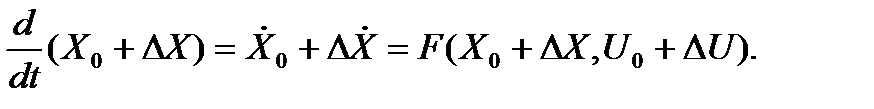
Для j-й компоненты вектора X можно записать:

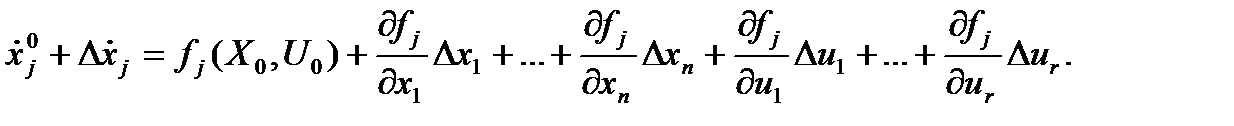
Поскольку

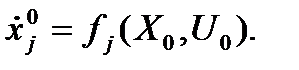
Получаем

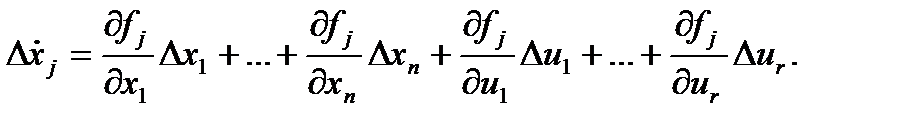
Для всех компонентов вектора X:

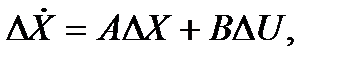
где

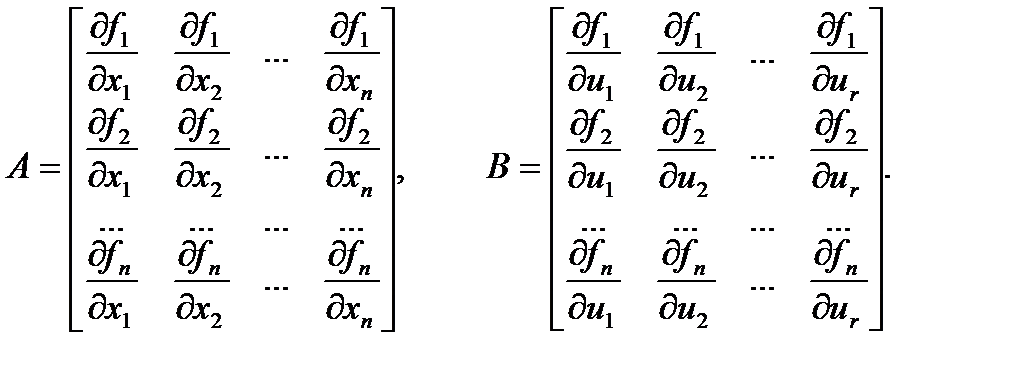
Эти матрицы называются якобианами.

Для удобства записи обычно вместо DX используют X, и вместо DU – U:

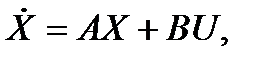
где под X понимаются отклонения переменных состояния от их установившихся значений, а под U – отклонения входных воздействий.

Рассмотрим пример линеаризации нелинейной системы.

Пусть дано нелинейное дифференциальное уравнение 2-го порядка.

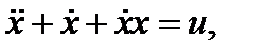
где все переменные являются функциями времени.

Введем переменные состояния:

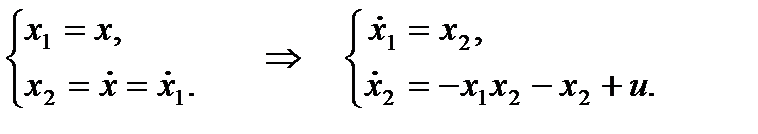
Нелинейные уравнения состояния примут вид:

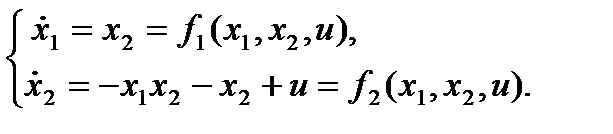
В векторной форме:

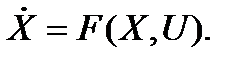
Рассмотрим аппроксимацию этих нелинейных уравнений в рабочей точке X₀, U₀.

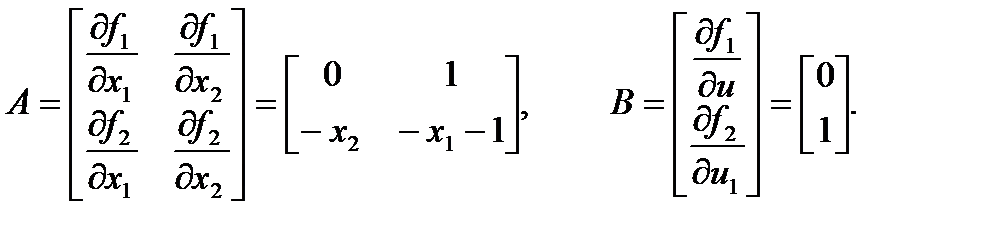
1.2. Структурные преобразования в пространстве состояний

Рассмотрим соединение двух подсистем, описываемых в пространстве состояний, в одну. Предполагается, что обе подсистемы описываются соотношениями:

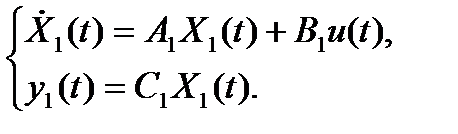
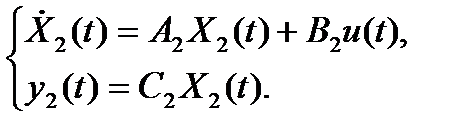
Параллельное соединение подсистем показано на рис. 1.4.

A1, B1, C1

A2, B2, C2

y

y1

y2

u

Рис. 1.4. Параллельное соединение подсистем

Для параллельного соединения:

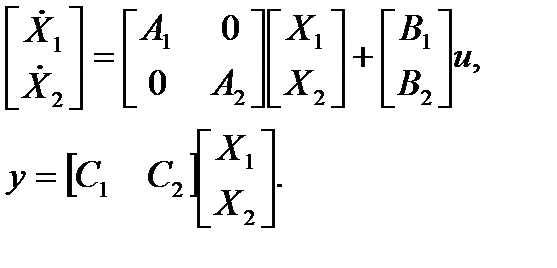
Последовательное соединение подсистем показано на рис. 1.5.

A1, B1, C1

A2, B2, C2

u1

y1 = u2

y2

Рис. 1.5. Последовательное соединение подсистем

Для последовательного соединения:

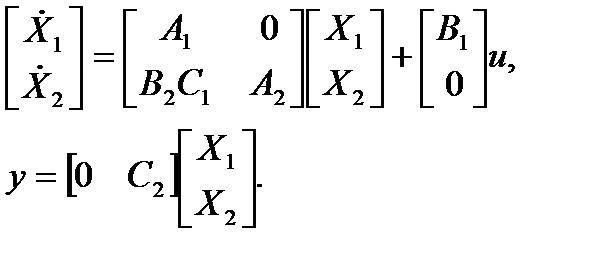
Соединение с обратной связью показано на рис. 1.6.

A1, B1, C1

A2, B2, C2

y1 = y

u2 = y1

u

u1

±

Рис. 1.6. Cоединение подсистем с обратной связью

Для рис. 1.6 справедливо

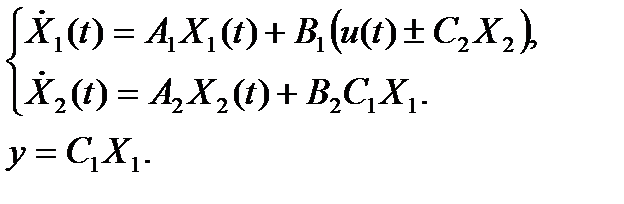
В матричном виде:

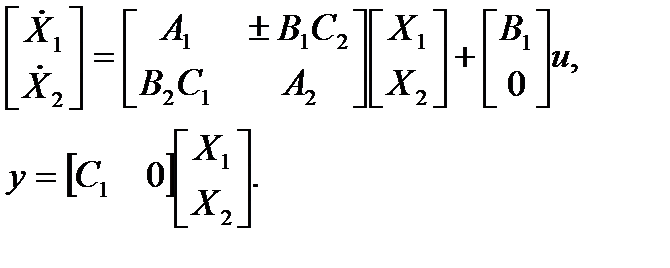
Модальный синтез

Модальный синтез предполагает формирование таких обратных связей по состоянию, при которых обеспечивается заданное расположение полюсов замкнутой системы.

Рассмотрим уравнения состояния замкнутой системы

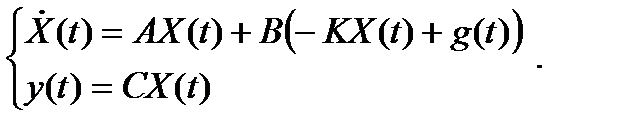
На рис. 2.1 приведена структура, соответствующая этим уравнениям.

g(t)

Y(t)

B

C

A

u(t)

X(t)

K

ò

dX(t)/dt

Рис. 2.1. Система с обратной связью по состоянию

Свободное движение системы (при g(t)= 0) описывается выражением:

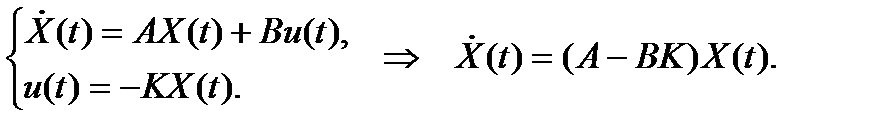
где K – вектор коэффициентов обратной связи.

Основная теорема модального управления гласит, что если линейная динамическая система является управляемой, то линейная обратная связь может быть выбрана таким образом, что матрица (А – ВK) будет иметь желаемый спектр (желаемое расположение полюсов замкнутой системы).

При доказательстве этой теоремы используется каноническая форма управляемости. Рассмотрим одномерную систему с вектором обратной связи

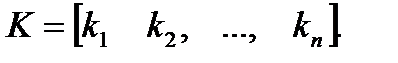
Заданному спектру соответствует характеристический полином замкнутой системы

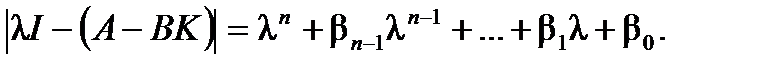
Этому полиному можно поставить в соответствие каноническую форму матрицы замкнутой системы

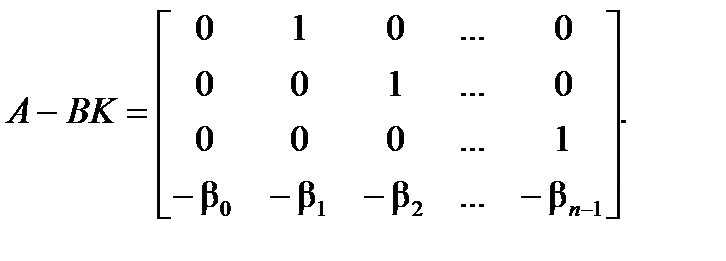
Рассматривая канонические формы матриц А и В исходной системы, можно записать:

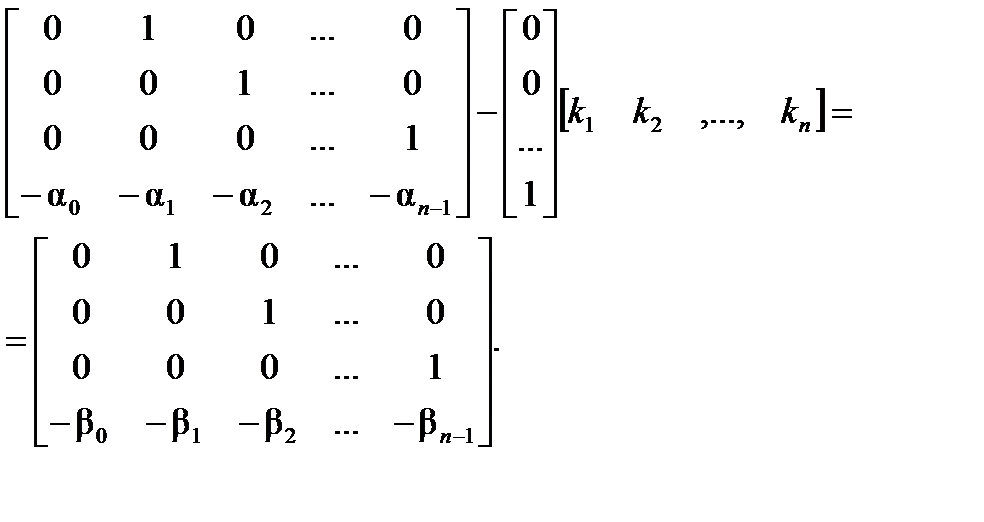
Откуда следует:

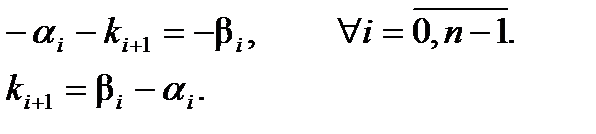
Последняя формула справедлива при любых параметрах, поэтому теорему можно считать доказанной.

Пример 2.6. Модальный синтез для системы со скалярным входом.

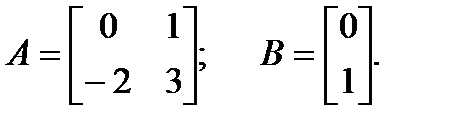
Матрица управляемости

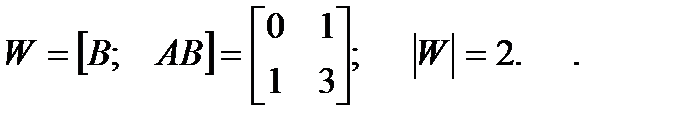
Определитель не равен нулю, следовательно, система является полностью управляемой.

Характеристическое уравнение:

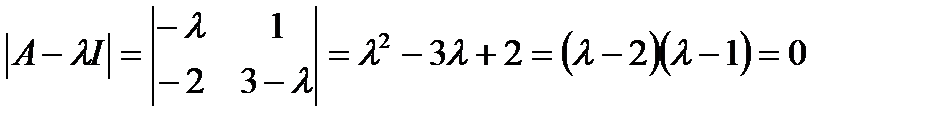
Коэффициенты уравнения α₀ = 2, α₁ = –3.

Оба полюса положительные (λ₁=2, λ₂=1), следовательно, система является неустойчивой.

Зададим желаемые полюса замкнутой системы:

λ₁* = –1, λ₂* = –3.

Характеристическое уравнение желаемой замкнутой системы имеет вид:

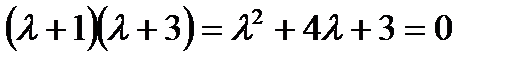
Коэффициенты уравнения β₀ = 3, β₁ = 4.

Таким образом, коэффициенты обратной связи:

k₁ = β₀ – α₀ = 3 – 2 = 1,

k₂ = β₁ – α₁ = 4 – (–3) = 7.

Уравнения состояния:

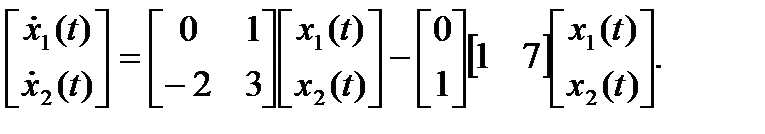
Этим уравнениям соответствует структурная схема, показанная на рис. 2.2.

g(t)

u(t)

ò

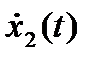ò

–2

x1(t)

x2(t)

Рис. 2.2. Пример регулятора по состоянию

Формула Аккермана

Таким образом, для решения задачи модального управления можно перевести модель произвольной структуры в каноническую форму управляемости, после чего с помощью уравнения получить коэффициенты обратной связи. Однако в реальной системе желательно использовать переменные состояния, отражающие физическую сторону протекающих процессов, а не абстрактные переменные состояния канонической формы, которые могут быть недоступны для измерения. Аккерманом была предложена формула, позволяющая с помощью преобразования подобия перевести модель произвольной структуры в каноническую форму управляемости, определить искомые коэффициенты K, а затем пересчитать полученное решение применительно к исходной структуре.

Если задан желаемый характеристический полином замкнутой системы

q(s) = ,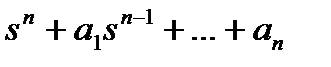

то формула Аккермана имеет вид:

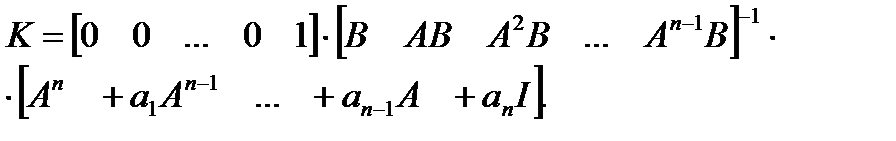
Пример 2.7. Пусть система описывается матрицами

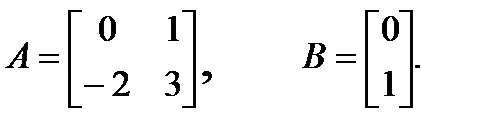
Желаемые полюса заданы вектором

.

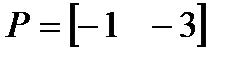Требуется найти коэффициенты обратной связи.

Характеристический полином желаемой замкнутой системы имеет вид:

q(s) = ,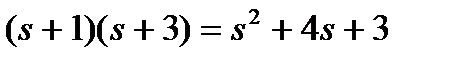

т. е. a₂=3; a₁=4.

Формула Аккермана:

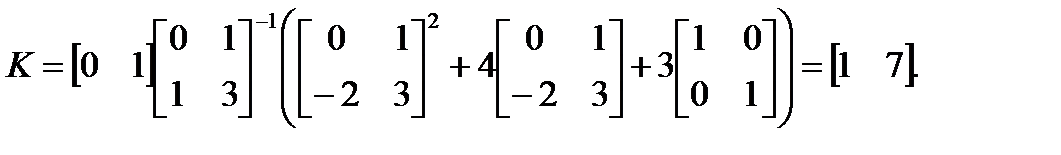
Этот результат совпадает с полученным ранее.

Пример 2.8. Дана передаточная функция объекта:

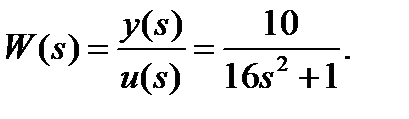
Найти коэффициенты обратной связи, обеспечивающие заданные значения корней характеристического полинома замкнутой системы:

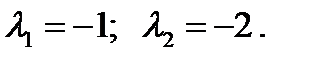
Запишем уравнения в канонической форме управляемости

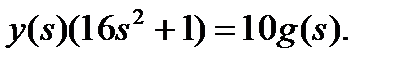
Здесь, очевидно,

b₂=0, b₁=0, b₀=10.

a₂=16, a₁=0, a₀=1.

Тогда

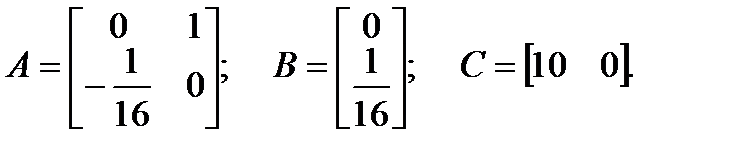
Характеристическое уравнение желаемой замкнутой системы имеет вид:

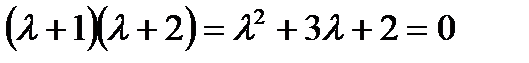
Коэффициенты уравнения α₀ = 2, α₁ = 3.

Записываем формулу Аккермана

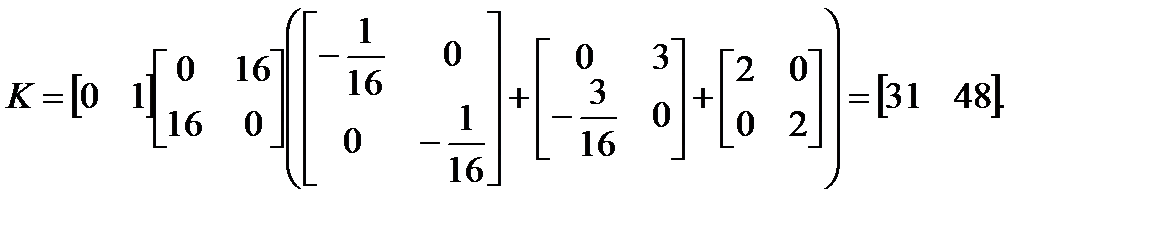
Наблюдающие устройства

Метод модального управления предполагает, что все компоненты вектора состояния X могут быть измерены, но на практике некоторые компоненты могут быть неизвестны по одной из двух причин:

- измерительных приборов может быть недостаточно;

- некоторые компоненты вектора X могут не иметь физического смысла.

Однако если система является наблюдаемой, то все компоненты вектора X могут быть восстановлены по наблюдениям вектора Y.

Иначе говоря, если система наблюдаемая, то все компоненты вектора состояния вносят свой вклад в выходной сигнал системы.

В настоящее время известны два подхода косвенного определения компонент вектора состояния управляемого объекта, недоступных прямому измерению. Это фильтр Калмана и наблюдающее устройство Люинбергера.

При использовании фильтров Калмана детерминированный подход к рассмотрению анализируемой системы автоматического управления заменяется стохастическим. Областью применения таких наблюдающих устройств являются в основном системы управления сложными электромеханическими устройствами.

При анализе детерминированных механических систем задача оценки всех переменных состояния управляемого объекта может быть решена с помощью более простого устройства, называемого наблюдающим устройством Люинбергера. Входными сигналами для этого устройства служат доступные измерению выходные координаты объекта, а также поступающие на него входные воздействия.

Наблюдающие устройства Люинбергера представляют собой динамическую систему, которая является моделью объекта:

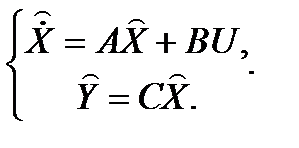
где 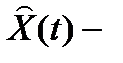оценка состояния объекта, 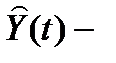оценка выхода.

Рассмотрим ошибку состояния и выхода:

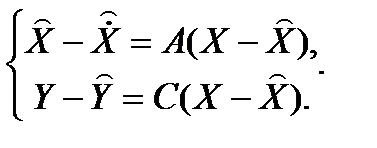
Если начальное состояние объекта и модели совпадают, и модель адекватна объекту, то можно полагать в любой момент времени, что

.

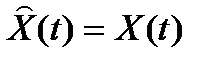Общая структура системы управления с наблюдателем показана на рис. 2.7.

Регулятор

Объект

Наблюдатель

G(t)

U(t)

X(t)

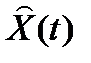Y(t)

Y(t)

Измеритель

Рис. 2.7. Система управления с наблюдателем

Однако практически добиться полной адекватности объекта и модели невозможно, трудно добиться и полного равенства начальных условий. Поэтому на практике можно рассчитывать лишь на выполнение условия

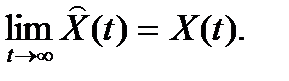
Подобным свойством обладают так называемые асимптотические наблюдающие устройства.

Асимптотическое наблюдающее устройство использует обратную связь по ошибке восстановления вектора состояния, так что работа наблюдающего устройства описывается уравнением

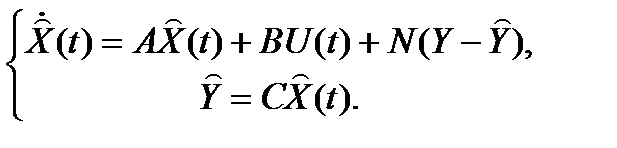
где N – матрица параметров наблюдающего устройства.

Можно записать

.

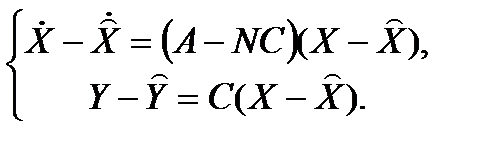Если ввести обозначение для ошибки по состоянию

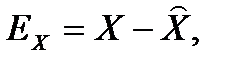
то получаем

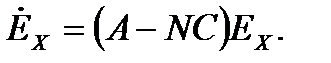
Таким образом, если собственные числа матрицы A – NC имеют отрицательную вещественную часть, то с течением времени ошибка состояния уменьшиться до нуля. Соответственно, при синтезе наблюдателя нужно выбрать положение корней характеристического уравнения:

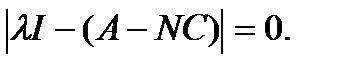
Рассмотрим влияние наблюдателя на динамику системы с обратной связью. Система с наблюдателем описывается уравнениями

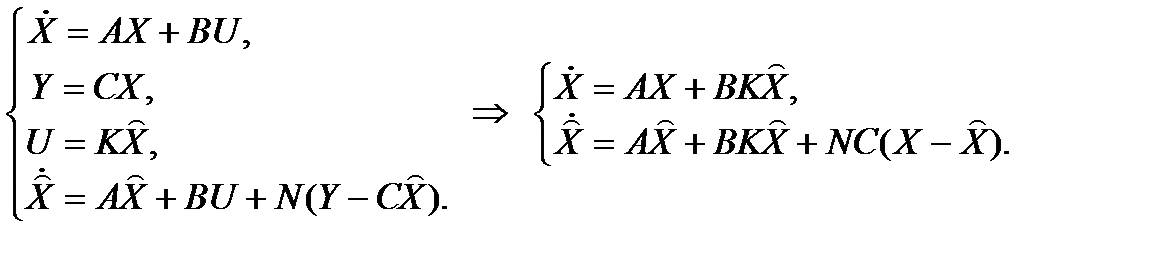
Структурная схема системы с наблюдающим устройством показана на рис. 2.9.

B

C

A

X(t)

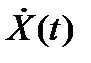Y(t)

N

g(t)

B

C

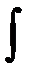A

K

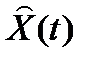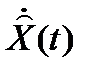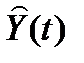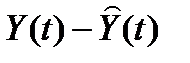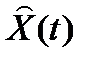Регулятор

Наблюдатель

Объект

U(t)

Рис. 2.9. Система с наблюдающим устройством

Рассмотрим систему

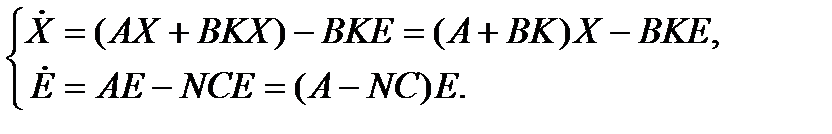
Таким образом, уравнения динамики системы с наблюдающим устройством можно записать в матричной форме

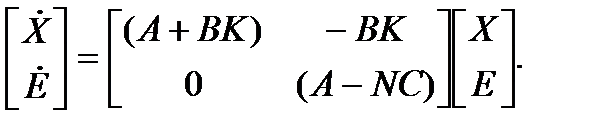
Характеристическое уравнение этой системы имеет вид:

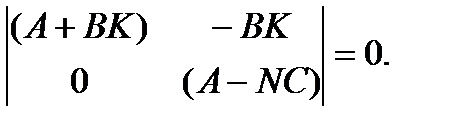
Собственные значения блочной треугольной матрицы совпадают с собственными значениями диагональных блоков

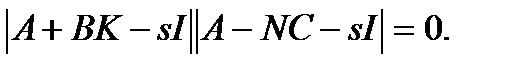
Это уравнение имеет 2n корней, из которых n корней заданы условиями модального синтеза и еще n являются корнями наблюдателя. Таким образом, оказывается, что параметры наблюдателя и параметры регулятора могут рассчитываться независимо.

Понятно, что процессы в наблюдателе должны протекать более быстро, чем переходный процесс в системе. Эмпирически установлено, что наблюдатель должен обладать быстродействием, в 2 - 4 раза превышающим быстродействие системы.

При синтезе наблюдателя удобно использовать каноническую форму наблюдаемости.

Пример Рассмотрим объект 3-го порядка

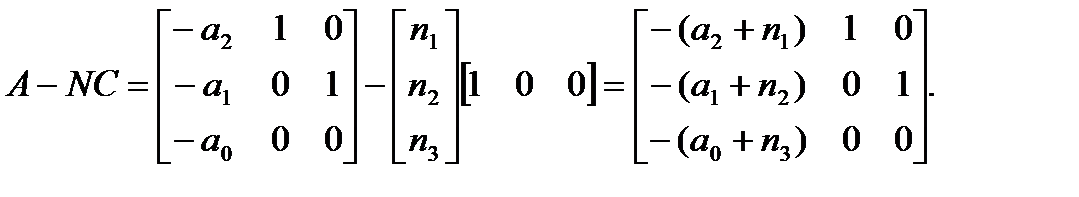
Характеристическое уравнение принимает вид:

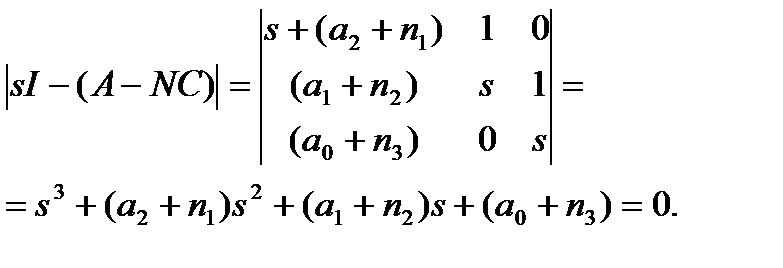
Далее надо рассмотреть характеристический полином желаемой замкнутой системы

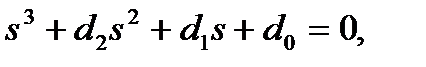
и, приравняв коэффициенты при одинаковых степенях s, найти параметры наблюдателя:

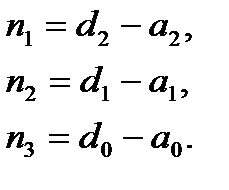
Пример 2.12. Объект управления задан матрицами в канонической форме наблюдаемости

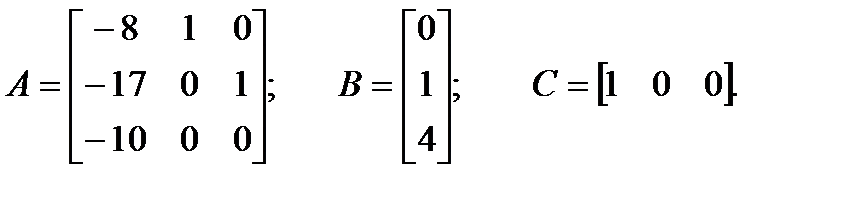
Требуется построить наблюдающее устройство.

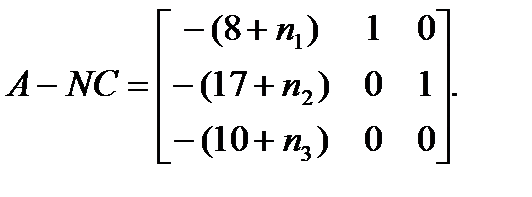
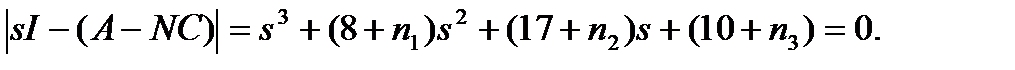
Допустим, что выбран следующий желаемый характеристический полином

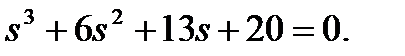
Тогда параметры наблюдателя равны:

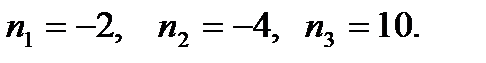
В рассмотренном примере синтез наблюдателя выполнен методом модального управления.

Второй способ синтеза наблюдателя – это собственно синтез наблюдателя Люенбергера.

Введём n-мерный вектор состояния наблюдателя V, связанный с X соотношением

,

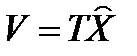где T – не особая матрица размерности n×n. Из системы уравнений

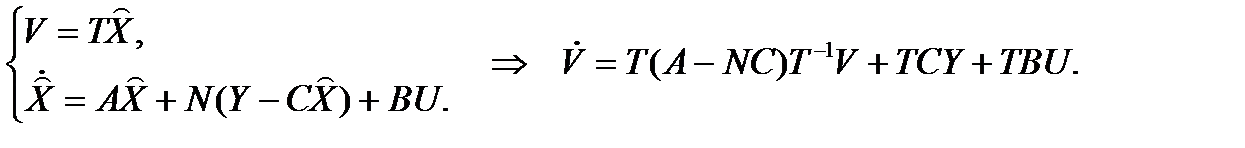
Введем обозначение

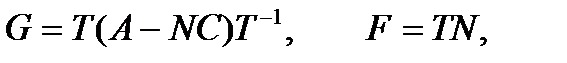
где N – неизвестная матрица.

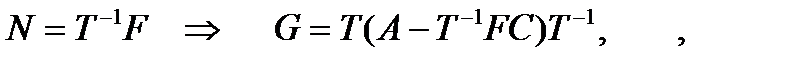
откуда следует

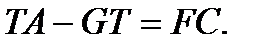
Таким образом, наблюдатель Люенбергера описывается системой уравнений

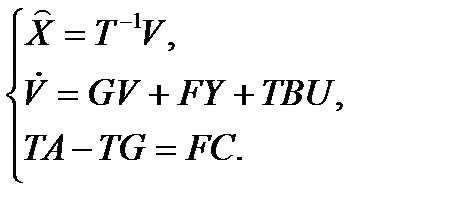
Пример.

Пример 2.22. Объект управления задан уравнениями в пространстве состояний:

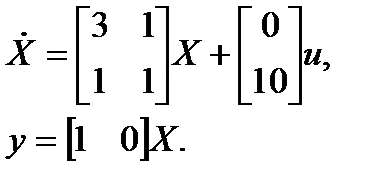
Требуется построить наблюдатель Люинбергера.

На первом шаге проверяется наблюдаемость объекта:

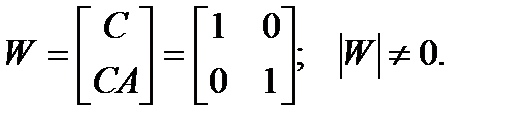
Допустим, что при модальном синтезе выбраλно положение полюсов замкнутой системы: λ₁ = λ₂ = –1. Матрица G описывает динамику наблюдателя, она должна иметь собственные числа, находящиеся левее на комплексной плоскости. Например

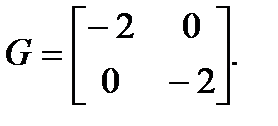
Матрица F выбирается из условий управляемости наблюдателя. Например:

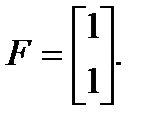
Затем необходимо решить уравнение:

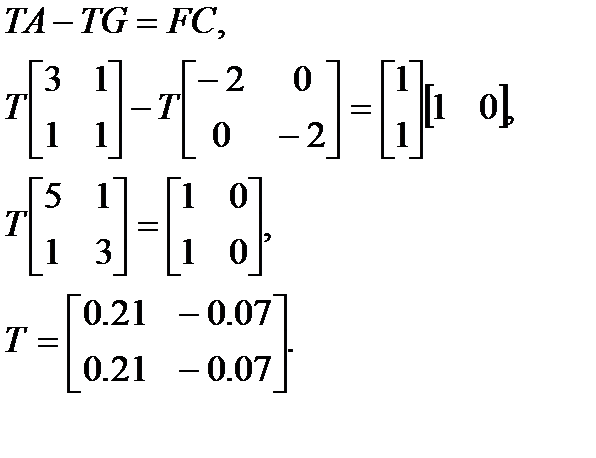
Бураков М.В.

Д79 Теория автоматического управления: учеб. пособие. Часть 2/ М. В. Бураков;– СПб.: ГУАП, 2014. -258 с.: ил.

ISBN

Учебное пособие предназначено для подготовки бакалавров и магистров по направлению 220400 «Управление в технических системах», а также студентов других специальностей, изучающих дисциплины «Теория автоматического управления» и «Основы теории управления».

УДК 681.5

ББК

Б

ISBN © Санкт-Петербургский государственный

университет аэрокосмического

приборостроения (ГУАП), 2014

© М. В. Бураков, 2014

©

Оглавление

1.	МЕТОД ПРОСТРАНСТВА СОСТОЯНИЙ
	ЗАКЛЮЧЕНИЕ
	Библиографический список

Введение

Метод пространства состояний