Wall Street: самая большая игра

Для того чтобы проиллюстрировать как применение критерия Кэлли, так и объёмы рынков ценных бумаг, мы вернемся к изучению корреляционного эффекта в Примере 6.2. Будем рассматривать более симметричную и эстетически более приемлемую пару ставок U₁ и U₂, с объединенным распределением, данным в Таблице 7.1

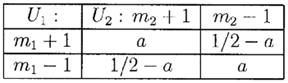ТАБЛИЦА 7.1 Объединенное распределение U₁ и U₂

Очевидно 0 £ a £ ½ и Cor(U₁,U₂) = Cor(U₁,U₂) =4a – 1 увеличивается от –1 до 1 при увеличении a от 0 до ½. Нахождение решения общего вида для ( f₁^*, f₂^*) представляется алгебраически сложной задачей (но решения для конкретных случаев легко найти численно), вот почему мы выбрали для рассмотрения Пример 6.2. Даже при сведении задачи к специальному случаю m₁=m₂=m и использование симметрии для снижения проблемы нахождения f ^* = f₁^* = f₂^*, общее решение все ещё затруднено. Но рассматривая вариант, когда a=0 и, следовательно, Cor(U₁,U₂)=-1, получаем g(f) = ln(1+2mf), которая растет без ограничений при увеличении f. Эта пара ставок – “бесспорный факт” и в этом случае следует ставить как можно больше.

Это упрощенная версия классического арбитража на рынке ЦБ: найти пару ценных бумаг, которые идентичны или “эквивалентны” и торговать по расходящимся ценам. Покупая относительно недооцененый инструмент, и вставая в позицию шорт по относительно переоцененному инструменту, и достигая значения корреляции –1, фиксируем безрисковую прибыль. Пример подобного действия произошёл в 1983 году. Инвестиционное партнерство под моим управлением купило “старых” акций АТ & Т на сумму $330 миллионов и продало в шорт выпущенных в то время “новых” акций компании АТ & Т с присоединенными к ней региональными телефонными компаниями “семи сестер”. Большая часть этого объема было проведено за одну торговую операцию, в результате чего это стало тогда крупнейшей в стоимостном выражении сделкой за всю историю NYSE (Нью-Йоркская фондовая биржа, 1 декабря 1983).

Применяя критерий Кэлли к рынку ЦБ мы столкнулись с новыми аналитическими задачами. По ставке в бумагу обычно можно получить много различных результатов, в отличие нескольких вариантов во многих играх. Это приводит к использованию непрерывной, а не дискретной функции распределения вероятностей. Нам нужно найти такое f, которое максимизирует g(f) = Eln(1+fX)= ∫ ln(1+fX)dP(x), где P(x) – вероятностная мера описывающая ожидаемый доход. Часто возникает проблема нахождения оптимального портфеля среди n бумаг, где n может быть «большим» числом. В этом случае x и f - n-мерные вектора, а fx – их скалярное произведение. У нас также есть ограничения – требование 1+fx>0 для того, чтобы ln(.) был определен, и условие ∑ f_i =1 (или некоторые c>0) для нормализации к единице (или к c>0) инвестиций. Проблема максимизации может быть решена в общем виде, так как g(f) – вогнутая функция. Могут быть и другие ограничения, такие как требование f_i ³ 0 для некоторых или всех i (отсутствие коротких продаж), или требования f_i £ M_i либо f_i ³ m_i (пределы объёмов инвестирования в i-ую бумагу), или же условие ∑½ f_i ½ £ M (ограничивает общий размер кредитного рычага, чтобы это удовлетворяло маржинальным ограничениям или требованиям управления капитала). Заметим, что в некоторых случаях недостаточно наличия «хороших» ставок или инвестиций, чтобы применять стратегию с использованием полного f^* , что вынуждает игрока делать уменьшенные ставки, уменьшая в некоторой степени общий уровень роста и риска. Это больше проблема мира азартных игр, чем значительных рынков ЦБ. Дополнительная информация по этим проблемам и техникам может быть найдена в литературе.

(а) Непрерывная аппроксимация.

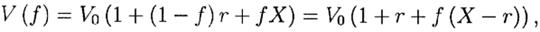Это один из методов, который быстро приводит к примечательным результатам. Пусть X – случайная переменная с вероятностями P(X=m+s)=P(X=m-s)=0,5. Тогда E(X)=m, Var(X)=s². При начальном капитале V₀ , оптимальной доли по ставке f и доходом на единицу X результатом будет

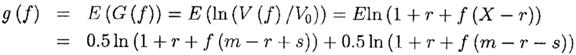где r – ставка дохода на неиспользованный капитал, инвестированный, скажем, в казначейские векселя. Тогда

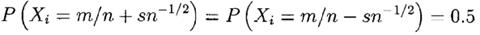Теперь, разделяя временной интервал на n равных независимых шагов, сохраняя то же смещение и ту же общую дисперсию. Таким образом, m, s² и r заменяются на m/n, s²/n и r/n соответственно. У нас есть n независимых X_i , i=1,..,n с вероятностями

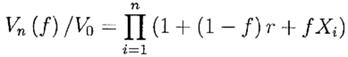Тогда

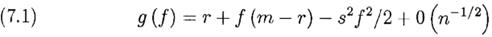Преобразование обоих частей к виду E(log(×)) даёт g(f). Разложение результата в степенной ряд приводит к

где 0(n ^-1/2 ) имеет свойство ограниченности числом n^1/2 (n ^-1/2 ) при n® ∞. устремляя n® ∞ в (7.1) имеем

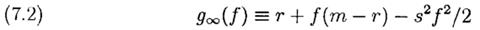
Предел V≡V_∞( f ) функции V_n( f ) при n® ∞ соответствует логнормально распределенному процессу, который является хорошо известной моделью цен ценных бумаг. «Ценная бумага» здесь имеет мгновенную смещение m, дисперсию s², также безрисковые инвестиции с «наличным» денежными доходами по мгновенной ставке r.

Тогда g_∞( f ) в (7.2) – коэффициент роста капитала (мгновенный)по инвестициям или при использовании системы ставок долей f. Нет ничего особенного в нашем выборе случайной переменной X. Любая ограниченная случайная переменная с матожиданием E(X) = m и дисперсией Var(X) = s² приведет к тому же результату. Заметим, что на f больше не накладывается ограничение «быть меньше или равно 1». Обычная проблема неопределенности log(×) для отрицательных аргументов пропала. При f<0 также не возникает затруднений. Это просто соответствует короткой продаже бумаги. Если m < r, то это будет полезно. Отметим также, что инвестор следующий стратегии оптимального f должен теперь регулировать его инвестиции «мгновенно». На практике это означает изменения крошечными приращениями всякий раз, когда появляется небольшое изменение V. Эта идеализация появилась в теории ценообразования опционов. Она широко известна и не мешает практическому применению теории (Black and Scholes, 1973). Наша предыдущая функция роста для ставок с фиксированным шагом была близка к параболической в окрестности f ^*, и часто в диапазоне 0≤ f ≤ 2 f ^*, где также нередко 2 f ^* = f_c. Теперь при использовании ограниченного случая (7.2), g_∞( f ) является точной параболой, лёгкой для изучения.

Логнормальность V( f )/V₀ означает, что log(V( f )/V₀) – нормально распределена, N(M,S²), с матожиданием M = g_∞( f )t и дисперсией S² = Var(G_∞( f ))t для любых t. Из этого мы можем определить, например, ожидаемый рост капитала и время t_k , необходимое для того, чтобы V( f ) стала по крайней мере на k стандартных отклонений больше V₀.

Во первых, с помощью предыдущих методов мы можем показать, что Var(G_∞( f ))= s² f ², отсюда Sdev(G_∞( f ))=s f. Решение t_kg_∞ = kt^1/2Sdev(G_∞( f )) даёт t_kg²_∞ , следовательно ожидаемый рост капитала t_kg_∞, откуда мы ищем t_k. Результаты представлены в уравнениях (7.3).

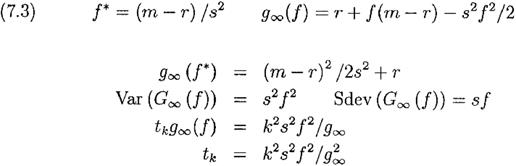
Изучение выражений для t_kg_∞(f) и t_k показывает, что каждое из них увеличивается при увеличении f для 0≤ f ≤ f₊ , где f₊ - положительный корень уравнения s² f ²/2 – (m-r)f – r =0 и f₊>2f ^*.

Комментарий: Модель оценки доходности финансовых активов (САРМ) утверждает, что рыночный портфель лежит на эффективной границе Марковица E на плоскости (s,m) в единственной (как правило) точке P=(s₀, m₀), такой, что линия проведенная через P и точку (s=0, m=r) является касательной к E (в точке P). Наклон этой прямой – коэффициент Шарпа S = (m₀-r₀)/s₀ , а из (7.3) g_∞(f ^*)= S²/2+r, таким образом максимальный уровень роста g_∞(f ^*) для фиксированной r зависит только от коэффициента Шарпа (см. Quaife (1995)). Из (7.3) снова получаем f ^*=1, когда m=r+s², и в этом случае инвестор, использующий критерий Кэлли, будет выбирать рыночный портфель сформированный без заимствований и кредитования. Если m>r+s² инвестор будет использовать кредитный рычаг, а если m<r+s² , то он будет инвестировать часть средств в казначейские векселя и часть в рыночный портфель. То есть инвестор будет динамически перераспределять средства каждый раз при изменении f ^* из-за колебаний и в прогнозе величин m, r и s² ицен бумаг, находящихся в составе портфеля.

Из (7.3) получаем g_∞(1)=m- s²/2, следовательно, все портфели на плоскости (s,m), удовлетворяющие условию m- s²/2=С, где С- константа, имеют одинаковый уровень роста. При использовании непрерывной аппроксимации функцией полезности для Кэлли-инвестора выступает U(s,m)=m-s²/2. Таким образом, для любого (закрытого, ограниченного) набора портфелей лучшими из этого подмножества являются те, которые максимизируют одно параметрическое семейство m- s²/2=С. Смотрите Kritzman in Bernstein and Damodaran editors (1998), Chapter 2 для элементарного введения по связанными с этими идеями.

Пример 7.1. Пересмотр портфеля в долгосрочном периоде. Возьмём r=0 для этого примера. Тогда основные уравнения (7.3) упрощаются до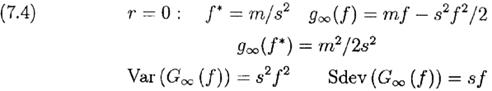

Сколько времени может занять достижение V( f ^*)≥V₀ с определенной вероятностью? Что насчет V( f ^*/2)? Чтобы найти время t необходимое для того, чтобы V( f )≥V₀ с уровнем значимости в k стандартных отклонений (k=1, P=84%; k=2, P=98% и т.д.)мы решаем для t ≡ t_k:

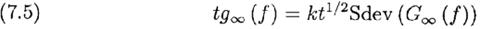
Мы получим лучшее понимание, если нормализуем все f к f ^*. Переобозначая везде f= с f ^* мы находим для r = 0

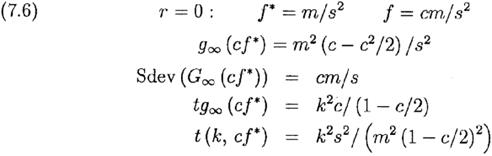
Уравнения (7.6) содержат интересный результат:условие V( f )≥V₀ с уровнем значимости в k стандартных отклонений происходит, когда ожидаемый рост капитала равен tg_∞=k²c/(1-c/2), и этот результат не зависит от m и s.Для f= f ^* (c=1 в (7.6)) это справедливо при k=1 и tg_∞=2, которымсоответствует V=V₀e², а также при k=2 и tg_∞=8 соответствующие V=V₀e⁸. Тогда e⁸=2981 , и при 10%-ой ставке ежегодного (мгновенного) роста потребуется 80 лет для того, чтобы с 98% -ой вероятностью выполнилось V ≥ V₀.

При 20% ставке ежегодного мгновенного роста это займет 40 лет. Однако, при f=f^*/2 значениями для k=1 и 2 будут tg_∞=2/3 и 8/3 соответственно, просто 1/3 от предыдущих. Таким образом, времена ожидания того, что значение Prob(V ≥ V₀) превысит 84% и 98% становятся 6,7 и 26,7 лет соответственно, а ожидаемый коэффициенте роста снизился в ¾ раза по сравнению с уровнем для f ^*.

Комментарий: Использование дробного критерия Кэлли против обычного в случае r=0.

Из уравнений (7.6) мы видим, что g_∞(cf ^*)/ g_∞(f ^*)=c(2-c), 0£ c<∞, показывающее, как коэффициент роста связан с максимальными изменениями c. Относительный риск Sdev(G_∞(cf ^*))/ Sdev(G_∞(f ^*))=c и относительное время для достижения равного ожидаемого общего роста равно 1/c(2-c), 0<c<2. Таким образом, относительный «спрэд» для одинакового ожидаемого общего роста равен 1/(2-c), 0 < c<2. Следовательно, даже выбирая c очень малым, спрэд около данного ожидаемого роста не может быть уменьшен с коэффициентом ½. Соответствующие результаты не настолько просты, как в случае, когда r>0.

(б) Реальный (почти) мир.

Полагаем, что цены изменяются «непрерывно» (отсутствуют «скачки»), что портфели могут пересматриваться «непрерывно», и что отсутствуют транзакционные издержки (рыночные потрясения, комиссии, «накладные расходы») и налоги (федеральные, муниципальные и т.п.). Тогда применима наша предыдущая модель.

Пример 7.2. Возьмем индекс S&P 500. Используя исторические данные мы делаем грубые оценки: m=0,11 ; s=0,15 ; r=0,06. Требующиеся нам уравнения для случая r¹0, являются обобщением (7.6) при r¹0 и f=с f ^*, которые следуют из (7.3):

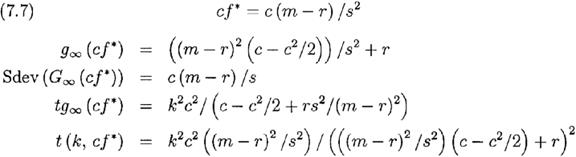
Если мы примем 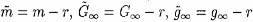, тогда замена переменных в уравнениях (7.7) дают уравнения (7.6), демонстрируя связь между двумя наборами уравнений. Это также показывает, что пример и выводы о P(V_n>V₀) в случае r= 0 эквивалентны аналогичным заключениям о P(ln(V(t)/V₀>rt) в случае r¹0. Следовательно, мы можем сравнивать различные стратегии с вариантами инвестирования, основанных на начислении сложных процентов и безрисковой ставке r, такими как вложения в безкупонные U. S. Treasury Bonds.

Из уравнений (7.7) для с=1 мы находим

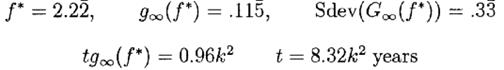
То есть при f ^*=2,22 по истечение 8,32 лет вероятность того, что V_n>V и ожидаемое значение log(V_n/V₀)=0,96 составит 84%, а медианное значение V_n/V₀ будет равно примерно e^0,96=2,61.

Для обычного безрычагового варианта при f=1 и с=0,45 мы получаем

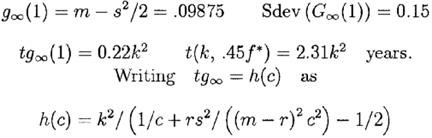
Мы видим, что h(c) растет с увеличением с, по крайней мере до точки с=2, соответствующей 2f ^*.

Запись t(k, cf ^*) =t(c) в виде

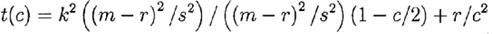
показывает, что t(c) такжерастет с увеличением с по крайней мере до точки с=2.

Таким образом, для меньшего (более консервативный подход) значения f= сf ^* , с£ 2, заданные уровни вероятности P(V_n>V₀) достигаются раньше. При с<1 это сопровождается уменьшением коэффициента роста, относительно небольшим для значений f близкихк f ^*.

Замечание: За период 1975-1997 годов совокупная ежегодная доходность краткосрочных казначейских векселей (значение которой соответствует ставке r, если инвестор производит ссудные операции, то есть f<1) изменялась от низкой 2,90%(1993) до высокой 14,71% (1981). Для получения детальной информации см. ежегодный сборник Ibbotson Associates 1998 (или последний доступный) Yearbook.

Крупный инвестор с хорошими связями мог бы заимствовать у брокера при запросе плюс около 1%, что приблизительно соответствовало бы казначейским векселям плюс 1%.

Это могло бы быть целесообразной оценкой для инвестора, который делает заимствования (f>1). Для других ставки вероятно будут выше. К примеру, базисная ставка за 1975-1997 гг. менялась от низкой 6% (1993) до высокой 19% (1981), по данным Associates First Capital Corporation (1998).

Так как r колеблется, мы ожидаем, что m имеет тенденцию к инверсным по отношению к r колебаниям (высокий процентные ставки вызывают снижение цен на фондовых рынках по хорошо известным причинам). В соответствии с этим f ^* и g_∞ будут также колебаться, поэтому в долгосрочном периоде инвестор индексного фонда S&P нуждается в процедуре периодической переоценки и изменения f ^*_, а также желаемого им уровня ливереджа или наличности.

Для иллюстрации влияния условия r_b>r, где r_b – это ставка по заемным средствам инвестора, предположим, что r_b в примере (7.2) имеет значение r+2% или 0,08, этот выбор основан на приведенных выше исторических значениях r, которые являются промежуточными между «хорошим» r_b =r+1% и «плохим» r_b =базисная ставка = r+3%. Мы заменяем r на r_b в уравнениях (7.7),и , f ^*>1; f ^*=1,33; g_∞( f ^*)= 0,100; Sdev(G_∞(f^*))=0,20; tg_∞( f ^*)=0,4k²; t=4k² лет. Заметьте насколько сильно уменьшилось f^*.

Комментарий: Налоги.

Предположим для простоты, что все прибыли облагаются налогом с постоянной ставкой T, а все убытки имеют налоговые льготы (возврат налога) с такой же постоянной ставкой T. Рассматривая сущность этих налогов совместно, представим их как партнера, владеющего частью Т всех прибылей и убытков. Тогда уравнения (7.7) переходят к виду:

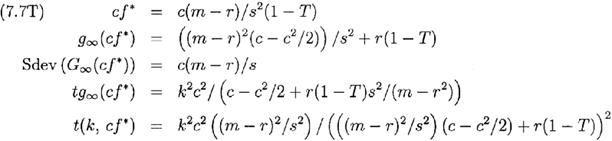
Интересно увидеть, что cf ^* увеличилось на коэффициент 1/(1-Т). Для жителя Калифорнии с большими доходами предельная совокупная ставка федеральных и местных налогов составляет 45%, следовательно коэффициент равен 1/0,55= 1,82. Увеличение cf ^* приводит к тому же самому значению коэффициента роста, что и до ожидаемого изменения из-за влияния rT. Величина Sdev осталась неизменной, а t(k, cf ^*) незначительно увеличилась. Однако, как показывает практика, использование более высокого значения кредитного плеча, необходимого в условиях высокой ставки налога, обычно неприемлемо из-за условий маржинальных операций, или нецелесообразно из-за невозможности непрерывного регулирования, и в реальных условиях создаёт опасности, степень которых быстро растет с ростом коэффициента ливереджа.

(в) Случай для «дробного критерия Кэлли».

На Рисунке 5 показаны три кривые g для реальных значений m: m_t=0,5m_e; 1,0m_e и 1,5m_e , где m_e является оценочной величиной для m. Вертикальные линии и горизонтальные стрелки показывают снижение g в трёх случаях: f =0,5 f_e^*; f_e^* и 1,5f_e^*. Например с f =0,5 f_e^* или «полукэлли» мы не имеем проигрыша и достигаем максимума g=0,25 в случае m_t=0,5m_e. Но если m_t=m_e, тогда g=0,75 c проигрышем 0,25, а если m_t=1,5m_e, тогда g=1,25 c проигрышем 1,0, где для всех g единицами измерения были m_e²/2s². Это отмечено маркерами LOSS₁ и LOSS₂ на вертикальной линии выше f/f_e^*=0,5, а также двумя соответствующими стрелками, направленными вверх, и в данном случае вправо от этой линии. Катастрофа происходит, когда m_t=0,5m_e, и мы выбираем f=1,5f_e^*. Здесь сочетается увеличенные на 50 % по сравнению f_e^* величины ставок и переоцененное значение для m_t=2m_e. Тогда g=-0,75 и мы терпим крах. Но выбор f=f_e^* также не будет хорошим решением, ведь m_t=0,5m_e и g=0 и наблюдаются «дикие» увеличивающиеся колебания вверх и вниз относительно точки нашего начального капитала. Опыт показывает, что во время значительного направленного вниз колебания игрок в большинстве случаев или выходит из игры, или его исключают из-за требования к минимальному размеру ставки.

Некоторые уроки: (1) В некоторой степени m_e является неустойчивой оценкой для m_t, и благоразумно принимать m_t< m_e и выбирать достаточным для предотвращения варианта g£ 0 значение f<f_e^*.

Оценки для m_e в условиях фондового рынка имеют значительную степень недостоверности, и, в частности, вероятнее будут слишком большими, чем слишком маленькими. Цены финансовых инструментов изменяются по законам «нестационарного процесса», где изменения m и s отчасти непредсказуемы с течением времени. Экономическая ситуация может измениться для отдельных компаний, отраслей промышленности, или для всей экономики в целом. Работоспособные системы могут частично или полностью основываться на технологии «data mining», таким образом m_t может быть существенно меньше чем m_e. Изменения в «правилах игры», такие как комиссии, налоговое законодательство, маржинальные условия, законы инсайдерской торговли и т.п. также могут влиять на m_t. Системы, занимающиеся привлечением капитала, который давит на исключительные значения m_t сверху вниз по направлению к средним значениям. Смещение книзу означает, что наиболее вероятно справедливо m_e> m_t.

Подобные предупреждения большей частью действуют и при игре на спортивном тотализаторе, с разницей в деталях. Изменения правил, к примеру, могут включать: добавление дополнительных команд; правило трёхочкового броска в баскетболе; игра в «овертайм» для исключения ничьих; изменение типов бит, мячей, перчаток, ракеток или покрытий.

Блэкджек отличается от рынка ценных бумаг и спортивных тотализаторов тем, что вероятности дохода в общем говоря могут быть или рассчитаны или смоделированы с любой наперед заданной точностью. Но даже здесь m_t вероятно будет по крайней мере слегка меньше чем m_e. Учитывая усталость игрока и его ошибки, вычислительные ошибки и недочёты в применении или теории блэкджека или теории Кэлли (например, вычисляя точное значение f ^*, последствия чего мы обсуждали ранее), эффекты фиксированной позиции тасовки, не случайная тасовка, преимущественная тасовка, шулерство и т.п.

(2) Согласно (1) выбор f в диапазоне 0,5f_e^*£ f< f_e^* обеспечивает защиту от случая g£ 0 с уменьшением g, которое вероятно будет не более 25%.

Пример 7.3. Великий «сложнопроцентщик». В 1964 году молодой управляющий хедж-фонда приобрёл значительную долю в маленькой текстильной компании из Новой Англии под названием Berkshire Hathaway. Её акции торговались тогда по 20. В 1998 они торгуются по 70000, что в 3500 раз больше, а ежегодная ставка роста по сложному проценту составила около 27%, что равно 24%-ой мгновенной ставке. Некогда молодой управляющий хедж-фонда Warren Buffet – по общему признанию сейчас является величайшим инвестором нашего времени и обладателем вторым по величине состояния во всем мире. Вы можете прочитать о нем в (Buffet and Clarck,1997), Hagstrom (1994), Kilpatrick (1994) и Lowenstein (1995). Если бы вы были достаточно удачливы, как был я, чтобы повстречать Баффета и определить возможные перспективы компании Berkshire, какую стратегию предполагает использование нашего метода? Примем (что-то типа меньшего уровня смещений) m=0,20; s=0,15; r=0,6 (примечание: Правдоподобные аргументы в пользу малого значения смещений в будущем включают регрессия по направлению к среднему, увеличение размера компании Berkshire и возникающие риски из-за устаревания методов менеджмента. Контраргумент – сложнопроцентная ставка динамики роста компании в последние годы была также высока, как и раньше. Однако, индекс S&P 500 в последние годы показывает гораздо более высокие результаты, так что разрыв в величинах уровней роста индекса и Berkshire был несколько меньше. Таким образом, если мы ожидаем, что уровень роста индекса будет возвращаться по направлению к историческому среднему значению, тогда мы ожидаем того же самого поведения от Berkshire, даже в ещё большей степени.) Из уравнений (7.3) или (7.7),

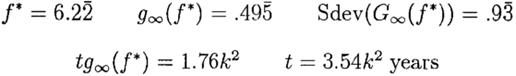
Сравним это с безрычаговым портфелем, где f=1 и с=1/6,2(2)=0,1607.

Мы находим

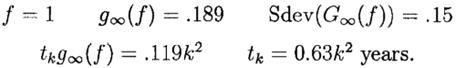
Кредитное плечо здесь на уровне 6,2(2) будет нецелесообразным в реальности из-за того, что цены на бумаги могут меняться внезапно и прерывно. Во время краха в октябре 1987 года индекс S&P 500 упал на 23% за один день. Если это произошло при плече 2,0 , новое значение плеча неожиданно становиться 77/27=2,85 перед перетряской портфеля путём продажи его части. В случае c Berkshire, где был большой хорошо диверсифицированный портфель, предположим, что мы выбираем консервативное значение f=2,0 . Отметим, что это максимально возможное для «клиентов» при нынешних правилах начальное значение плеча. Тогда g_∞(2)=0,295. Медианные значения V_∞/V₀ за 30-ти летний период приблизительно равны: для f=1: V_∞/V₀=288;для f=2: V_∞/V₀=6,974; для f=6,2: V_∞/V₀=2,86х10⁶. То есть разница в результатах при использовании плеча громадна за этот период. (примечание:Art Quaife сообщал о s=0,24 для периода 1980-1997. Читателю предлагается исследовать пример самостоятельно с этим изменением.)

Результаты раздела 3 непосредственно применимы к этой модели непрерывной аппроксимации портфеля ценных бумаг с (возможно) использованием кредитного плеча. Причиной тому – что обе модели подвержены воздействиям одинаковой динамики, а именно logG_n(f) аппроксимированное (шкалированное) Броуновским движением со смещением. Следовательно, мы можем ответить на тот же вопрос, на который мы отвечали при рассмотрении системы ставок в казино в разделе 3, но применительно к нашему портфелю. Например, (3.2) становится

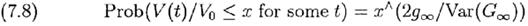
где ^ означает знак возведения в степень, а 0<x<1. Используя (7.4), для r=0 и f=f ^* ; 2g_∞/Var(G_∞)=1, и это упрощается до

Сравним с Примером 3.3. При 0<r<m и f=f ^* показатель степени х в (7.9) становится 1+2rs²/(m-r)² , а также имеет положительную первую производную, следовательно P(·) уменьшается с увеличением r (так как 0<x<1, стремится к 0 при стремлении r к m, что мы и ожидали).

(d) Примечательная формула.

В ранних редакциях этой статьи показатель степени в уравнениях (3.2), (7.8) и (7.9) был без множителя 2, который я непреднамеренно пропустил при анализе. Впоследствии, 19 июня 1997 года Don Schlesinger опубликовал в интернете на сайте www.bjmath.comещё две формулы общей непрерывной аппроксимации для случая r=0.

Если V₀ – начальный инвестиции и y>1>x>0, тогда для f ^* вероятность того, что V(t) достигнет yV₀ быстрее xV₀ будет

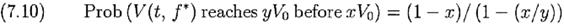
а с большей степенью общности, для f =сf ^*, 0<с<2

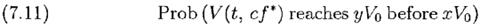
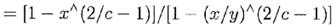
где ^ означает знак возведения в степень.

Очевидно, что (7.10) следует из (7.11) при выборе с=1. Случай r=0 для нашего уравнения (7.8) следует из (7.11), а тот же случай для уравнения (7.9) следует из (7.10). Мы можем получить обобщение (7.11) используя классическую формулу краха игрока (Cox and Miller, pp.205-6), где мы рассматриваем log(V(t, f)/V₀) как реализацию диффузного процесса со средним g_∞, дисперсией v(G_∞), начальным значением 0 и абсорбционными границами log y и log x. Результат будет

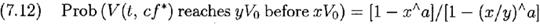
где a=2g_∞/ V(G_∞)= 2M/V, M и V – сдвиг и дисперсия соответственно диффузного процесса на единицу времени. С другой стороны (7. 12) представляет собой иную запись известного решения для Винеровского процесса с двумя границами сдвига (Cox and Miller, Example 5.5).

Как отмечал Shlesinger, выбор x=1/2 и y=2 в (7.10) даёт Prob(V(t, f ^*) doubles before halving)=2/3. Рассмотрим теперь игрока или инвестора, который концентрирует внимание только на значениях V_n= 2ⁿ V₀, n=0, ±1, ±2,… кратное изменение его начального капитала.

В логарифмическом пространстве log(V_n/V₀)=n log2, то есть мы имеем случайное блуждание целыми множителями log2, где вероятность увеличения р=2/3 , а уменьшения q=1/3. Это дает нам удобное наглядное и компактное представления уровня риска стратегии Кэлли.

Если же мы выберем с=1/2 («полукэлли»), уравнение (7.11) дает Prob(V(t, f ^*) doubles before halving)=8/9, что приводит к коэффициенту роста g_∞(f ^*/2)=0,75g_∞(f ^*), таким образом «полукэлли» имеет коэффициент роста равный 3/4f ^*, но гораздо меньший шанс потерпеть большие убытки.

Второе полезное наглядное сравнение риска вытекает из уравнения (7.8), которое даёт

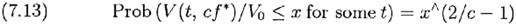
Для с=1 мы имеем Prob(×)=x, а для с=1/2 мы получаем Prob(×)=x³. Следовательно «полукэлли» имеет значительно сниженную вероятность значительных потерь капитала. Шанс потери в какой-либо момент половины начального капитала составляет ½ для f =f ^*, но только 1/8 для f =f ^*/2. Мой опыт игры и инвестирования, так же как и сообщения от многочисленных игроков и команд блек-джека, говорит, что большинство людей почти всегда предпочитают безопасность роста и психологический комфорт «полукэлли» увеличению на четверть коэффициента роста.

8 Исследование конкретного примера

Летом 1997 года корпорация XYZ (псевдоним) получила значительное количество наличных денег. Это отмечено в колонке 8/17/97 листинга изменения структуры их портфеля, представленного в Таблице 8.1. В портфеле было 54% акций Biotime (тикер BTIM), биотехнологической компании, котирующейся на NASDAQ. Это было связано с существующими и историческими связями между людьми из XYZ Corp. и BTIM. Служащие и руководство XYZ были очень хорошо осведомлены о положении дел в BTIM, и это давало им ощущение того, что они были особенно хорошо подготовлены, для того чтобы оценить компанию как объект инвестирования. Они пожелали и дальше держать значительную позицию по BTIM.

Портфель содержал акции Berkshire Hathaway, тикер BRK, впервые купленные в 1991 году.

(а) Ограничения.

Доктор Quaife определил Кэлли-оптимальный портфель для XYZ Corp. исходя из конкретных ограничений. Список потенциально возможных бумаг был ограничен следующим составом:BTIM, BRK, бумаги индексного фонда Vanguard 500 (S&P 500), казначейские векселя. Позиция шорт по казначейским векселям была использована в качестве демпфера на случай маржинальных долгов. Брокер XYZ кредитовал компанию по ставке на 2% дороже, чем было учтено в анализе. Простая САРМ модель предполагает, что инвестор рассматривает рыночный портфель (здесь замененный на индекс S&P 500 по хорошо известным причинам), а также использует заемные средства и кредитование. Как Quaife, так и автор убеждены, что BRK была и является превосходной альтернативой, а их знания о компании и долгий опыт работы с BRK подтверждают это.

Действия XYZ Corp. была подчинены маржинальным требованиям: 50% сначала и 30% далее, означающие, что портфель ценных бумаг формируется при условии, что первоначальный маржинальный долг (средства, одалживаемые у брокера) ограничен величиной 50% от стоимости бумаг, и что значение величины маржинального долга в дальнейшем не должно превышать 30% от стоимости портфеля, а также ценные бумаги должны продаваться при рассогласовании, чтобы обеспечить соблюдение требования в 30%-ом ограничении.

В дополнение к этому XYZ Corp. желает оставить значительную часть акций BTIM в своём портфеле.

(b) Анализ и результаты

Используя помесячные данные за период 3/31/92 – 6/30/97 (всего 63 месяца) Quaife определил средние, ковариации и т.д. представленные в Таблице 8.1.

Таблица 8.1 Статистики для логарифмов относительных помесячных изменений капитала за период 3/31/92 - 6/30/97.

		Berkshire	BioTime	SP500	T-bills
Месячное среднее		0.0264	0.0186	0.0146	0.0035
Стандартное отклонение		0.0582	0.2237	0.0268	0.0008
Годовое среднее		0.3167	0.2227	0.1753	0.0426
Стандартное отклонение		0.2016	0.7748	0.0929	0.0028
Месячные ковариации	Berkshire	0.0034	-0.0021	0.0005	1.2E-06
	BioTime		0.0500	-0.0001	3.2E-05
	SP500			0.0007	5.7E-06
	T-bills				6.7E-07
Месячные корреляции	Berkshire	1.0000	-0.1581	0.2954	0.0257
	BioTime		1.0000	-0.0237	0.1773
	SP500			1.0000	0.2610
	T-bills				1.0000

Обратим внимание, что среднее у BRK выше, а стандартное отклонение ниже, чем у BTIM, следовательно, мы ожидаем, что эта бумага будет выделена дальнейшим анализом. Но отметим также, что имеется отрицательная корреляция с BTIM, которая предполагает, что добавление в портфель некоторого количества BTIM к уже имеющейся BRK может оказаться выгодным.

Используя статистику из Таблицы 8.1, Quaife определил нижеследующие оптимальные портфели соответствующие разным условиям заимствования.

Таблица 8.2 Составы оптимальных портфелей для различных посылок об условиях заимствования.

Доля ценной бумаги
Наименование	Без заимствования	50% заемных	Неограниченное заимствование
Berkshire	0.63	1.50	6.26
BioTimc	0.37	.50	1.18
S&P 500	0.00	0.00	12.61
T-bills	0.00	-1.00	-19.04
Коэффициент роста портфеля
Среднее	0.36	0.62	2.10
Стандартное отклонение	0.29	0.45	2.03

Как и ожидалось, BRK важнее и предпочтительнее, чем BTIM, но добавление некоторого количества BTIM дает лучший вариант.

Если предполагается использование неограниченного размера заемных средств, то было бы неразумным выбрать соответствующий этому варианту портфель в Таблице 8.2.

Различные положения, лежащие в основе этого анализа являются только лишь аппроксимациями разных степеней точности: цены на фондовом рынке не меняются непрерывно; пересмотр состава портфеля не может быть непрерывным процессом; стоимость транзакций не равна 0; ставка по заемным средствам больше чем доходность казначейских векселей; в анализе должна использоваться величина прибыли после налогообложения; процесс, формируемый потоком доходностей по бумагам не стационарен, и наши точечные статистические оценки в Таблице 8.1 неустойчивы. Мы также отметили раньше, что так как чрезмерные размеры ставок более опасны, чем недостаточные, использование «дробного Келли» представляется предпочтительным, как в большей степени отражающего неопределенности.

Фактически использованные данные относятся к периоду 1982-1997 гг., который был сильнейший бычим рынком за всю историю. Мы могли бы ожидать снижение доходностей к направлению к средним, поэтому средние в Таблице 8.1 вероятно являются переоцененными для ближайшего будущего. Ряды данных неизбежно коротки из-за ограниченности информации по BTIM, что вносит дополнительную неопределенность. Для оценки чувствительности Quaife использовал традиционные (среднее, стандартное отклонение) оценки для относительных изменений цен (не для их логарифмов): у BRK (1,15;0,20), у BTIM (1,15;1,0), а у S&P 500 (1,125;0,204) за период 1926-95 по информации из Ibbotson (1996), а также корреляции из Таблицы 8.1. Результат - доли 1,65; 0,17; 0,18 и –1,00 для BRK, BTIM, S&P 500 и T-bills. Средняя величина коэффициента роста была 0,19 , а стандартное отклонение 0,30.

(с) Рекомендации и результат.

На дату 8/17/97 совету директоров компании XYZ Corp. было рекомендовано формирование портфеля с использованием 50% маржинального кредитования и могло бы быть осуществлено немедленно. Совет директоров выбрал бездействие. На 10/9/97 (ка