Основные типы расчетов на прочность

СОПРОТИВЛЕНИЕ МАТЕРИАЛОВ

Методические указания для самостоятельной

работы студентов

Красноярск 2011

ОГЛАВЛЕНИЕ

Введение……………………………………………………………...……………..4

1. Растяжение-сжатие……………………………………………………………....5

Задача 1. Расчёт статически определимой стержневой системы

при растяжение (сжатии)…………………………………………….…6

Задача 2. Расчёт статически определимого ступенчатого бруса

при растяжение (сжатие)………………………………………………14

Задача 3. Расчёт статически неопределимого ступенчатого бруса

при растяжение (сжатие)…………………………….………………...20

2. Плоский изгиб…………………………………………………………………27

Задача 4. Плоский изгиб балки………………………………………………….28

3. Кручение вала ………………………………………………………………….34

Задача 5. Кручение вала……………………………………………………….…34

Введение

Современная действительность требует ускорения научно-технического прогресса, повышения конкурентоспособности выпускаемой продукции, снижения материалоемкости конструкции, повышения производительности, долговечности, надежности машин. Исключительная роль в обеспечении этого процесса принадлежит инженерам, конструкторам, машиностроителям. Значительная роль в формировании облика инженеров широкого профиля отводится дисциплинам общеинженерного цикла и, в частности, дисциплине «Сопротивление материалов». Создавая новую конструкцию, инженер назначает первоначальные размеры ее элементов, проводя прочностные расчеты методами сопротивления материалов. Дальнейший расчет конструкций, как правило, производится с помощью ЭВМ численными методами с использованием пакетов прикладных программ. Однако для анализа достоверности получаемых результатов используется сравнение с результатами расчетов по упрощенным моделям методами сопротивления материалов.

В решении задачи по ускорению развития агропромышленного комплекса страны важная роль принадлежит науке о прочности материалов и конструкций, назначение которой – повысить качество расчета и проектирования, дать теоретическую основу для разработки новых эффективных материалов и конструкций и тем самым способствовать повышению эффективности качества, надежности и экономичности сооружений конструкций машин и приборов.

Цель курса «Сопротивление материалов» - выработка у студента умения производить расчеты на прочность, жесткость и устойчивость элементов инженерных конструкций, применяемых в агропромышленном комплексе, подготовить его к правильному выбору методов расчета и проектирования, с целью обеспечения надежности, экономичности и снижения материалоемкости этих конструкций.

У студентов, изучающих курс «Сопротивление материалов», наибольшие трудности обычно возникают при решении задач. Настоящее методическое указание призвано облегчить процесс изучения данного курса, а главное помочь овладеть методикой решения задач и получить необходимый навык в их решении.

Методическое указание содержит материал, относящийся к разделам: растяжение-сжатие, плоский поперечный изгиб, кручение вала.

В данное методическое указание включены задания для самостоятельной работы студента (30 вариантов задач на каждую тему) и примеры решения типовых задач.

Номер схемы определяется по сумме двух последних цифр шифра зачётной книжки, а номер варианта – по последней цифре шифра.

Растяжение-сжатие

Осевым растяжением бруса называется вид нагружения, при котором равнодействующая внешних сил прикладывается в центре тяжести поперечного сечения и действует вдоль продольной оси. В этом случае в поперечных сечениях стержня из шести внутренних силовых факторов возникает только один – продольная осевая сила N.

Для определения внутренних усилий используется метод сечений.

Сущность метода заключается в следующем:

1. Рассекают (мысленно) тело на две части плоскостью, перпендикулярной продольной оси тела (поперечным сечением).

2.Отбрасывают правую или левую часть тела. Чтобы оставшаяся часть находилась в равновесии, по плоскости сечения должны действовать внутренние силы.

3.Заменяют действие одной части на другую внутренними силами. Так как отсеченная часть тела находится в равновесии, то для определения внутренних усилий, в общем случае нагружения, составляют шесть уравнений статического равновесия:

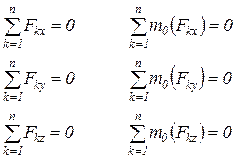
При растяжении в поперечных сечениях стержня возникает только один внутренний силовой фактор - нормальная сила N.

Нормальная сила считается положительной, если она растягивает отсеченную часть стержня, (направлена по внешней нормали), при сжимающем действии нормальная сила считается отрицательной, что можно изобразить графически, как показано на рис.1.1.

Нормальная сила в сечении бруса является равнодействующей нормальных напряжений, действующих в плоскости поперечного сечения

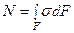
Закон распределения напряжений может быть определен из эксперимента. Установлено, что если на стержень нанести прямоугольную сетку, то после приложения продольной нагрузки вид сетки не изменится, она по-прежнему останется прямоугольной, а все линии прямыми. Поэтому можно сделать вывод о равномерном по сечению распределении продольных деформаций, а на основании закона Гука ( 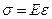) и нормальных напряжений s = const. Тогда N = s F , откуда получим формулу для определения нормальных напряжений в поперечном сечении при растяжении

.

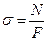Подставляя напряжение в закон Гука получим

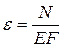
От сюда .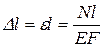

Эта формула выражает закон Гука для абсолютных удлинений. Произведение EF называется жёсткостью поперечного сечения при растяжении и сжатии.

Полное удлинение участка длиной l получим, суммируя удлинения всех бесконечно малых участков.

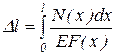
При растяжение (сжатии)

Для статически определимой стержневой системы (см. схемы к задаче 1), загруженной силой Р (см. таблица 1.1) необходимо:

1. Определить продольную силу в каждом из стержней, поддерживающих жёсткий брус.

2. Подобрать размеры поперечного сечения стержней.

Стержень 1 стальной, круглого поперечного сечения. Допускаемое напряжение .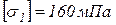

Стержень 2 деревянный, квадратного поперечного сечения. Допускаемое напряжение .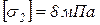

Стержень 3 дюралюминиевый, трубчатого поперечного сечения. Допускаемое напряжение 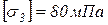. Отношение наружного и внутреннего диаметра составляет 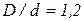. Высоту жёсткого бруса считать малой по сравнению с размерами конструкции и в расчётах её не учитывать.

Схемы к задаче 1

Схемы к задаче 1

Схемы к задаче 1

Схемы к задаче 1

Таблица 1.1

№ варианта	Р, кН	а, м	в, м	с, м	α, град
		0,9		0,3
			1,5	0,6
	12,5	0,9	1,8	0,4
		1,1	1,7	0,5
		1,3	1,6	0,7
	22,3	1,5		0,5
	25,6	1,2	1,7	0,6
	17,8	0,8	1,6	0,2
	11,5	0,7	1,5	0,3
	16,2	1,3	2,1	0,6

Пример решения задачи 1

Для статически определимой стержневой системы (см рис. 1.2), загруженной силой Р необходимо:

1. Определить продольную силу в каждом из стержней, поддерживающих жёсткий брус.

2. Подобрать размеры поперечного сечения стержней.

Рис. 1.2 Схема к примеру решения задачи 1

Стержень 1 стальной, круглого поперечного сечения. Допускаемое напряжение .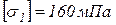

Стержень 2 деревянный, квадратного поперечного сечения. Допускаемое напряжение .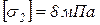

Стержень 3 дюралюминиевый, трубчатого поперечного сечения. Допускаемое напряжение 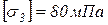. Отношение наружного и внутреннего диаметра составляет .

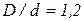Высоту жёсткого бруса считать малой по сравнению с размерами конструкции и в расчётах её не учитывать.

Р=2кН; а=2м; в=2,5; с=0,5м; α=30⁰.

Решение

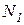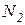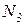Рассмотрим равновесие жёсткого бруса (рис.1.2). Для освобождения бруса от связей мысленно рассечем стержни и заменим связи их реакциями , и . Внутренние усилия, возникающие в стержнях, определим, составив уравнения равновесия.

Из рис.1.2 не трудно заметить, что угол наклона стержня 1 и стержня 3 к оси х одинаков. Обозначим этот угол через α.

Уравнение проекций всех сил на ось х:

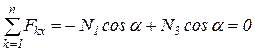. (1.1)

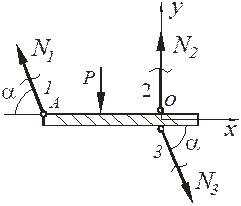
Рис. 1.3 Расчётная схемак примеру решения задачи 1

Уравнение проекций всех сил на ось у:

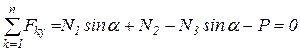. (1.2)

Сумма моментов всех сил относительно точки О:

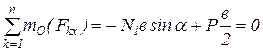. (1.3)

Определим cosα и sinα.

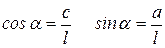
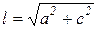
Решая систему трёх уравнений найдём усилия в стержнях.

Из уравнения (1.3) определяем усилие в первом стержне N₁:

.

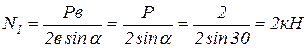Из уравнения (1.1) определяем усилие в третьем стержне N₃:

.

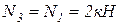Из уравнения (1.2) определяем усилие во втором стержне N₂:

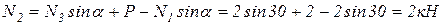
Получили усилия в стержнях одинаковые. Что бы убедиться в правильности наших вычислений сделаем проверку. Составим проверочное уравнения – сумма моментов от всех сил относительно точки А:

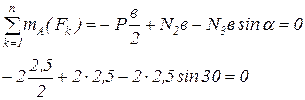
Размеры поперечных сечений определяют из условия прочности при растяжении-сжатии:

.

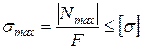Несмотря на то, что усилия в стержнях получились одинаковые, размеры поперечных сечений будут отличаться, так как они выполнены из различных материалов, с разными допускаемыми напряжениями.

1 стержень стальной круглого поперечного сечения. Определим из условия прочности диаметр поперечного сечения стержня:

.

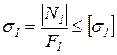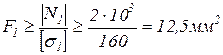
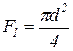
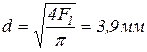
2 стержень деревянный квадратного поперечного сечения. Определим сторону квадрата поперечного сечения:

.

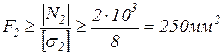
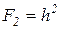
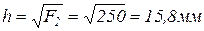3 стержень дюралюминиевый трубчатого поперечного сечения. Определим внешний и внутренний диаметры поперечного сечения:

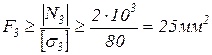
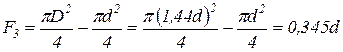
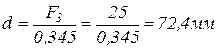D=1,2d=86,9мм

При растяжение (сжатие)

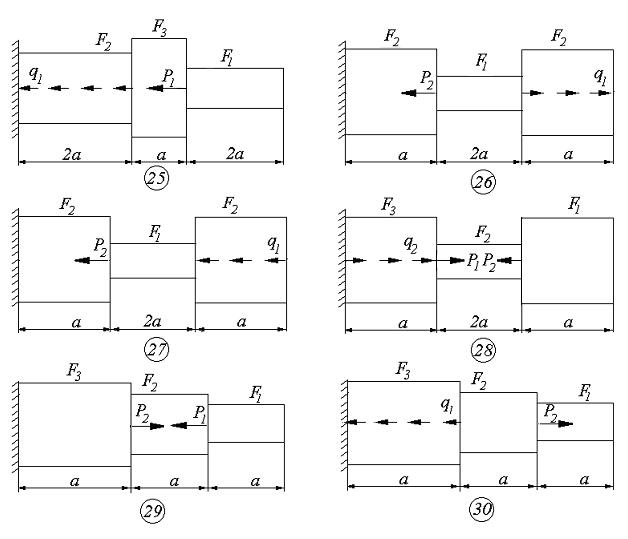
Для статически определимого ступенчатого бруса с жёстко защемлённым концом (см. схемы к задаче 2), нагруженного продольными усилиями Р₁ ,Р₂ , q₁ и q₂ (см. таб. 1.2), необходимо:

1. Построить эпюры продольных сил N, нормальных напряжений s и перемещений .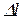

2. Подобрать величину площади поперечных сечений для всех участков бруса из условия прочности по допускаемым нормальным напряжениям при растяжении и сжатии.

Таблица 1.2

№	Р1, кН	Р2, кН	q1, кН/м	q2, кН/м
	10	80	10	70
	20	70	15	80
	30	60	20	90
	40	50	25	60
	50	40	30	50
	60	30	35	40
	70	10	40	30
	80	20	45	20
	10	50	55	50
	20	70	65	20

Принять для всех вариантов следующие соотношения: 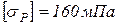, , 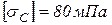Е=10⁵МПа, а=1м.

Схемы к задаче 2

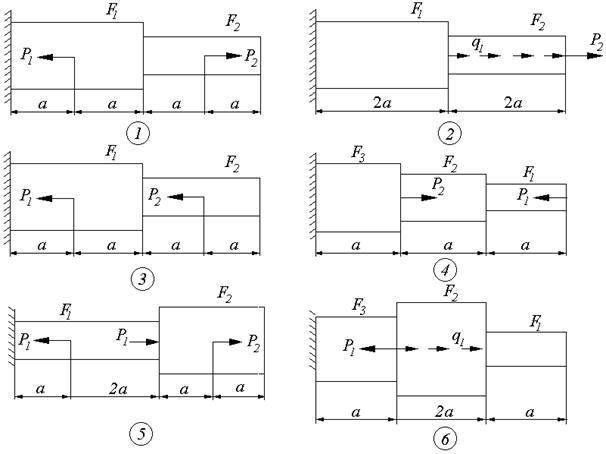
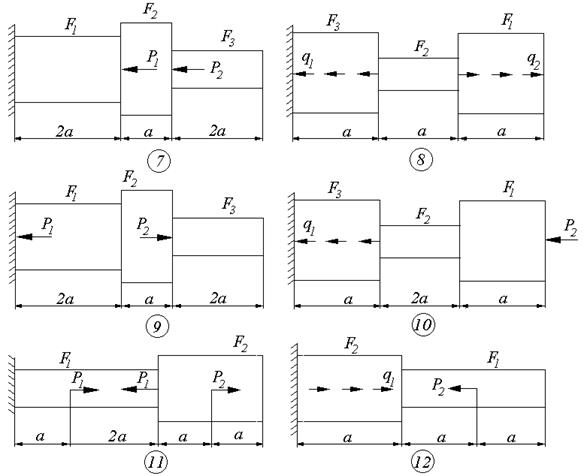
Схемы к задаче 2

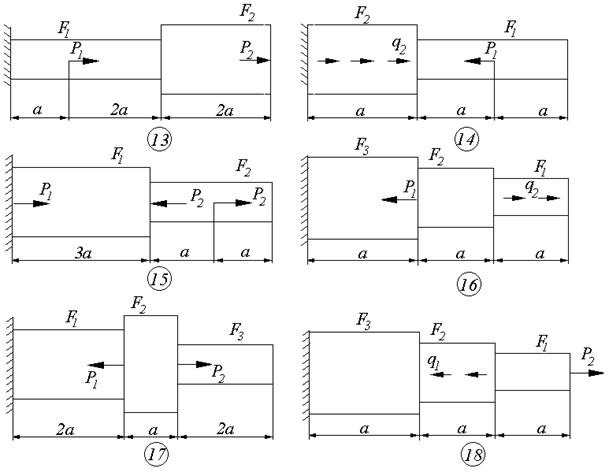
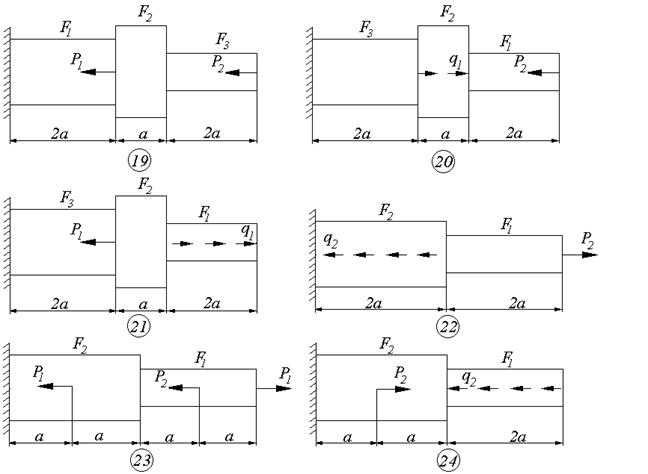
Схемы к задаче 2

Пример решения задачи 2

Для ступенчатого бруса (см. рис.1.4,а) с жёстко защемлённым концом необходимо:

1. Построить эпюры продольных сил N, нормальных напряжений s и перемещений .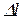

2. Подобрать величину площади поперечных сечений всех участков бруса из условия прочности по нормальным напряжениям, используя следующие числовые значения:

Р₁=30 кН; Р₂=20 кН; q₂=20 кН/м; а=1м; 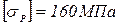; ; 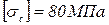Е=1,8×10⁵МПа; F₁=F; F₂=2F; F₃=3F.

Решение

1. Брус состоит из трёх участков. Границами участков являются сечения, к которым приложены внешние силы, или сечения, где изменяются размеры поперечных сечений.

Величину внутренних продольных усилий определим, используя метод сечений. При этом рассматриваем всё время правую отсечённую часть бруса.

Продольную силу N считаем положительной, если нагрузка, её создающая, вызывает растяжение рассматриваемого участка, т.е. направлена от рассматриваемого сечения. Нагрузка, вызывающая сжатие рассматриваемой части бруса, т.е. направленная к сечению, создаёт отрицательную продольную силу. В соответствии с расчётной схемой (рис. 2.1,а) аналитические зависимости для N будут иметь следующий вид:

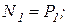
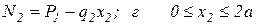тогда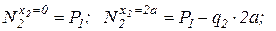

.

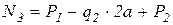После подстановки численных значений, получим:

.

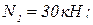
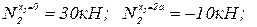
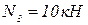На основании полученных значений строим эпюру продольных сил (рис.2.1,б).

Рис. 1.4 Схема нагружения и эпюры N, σ и Δl для ступенчатого

статически определимого бруса

2. Эпюру нормальных напряжений s получим, разделив значения продольной силы N на соответствующие площади поперечных сечений бруса (рис. 1.4,в). Знак продольной силы N определяет и знак соответствующего нормального напряжения s.

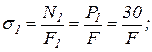
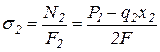, подставляя 2 крайних значения х₂ будем иметь:

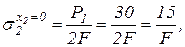
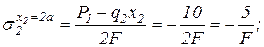
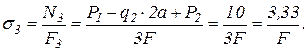
3. Из условия прочности по нормальным наибольшим напряжениям растяжения и сжатия определим параметр F, а затем площади поперечных сечений каждого участка бруса.

Из условия прочности по растягивающим нормальным напряжениям находим:

,

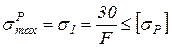отсюда .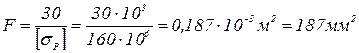

Из условия прочности по сжимающим нормальным напряжениям находим:

,

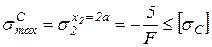отсюда .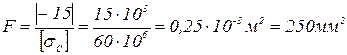

Окончательно выбираем параметр F=250мм².

Определим площади поперечных сечений каждого участка:

F₁=F=250мм², F₂=2F=500мм², F₃=3F=750мм².

3. Зная площади поперечных сечений можно построить эпюру перемещений 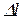(рис.1.4, г). Проще расчёт перемещений вести от заделки, т.е. за точку отсчёта брать сечение, перемещение которого равно 0.

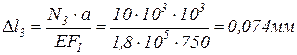
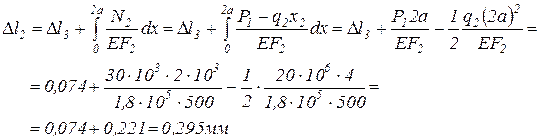
Т.к. уравнение для перемещения на втором участке содержит квадратичную функцию, то графиком функции перемещения на втором участке будет являться парабола, причём в сечении, где 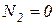парабола будет иметь экстремум. Приравняв уравнение для продольной силы 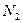к 0, получим расстояние до этого сечения.

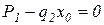
где 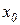- расстояние до сечения, в котором .

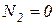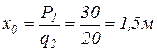
Подставляя, полученное значение для 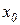, получим значение экстремума на параболе:

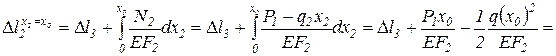
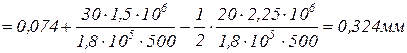
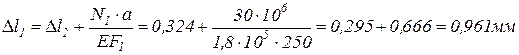
По найденным значениям 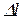строим эпюру перемещений (рис.1.4, г).

При растяжение (сжатие)

Для статически неопределимого бруса с жёстко защемлёнными концами, нагруженного продольной нагрузкой как показано на схеме к задаче 3 необходимо:

1. Построить эпюры продольных сил N, нормальных напряжений 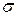и перемещений ;

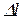2. Подобрать величину площади поперечных сечений всех участков бруса методом допускаемых нагрузок,

Необходимые данные для решения задачи взять из таблицы 1.3.

Схемы к задаче 3

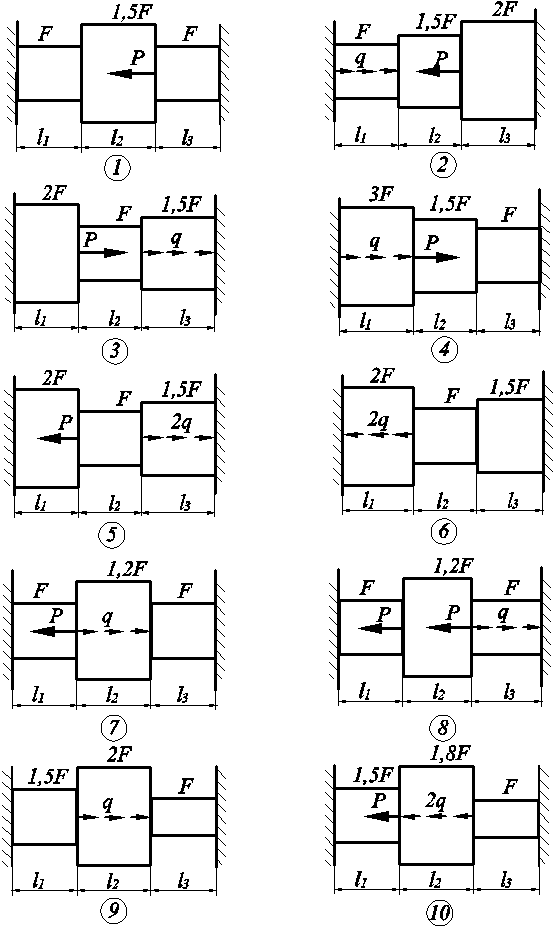
Схемы к задаче 3

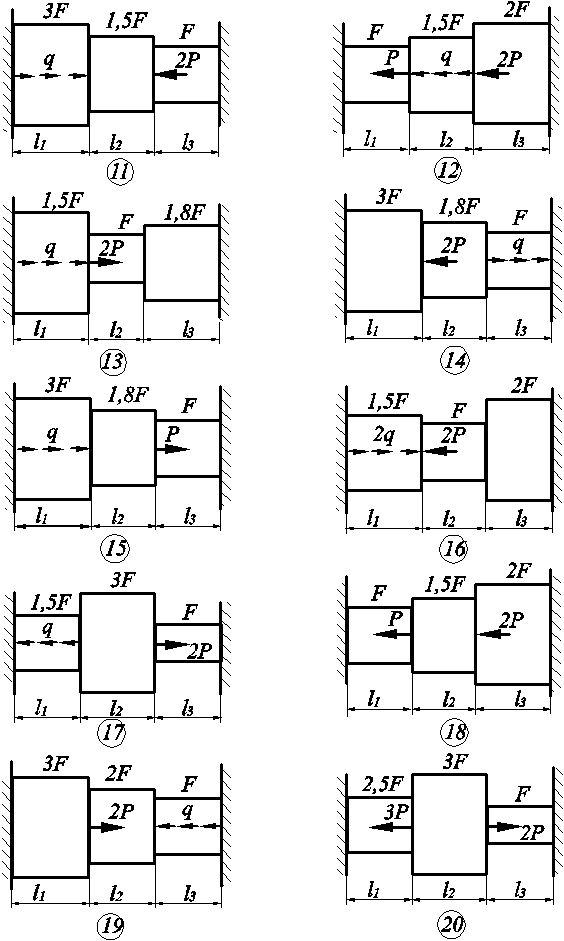
Схемы к задаче 3

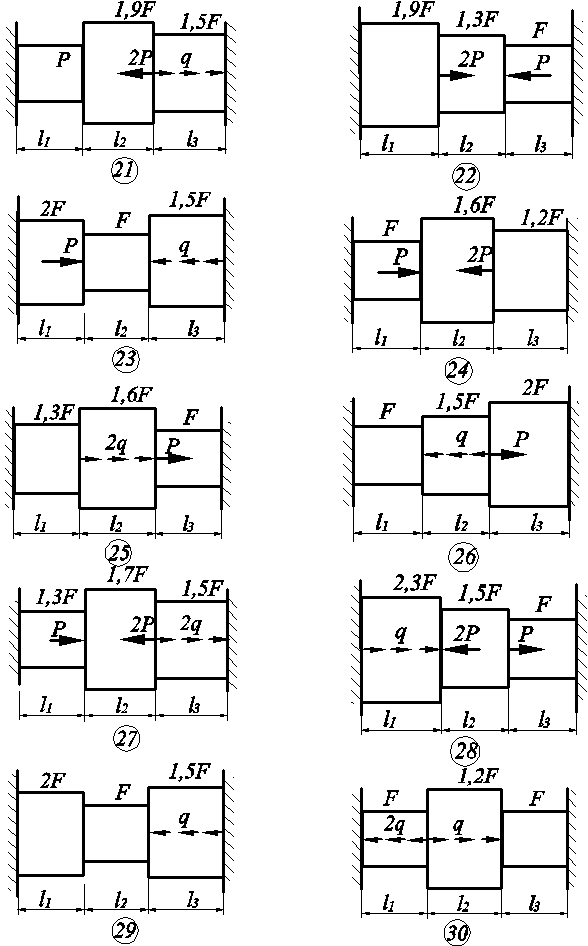
Таблица 1.3

Вариант	Усилия	Длины участков
Р, кН	q,кН/м	l1, м	l2, м	l3, м
	27	12		2	0,5
	35	24	1,2	1,9	0,8
	53	46	1,3	1,8	1
	29	10	1,4	1,7	1,1
	37	22	1,5	1,2	1,2
	45	32	1,6	1,4	2
	10	30	1,7	1	1,8
	15	18	1,8	1,1	1,5
	25	20	1,9	1,2	1,2
	50	44	2	0,8	1

Пример решения задачи 3

Для ступенчатого бруса (см. рис. 1.5а) построить эпюры продольных сил N, нормальных напряжений 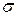и перемещений 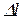; подобрать величину площади поперечных сечений всех участков бруса методом допускаемых нагрузок если Р₁=3Р; Р₂=2Р.

Решение

Задача один раз статически неопределима в силу плоской системы сил, действующих по одной прямой, для которой как известно можно составить только одно уравнение равновесия:

,

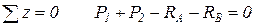в котором два неизвестных: 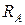и .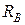

Отбросим правую опору, заменив её действие на брус реакцией .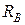

Перемещение сечения в точке В равно нулю, т.к. это сечение жёстко заделано. Используя принцип независимости действия сил, получим уравнение совместности деформаций:

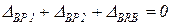
Распишем эти деформации по закону Гука:

,

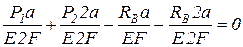отсюда, после сокращения на а и EF, 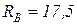кН.

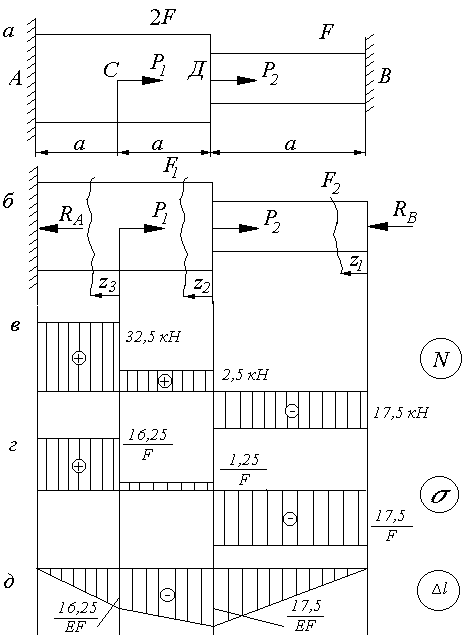
Рис. 1.5 Расчётная схема и эпюры для примера решения задачи 3

В соответствии с расчётной схемой рис. 1.5б аналитические зависимости N, 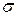и 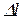будут следующими:

Участок 1

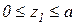
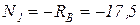кН ; ; .

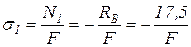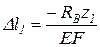Подставим в уравнение для перемещения два крайних значения 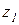, после подстановки будем иметь:

.

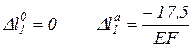Участок 2

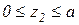
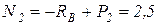кН; ; .

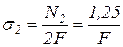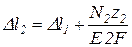Подставляя пределы получим:

.

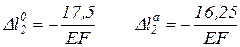Участок 3

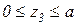
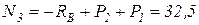кН; ; .

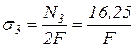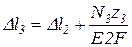Подставляя пределы получим:

.

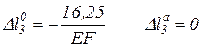На основании данных аналитических зависимостей строим эпюры N, 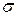и 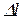(рис. 1.5 в, г,д).

Построение эпюры перемещений может служить проверкой правильности решения задачи. Перемещение на участке 1 при z₁=0 равно нулю, перемещение на участке 3 при z=a также должно равняться нулю, т.к. эти два сечения соответствуют жёсткому закреплению бруса, перемещения которых невозможны.

2. На эпюре нормальных напряжений найдём максимальное напряжение: .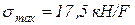

Для определения площади поперечного сечения воспользуемся условием прочности по нормальным напряжениям:

.

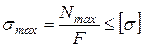Приравняв максимальное нормальное напряжение к допускаемому, определим площадь поперечного сечения F:

.

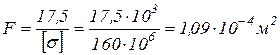Таким образом, на участке 1 площадь поперечного сечения должна быть 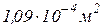, а на участке 2 в два раза больше, т.е. .

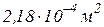Плоский изгиб

Изгиб называется плоским, если плоскость действия изгибающей нагрузки проходит через главную центральную ось инерции сечения.

Если изгибающий момент M_x является единственным внутренним силовым фактором, то такой изгиб называется чистым. При наличии поперечной силы 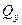изгиб называется поперечным.

Брус, работающий при изгибе, называется балкой.

Построение эпюр поперечной силы Q_y и изгибающего момента M_x является одним из основных этапов при расчете конструкций на изгиб. По эпюрам Q_y и M_x определяется опасное сечение, т.е. сечение в котором может произойти разрушение.

Опасным сечением называется сечение, в котором изгибающий момент достигает наибольшего по модулю значения .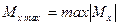

В некоторых случаях опасным сечением может быть также сечение, где наибольшего значения достигает поперечная сила .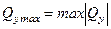

Между поперечной силой и изгибающим моментом существует следующая зависимость:

,

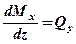то есть первая производная от изгибающего момента по длине участка равна поперечной силе.

Это соотношение в общем виде было получено Журавским и носит название теоремы Журавского.

На основании теоремы Журавского могу быть сформулированы правила проверки эпюр:

1. В точке приложения сосредоточенной силы на эпюре Q_y должен быть скачок, равный по величине и знаку приложенной силе.

2. В точке приложения сосредоточенного момента на эпюре M_x должен быть скачок, равный по величине и по знаку приложенному моменту.

3. На участке, где приложена распределенная нагрузка, эпюра Q_y является наклонной прямой (наклон по направлению действия нагрузки), а эпюра M_x - параболой, выпуклость которой направлена навстречу распределенной нагрузке.

4. На участках, где Q_y > 0, M_x возрастает, на участках, где Q_y< 0, M_x убывает, если Q_y = 0 (эпюра пересекает нулевую линию), то эпюра М_x имеет экстремум.

5. В тех точках, где на эпюре Q_y имеется скачок, на эпюре М_x будет излом.

6. Чем больше по модулю величина Q_{y ,} тем круче изменяется эпюра М_x.

7. На свободных концах балки изгибающий момент равен нулю.

Максимальное нормальное напряжение в балке возникает в сечении, где изгибающий момент достигает наибольшей по модулю величины, то есть в опасном сечении

.

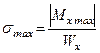Условие прочности при изгибе формулируется следующим образом: Балка будет прочной, если максимальные нормальные напряжения не превысят допускаемых напряжений

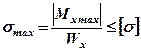
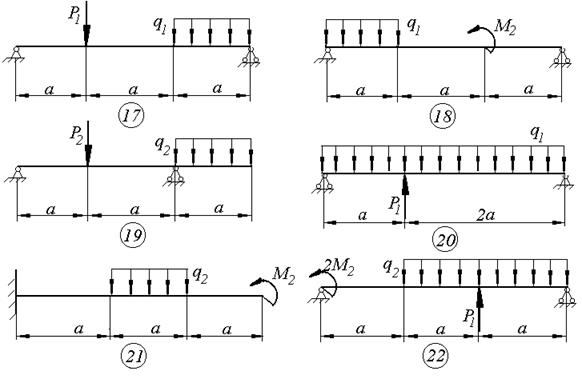
Схемы к задаче 4

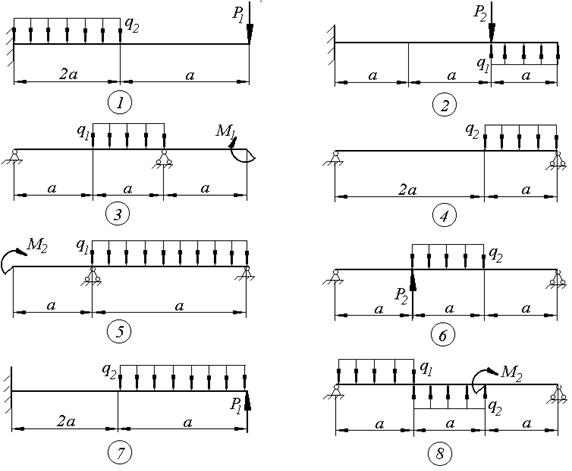
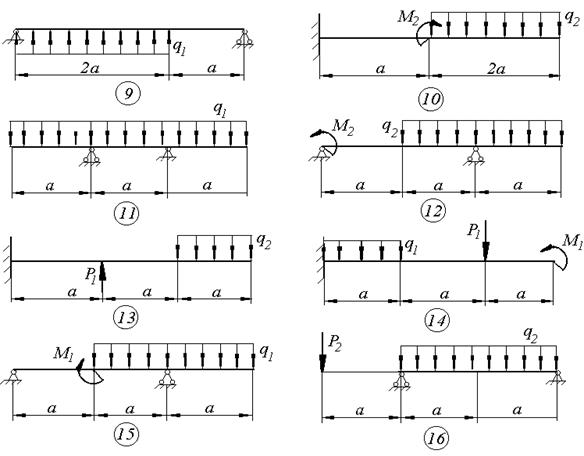
Схемы к задаче 4

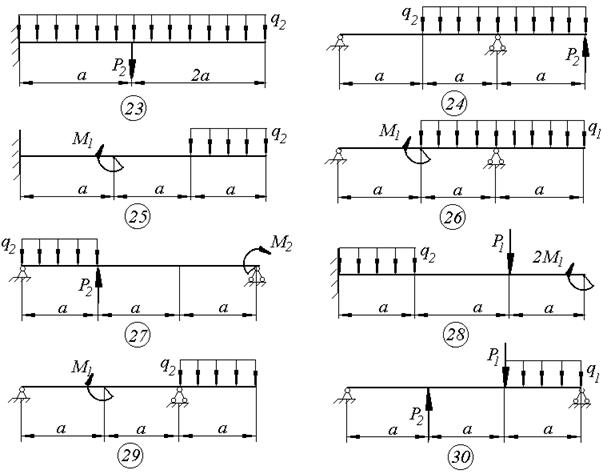
Пример решения задачи 4

Для балки работающей на изгиб (рис. 2.1,а) необходимо:

1. Определить значение поперечной силы Q и изгибающего момента М, построить соответствующие эпюры.

2. Подобрать размеры поперечного сечения балки из условия прочности по допускаемым напряжениям на изгиб для 3-ёх вариантов:

а) двутавра;

б) прямоугольного поперечного сечения со сторонами b и h при соотношении h/b=2;

в) круглого поперечного сечения.

Дано: М=10 кН×м; Р=10 кН; q₁=50кН/м; а=1м; в=1м; с=1м; .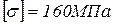

Решение

1. Опорные реакци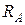и и 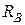(рис. 2.1,б) направим вверх. На балку не действуют горизонтальные силы, поэтому на опоре А будет только вертикальная реакция. Для определения реакций опор составим 2 уравнения равновесия:

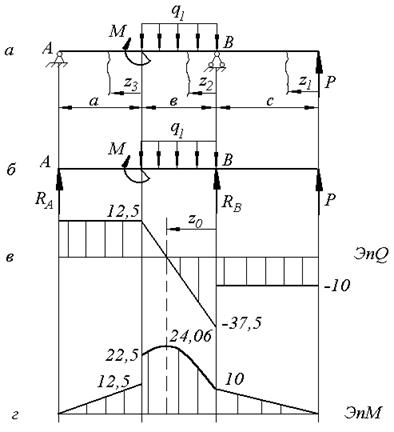
Рис. 2.1 Схема и эпюры внутренних усилий к примеру решения задачи4

;

.

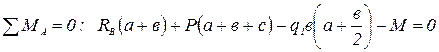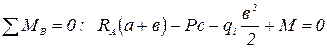Из этих уравнений определим реакци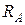и и :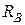

; .

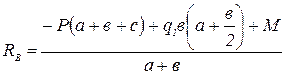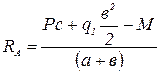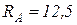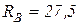После подстановки численных значений получим: кН; кН.

Дополнительное уравнение 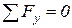можно использовать для проверки полученного результата:

;

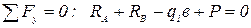12,5+27,5-50+10=0;

2. В поперечных сечениях балки возникают изгибающие моменты М и поперечные силы Q.

При решении задачи используем правило знаков внутренних усилий: поперечная сила Q в сечении положительна, если равнодействующая внешних сил стремится повернуть рассматриваемую часть по часовой стрелке относительно центра тяжести сечения.

Изгибающий момент М в сечении будем считать положительным, если балка изгибается таким образом, что растянутые волокна находятся в нижней части балки, а сжатые – в верней части.

Разобьём балку на 3 силовых участка. Границами участков являются сечения, к которым приложены сосредоточенные моменты и силы, а также конец и начало распределённой нагрузки.

Первый участок: .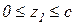

Составим аналитические выражения для определения величины поперечной силы и момента, используя метод сечений и учитывая правило знаков.

;

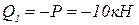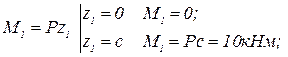
Второй участок: .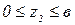

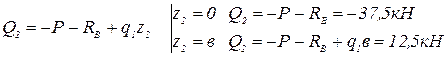
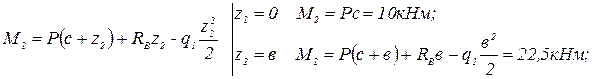
Эпюрой изгибающего момента на 2-ом участке является квадратная парабола (рис.2.1,г). Поэтому для её построения надо знать координаты трёх точек: в начале, в конце участка и в точке, где эпюра имеет экстремум. Экстремум на параболе будет в том же сечении балки, в котором поперечная сила Q равна нулю. Расстояние до сечения, в котором на эпюре момента будет экстремум, обозначим через z₀. Значение z₀ найдём из следующего уравнения:

.

Подставим значение z₀ в уравнение для 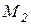и найдём экстремум на параболе.

.

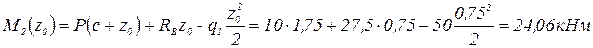Третий участок: .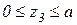

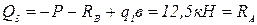
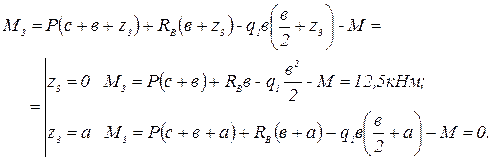
По найденным значениям Q и М строим эпюры поперечной силы (рис.4,в) и изгибающего момента (рис.2.1,г).

3. Из условия прочности балки по нормальным напряжениям подберём размеры поперечного сечения балки для 3-ёх вариантов.

Опасным сечением является сечение балки, проходящее через экстремум на параболе, т.к. в этом сечении будет наибольший изгибающий момент по абсолютной величине 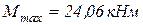. Из условия прочности:

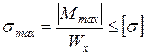
для стальной балки определим :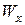

.

а) По найденному значению 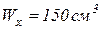подберём номер двутавра по ГОСТ 8239-72. Ближайшая величина момента сопротивления 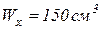, что соответствует двутавру № 18а .

б) Для прямоугольного поперечного сечения момент сопротивления сечения имеет следующую зависимость: , при отношении h/b=2 будем иметь: 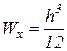, откуда высота сечения 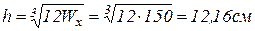, а ширина сечения b=h/2=6,08 см .

в) Для круглого поперечного сечения момент сопротивления сечения следующий: .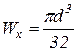

Из этого выражения определим диаметр: .

Кручение вала

Кручением называется вид нагружения, при котором к брусу прикладываются внешние скручивающие моменты, а в поперечных сечениях возникает единственный внутренний силовой фактор - крутящий момент M_к.

Брусья, передающие крутящий момент называются валами.

Зная величины внешних скручивающих моментов и используя метод сечений, мы можем определить крутящие моменты, возникающие в поперечных сечениях вала. В местах приложения внешних моментов ординаты эпюры скачкообразно изменяются на величину приложенного внешнего момента.

Условие прочности при кручении формулируется следующим образом: максимальные касательные напряжения, возникающие в опасном сечении вала, не должны превышать допускаемых напряжений и записывается в виде

.

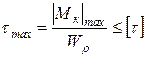Величина 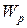называется моментом сопротивления сечения при кручении или полярным моментом сопротивления сечения

Для сплошного круглого сечения

.

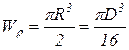Для кольцевого сечения

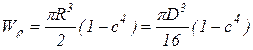, где .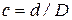

Из условия прочности можно определить диаметр вала:

- для сплошного сечения

,

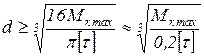- для кольцевого сечения

,

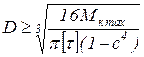Задача 5. Кручение вала

К стальному валу круглого поперечного сечения (см. схемы к задаче 5) приложены сосредоточенный момент М и распределённый момент m необходимо:

1. Составить аналитические выражения для определения внутреннего крутящего;

2. По полученным выражениям построить эпюру крутящего момента;

3. Из условия прочности по касательным напряжениям определить диаметр поперечного сечения;

4. Построить эпюру углов закручивания.

Численные значения приведены в таблице 3.1.

Схемы к задаче 5

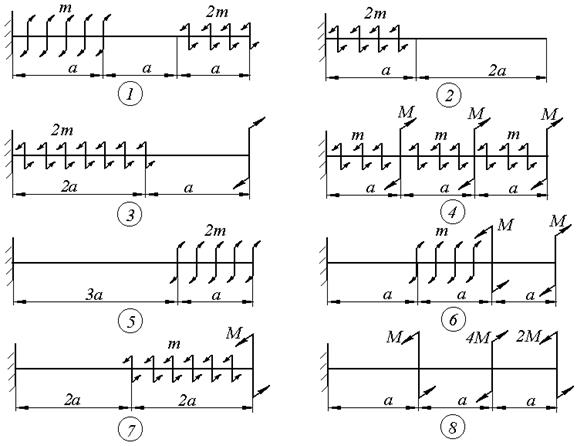
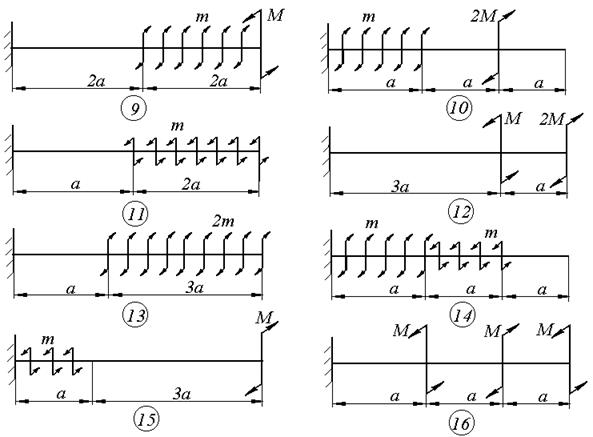
Схемы к задаче 5