Приложения двойного интеграла
1. Площадь плоской области 
вычисляется по формуле:
.
Если область определена неравенствами 
, 
, то
.
Если область определена неравенствами 
, 
, то
.
Если область в полярных координатах определена неравенствами 
, 
, то
.
2. Объем цилиндрического тела, ограниченного сверху непрерывной поверхностью 
, снизу областью на плоскости 
, сбоку цилиндрической поверхностью, параллельной оси Оz, вычисляется по формуле:
.
3. Площадь поверхности 
вычисляется по формуле:
где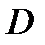 
– проекция данной поверхности на плоскость 
.
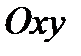4. Масса вещества (пластины), занимающего область плоскости 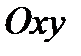и имеющего плотность 
, вычисляется по формуле:
.
При этом статические моментыпластины относительно осей 
и 
вычисляются по формулам:
, 
.
Координаты центра тяжестипластины вычисляются по формулам:
, 
.
В случае однороднойпластины 
координаты центра тяжести вычисляются по формулам:
, 
.
П р и м е р 11. Найти площадь фигуры 
ограниченной линиями:
Р е ш е н и е. Область 
изображена на рис. 23. Она является правильной в направлении оси Ох и удовлетворяет теореме 3.
у у=х+2
2
D
О4 х
-2
Рис. 23
Поэтому получаем:
О т в е т: 
П р и м е р 12.Найти площадь той части конуса 
, которая заключена внутри цилиндра 
.
Р е ш е н и е. Вычислим:
Тогда площадь поверхности вычисляется с помощью двойного интеграла:
,
где областью интегрирования 
является круг с центром в точке (1;0) радиуса 
, ограниченный окружностью 
.
Поэтому получаем:
.
О т в е т: 
.
П р и м е р 13. Найти координаты центра тяжести однородной фигуры, ограниченной линиями 
(рис. 24).
Р е ш е н и е. В данном примере фигура однородна. Поэтому координаты центра тяжести находим по формулам:
где 
- площадь области 
.
у
2
-1 O 2 x
-2
Рис. 24
Учитывая симметрию фигуры относительно оси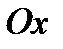 
, вычислим:
;
Следовательно, 
О т в е т: 
.
ПРИМЕРЫ
Вычислить повторный интеграл:
1. 
2. 
Вычислить двойной интеграл по области 
, ограниченной линиями:
3. 
4. 
5. 
6. 
7. 
8. 
Расставить пределы интегрирования в повторном интеграле в одном и
другом порядке, если область ограничена линиями:
9. 
. 10. 
11. 
. 12. 
.
Изменить порядок интегрирования в интегралах:
13. 
14. 
15. 
16. 
17. 
18. 
19. 
20. 
Переходя к полярным координатам, вычислить интеграл, если область 
определена неравенствами:
21. 
22. 
23. 
24. 
25. 
26. 
С помощью двойного интеграла вычислить площадь области,
ограниченной линиями:
27. 
28. 
. 29. 
.
С помощью двойного интеграла вычислить объем тела,
ограниченного поверхностями:
30. 
. 31. 
.
32. 
. 33. 
.
С помощью двойного интеграла вычислить площадь поверхности:
34.Части сферы 
заключенной внутри цилиндра 
.
35. Части плоскости 
, отсеченной плоскостями 
, 
, 
.
36.Найти координаты центра тяжести однородной фигуры, ограниченной линиями: 
.
37.Найти координаты центра тяжести однородной фигуры, ограниченной линиями 
.
ОТВЕТЫ
1. 
. 2. 
3. 
. 4. 
5. 
6. 
. 7. 
8. 
9. 
10. 
11. 
12. 
13. 
14. 
15. 
16. 
17. 
18. 
19. 
20. 
21. 
22. 
23. 
24. 
25. 
. 26. 
27. 
28. 
29. 
30. 
31. 
32. 
33. 
34. 
35. 
. 36. 
. 37. 
.
§ 10. ТРОЙНОЙ ИНТЕГРАЛ