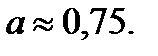Частные и полное приращения функции
Для примера рассмотрим функцию двух переменных 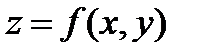 , определенную в некоторой окрестности точки
, определенную в некоторой окрестности точки 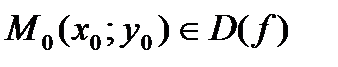 .
.
Пусть 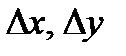 настолько малы, что
настолько малы, что
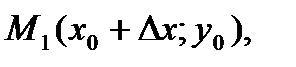
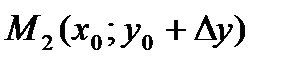 ,
, 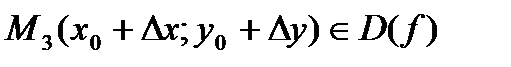 .
.
О п р е д е л е н и е 8.Частным приращением по х функции 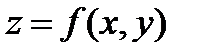 в точке
в точке 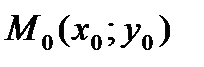 называется выражение:
называется выражение:
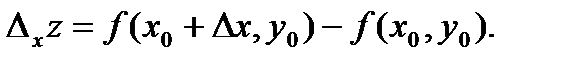
О п р е д е л е н и е 9.Частным приращением по у функции 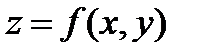 в точке
в точке 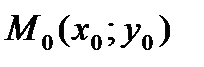 называется выражение:
называется выражение:
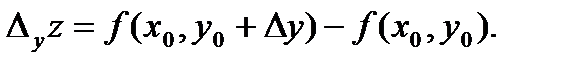
О п р е д е л е н и е 10.Полным приращением функции 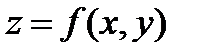 в точке
в точке 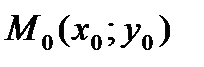 называется выражение:
называется выражение:
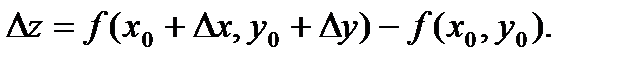
ЧАСТНЫЕ ПРОИЗВОДНЫЕ ФУНКЦИИ
О п р е д е л е н и е 11.Частной производной по х функции 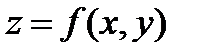 в точке
в точке 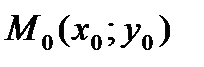 называется конечный предел отношения частного приращения
называется конечный предел отношения частного приращения 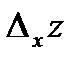 к приращению
к приращению 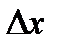 при стремлении
при стремлении 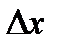 к нулю, если этот предел существует.
к нулю, если этот предел существует.
Используют обозначения: 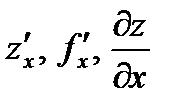 или
или 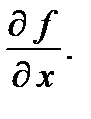
Следовательно, имеем:
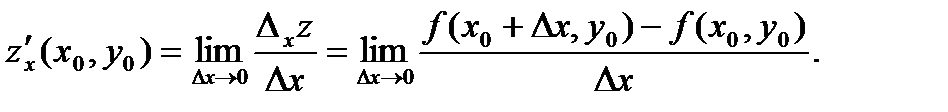
О п р е д е л е н и е 12.Частной производной по у функции 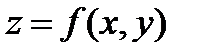 в точке
в точке 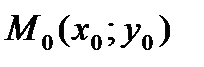 называется конечный предел отношения частного приращения
называется конечный предел отношения частного приращения 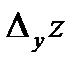 к приращению
к приращению 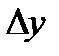 при стремлении
при стремлении 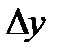 к нулю, если этот предел существует.
к нулю, если этот предел существует.
Используют обозначения: 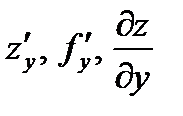 или
или 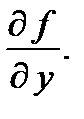
Следовательно, имеем:
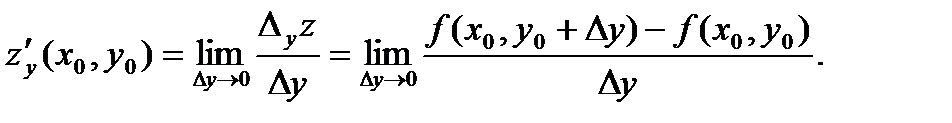
З а м е ч а н и е 2.Из определения частных производных вытекает метод их вычисления: чтобы найти 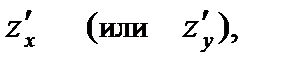 нужно продифференцировать выражение
нужно продифференцировать выражение 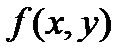 по
по 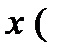 по
по 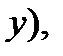 считая величину
считая величину 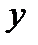 (величину
(величину 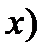 постоянной.
постоянной.
З а м е ч а н и е 3. Понятия частных приращений, полного приращения, частных производных для функции 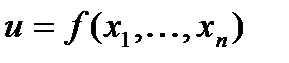 любого числа переменных вводятся аналогично.
любого числа переменных вводятся аналогично.
З а м е ч а н и е 4.Процедура вычисления частных производных функции нескольких переменных сводится к вычислению обыкновенной производной этой функции по одной из переменных при условии, что остальные переменные выступают в роли параметров.
Отсюда следует, что правила вычисления частных производных совпадают с правилами, действующими для функции одной переменной. Однако требуется каждый раз помнить, по какой переменной вычисляется производная, а какие переменные при этом мысленно фиксируются.
П р и м е р 6. Для функции 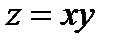 найти частные приращения и полное приращение в точке
найти частные приращения и полное приращение в точке 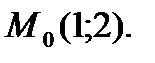
Р е ш е н и е. Воспользовавшись определением, вычисляем в точке 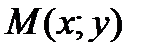 приращения функции
приращения функции 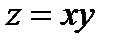 :
: 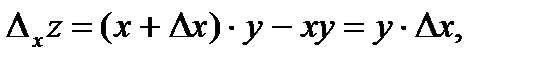
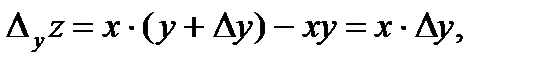
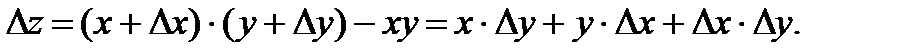
Поэтому в точке 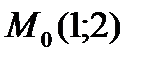 находим:
находим:
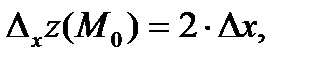
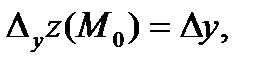
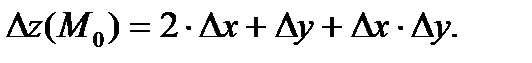
О т в е т: 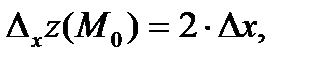
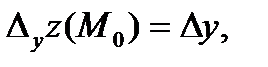
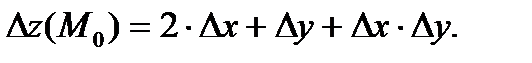
П р и м е р 7. Найти частные производные функции
 (2)
(2)
и вычислить их значения в точке 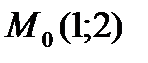 .
.
Р е ш е н и е. Считая в формуле (2) переменную 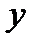 постоянной, находим:
постоянной, находим:
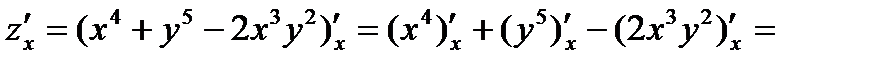
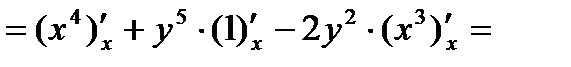
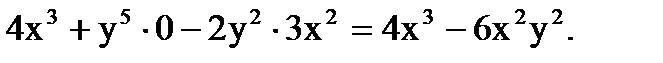
При нахождении 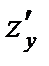 считаем в формуле (2) переменную
считаем в формуле (2) переменную 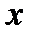 постоянной. Тогда находим:
постоянной. Тогда находим:
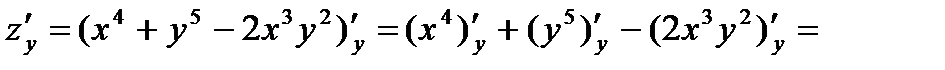
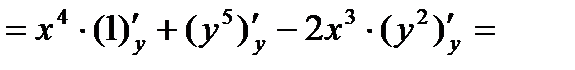
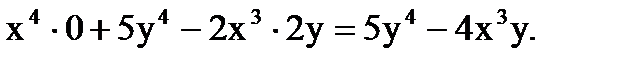
Значения частных производных в точке 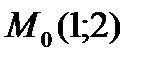 вычислим, подставив в найденные выше формулы
вычислим, подставив в найденные выше формулы 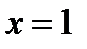 и
и 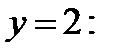
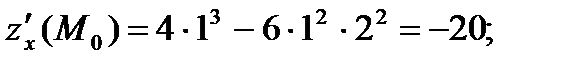
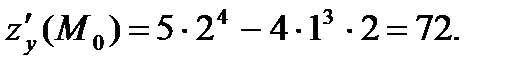
О т в е т: 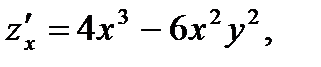
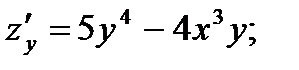

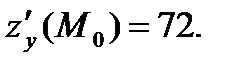
ДИФФЕРЕНЦИРУЕМОСТЬ ФУНКЦИИ
О п р е д е л е н и е 13.Функция 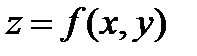 называется дифференцируемой в точке
называется дифференцируемой в точке 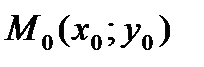 , если в этой точке ее полное приращение представимо в виде:
, если в этой точке ее полное приращение представимо в виде:
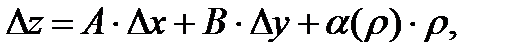 (3)
(3)
где 
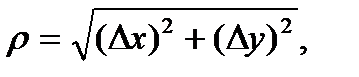
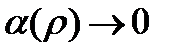 при
при 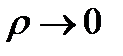 и
и 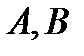 не зависят от
не зависят от 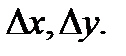
Т е о р е м а 1(о связи дифференцируемости и непрерывности). Если функция 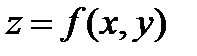 дифференцируема в точке
дифференцируема в точке 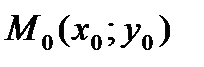 , то она непрерывна в этой точке.
, то она непрерывна в этой точке.
Т е о р е м а 2(о связи дифференцируемости с существованием частных производных). Если функция 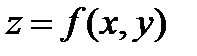 дифференцируема в точке
дифференцируема в точке 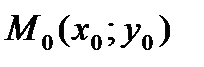 , то в этой точке она имеет частные производные по
, то в этой точке она имеет частные производные по 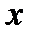 и
и 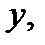 которые равны, соответственно, А и В :
которые равны, соответственно, А и В :
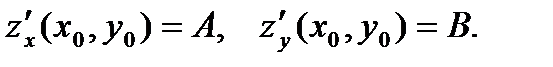
Т е о р е м а 3(достаточное условие дифференцируемости). Если функция 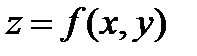 имеет в некоторой окрестности точки
имеет в некоторой окрестности точки 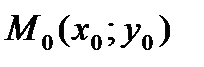 непрерывные частные производные по
непрерывные частные производные по 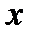 и
и 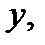 то функция
то функция 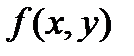 дифференцируема в точке
дифференцируема в точке 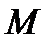 и в формуле (3) имеем:
и в формуле (3) имеем: 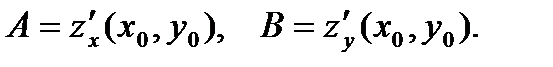
З а м е ч а н и е 5.В случае функции большего (чем два) числа переменных понятие дифференцируемой функции вводится аналогично. При этом естественным образом обобщаются свойства, отмеченные в теоремах 1-3.
О п р е д е л е н и е 14.Функция 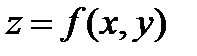 называется дифференцируемой в области
называется дифференцируемой в области 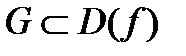 , если она дифференцируема в любой его точке.
, если она дифференцируема в любой его точке.
ПРОИЗВОДНАЯ СЛОЖНОЙ ФУНКЦИИ
Т е о р е м а 4.Пусть функции 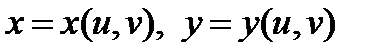 дифференцируемы в некоторой точке
дифференцируемы в некоторой точке 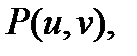 а функция
а функция 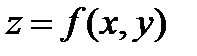 дифференцируема в соответствующей точке
дифференцируема в соответствующей точке 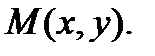 Тогда сложная функция
Тогда сложная функция 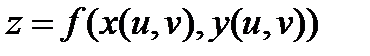 , как функция переменных
, как функция переменных 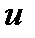 и
и 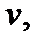 дифференцируема в точке
дифференцируема в точке 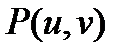 и ее частные производные в этой точке вычисляются по формулам:
и ее частные производные в этой точке вычисляются по формулам:
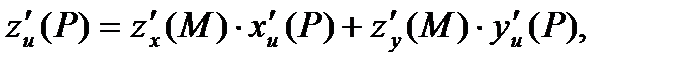
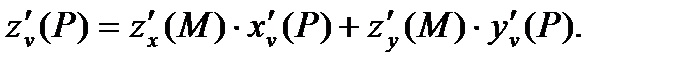 (4)
(4)
З а м е ч а н и е 6. Для случая функций большего (чем два) числа переменных формулы (4) обобщаются естественным образом. Например, если
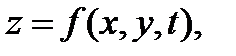
где 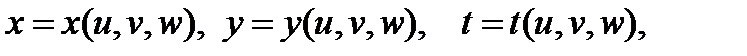 то имеют место аналогичные равенства:
то имеют место аналогичные равенства:
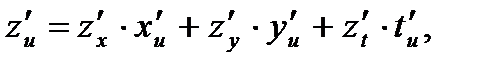
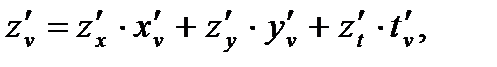
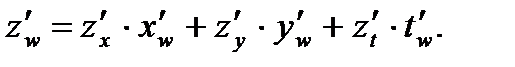
П р и м е р 8. Вычислить 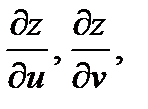 если
если 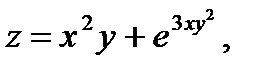 где
где 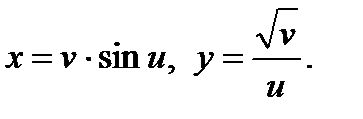
Р е ш е н и е. Находим:
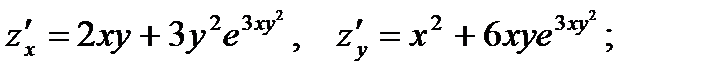
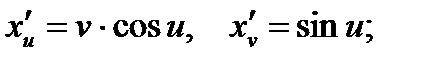
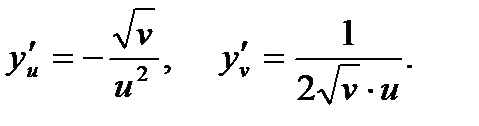
Тогда по формулам вычисления частных производных сложной функции получаем:
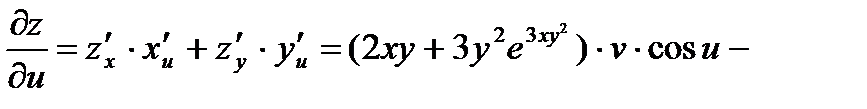
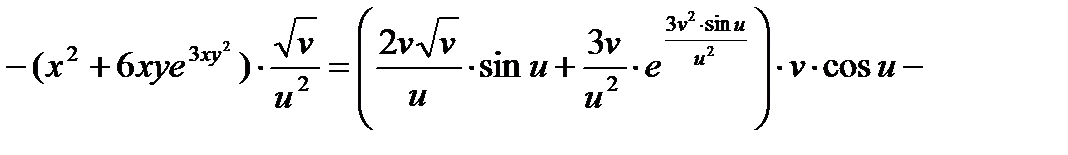
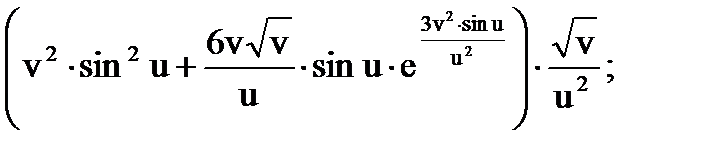
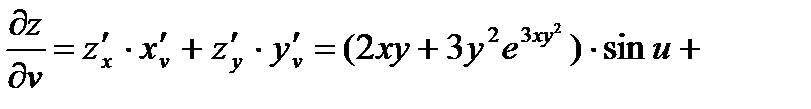
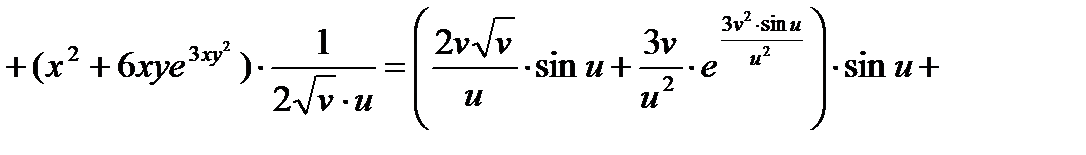
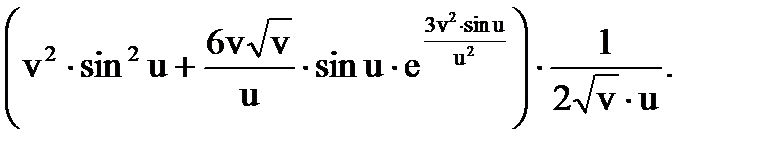
О т в е т: 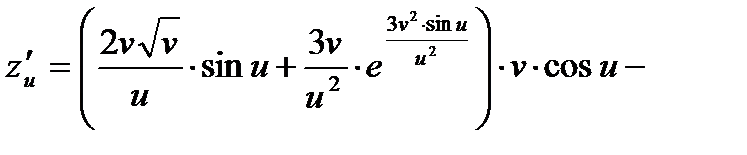
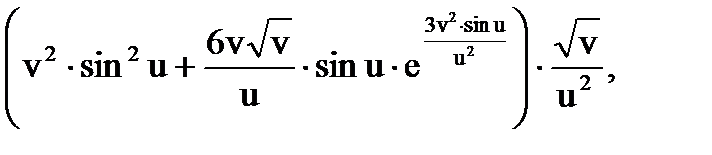
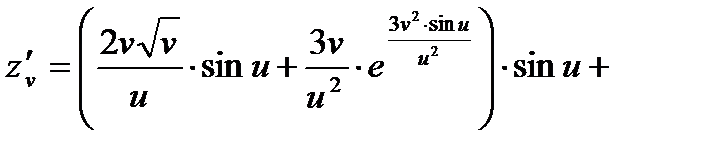
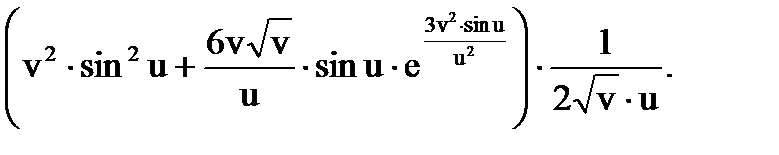
7. ПОЛНАЯ ПРОИЗВОДНАЯ
Т е о р е м а 5. Пусть функции 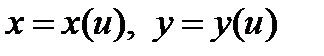 дифференцируемы в некоторой точке
дифференцируемы в некоторой точке 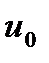 , а функция
, а функция 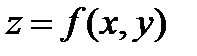 дифференцируема в соответствующей точке
дифференцируема в соответствующей точке 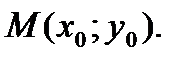 Тогда сложная функция
Тогда сложная функция 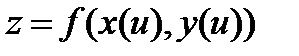 , как функция одной переменной
, как функция одной переменной 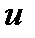 , дифференцируема в точке
, дифференцируема в точке 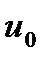 и ее так называемая полная производная в этой точке вычисляется по формуле:
и ее так называемая полная производная в этой точке вычисляется по формуле:
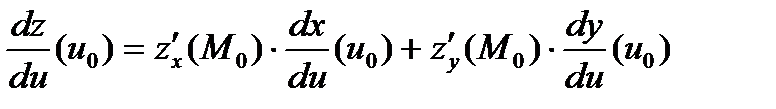 .
.
С л е д с т в и е. Пусть функция 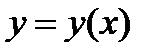 дифференцируема в некоторой точке
дифференцируема в некоторой точке 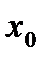 , а функция
, а функция 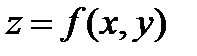 дифференцируема в соответствующей точке
дифференцируема в соответствующей точке 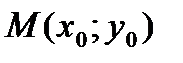 , где
, где 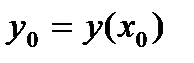 . Тогда сложная функция
. Тогда сложная функция 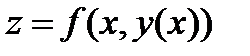 , как функция переменной
, как функция переменной 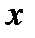 , дифференцируема в точке
, дифференцируема в точке 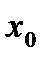 и ее полная производная в этой точке вычисляется по формуле:
и ее полная производная в этой точке вычисляется по формуле:
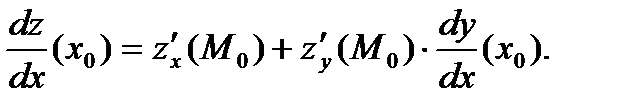
Пример 9. Найти полную производную 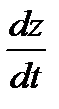 , если
, если 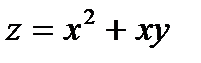 и
и 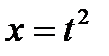 ,
,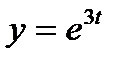 .
.
Решение. В данном случае
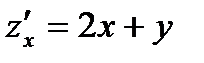 ,
, 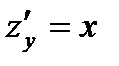 ,
, 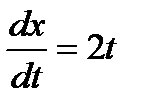 ,
, 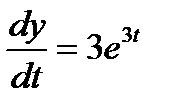 .
.
Поэтому, воспользовавшись формулой вычисления полной производной, находим:
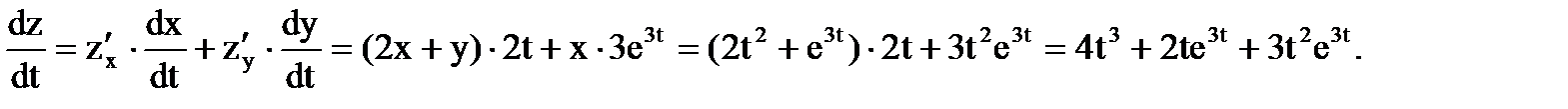
Ответ: 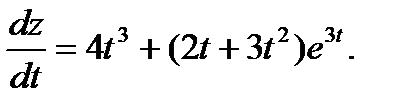
П р и м е р 10. Найти 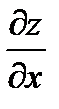 (частную производную) и
(частную производную) и 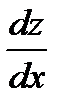 (полную производную), если
(полную производную), если 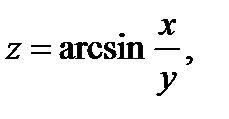 где
где 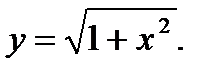
Р е ш е н и е. Вычисляем:
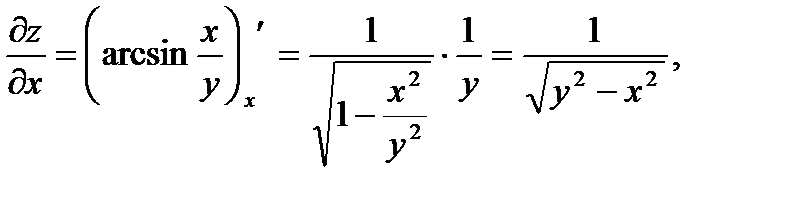
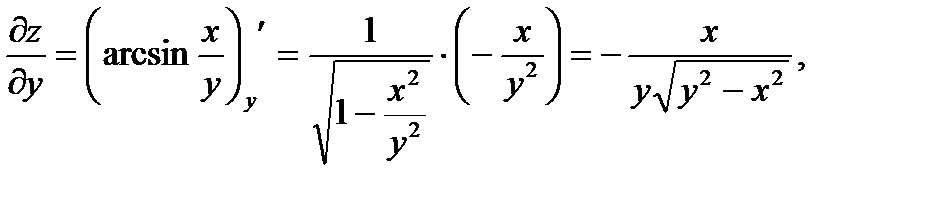
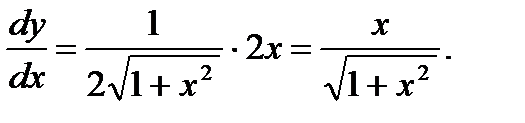
Поэтому находим полную производную:
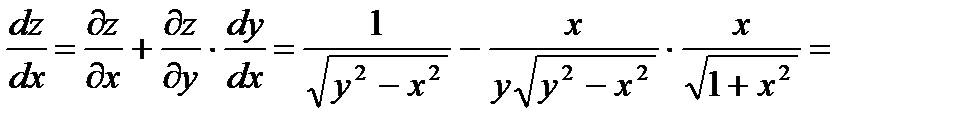
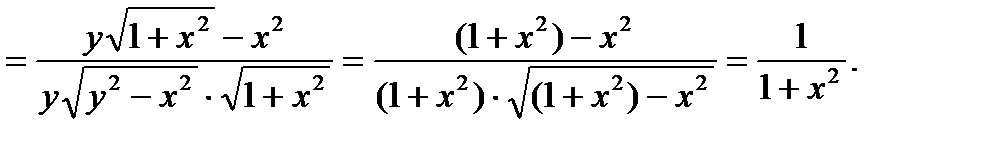
О т в е т: 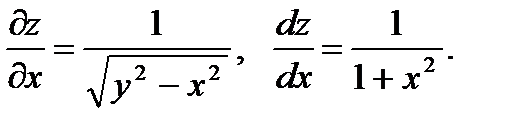
8. ПОЛНЫЙ ДИФФЕРЕНЦИАЛ
О п р е д е л е н и е 15.Полным дифференциалом 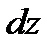 функции
функции 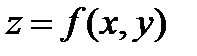 в точке
в точке 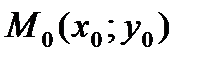 называется выражение вида:
называется выражение вида:
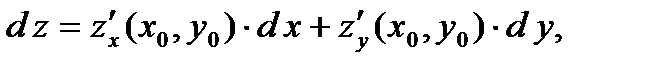 (5)
(5)
где 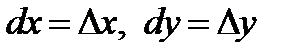 и
и 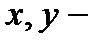 независимые переменные.
независимые переменные.
З а м е ч а н и е 7(свойство инвариантности формы полного дифференциала). Формула (5) справедлива и в случае, когда 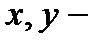 зависимые переменные.
зависимые переменные.
Например, пусть 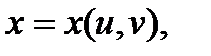
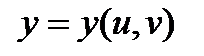 , где
, где 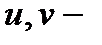 независимые переменные. В этом случае полный дифференциал функции
независимые переменные. В этом случае полный дифференциал функции 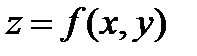 в точке
в точке 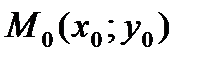 , где
, где 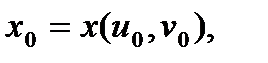
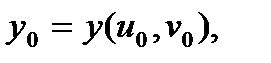 вычисляется по формуле (5) , причем
вычисляется по формуле (5) , причем
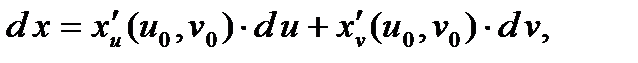
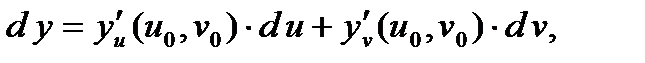 где
где 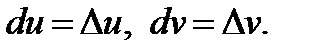
З а м е ч а н и е 8.Правила дифференцирования функции одной переменной сохраняют силу и для функции любого числа переменных. Например, от скольких бы аргументов не зависели функции 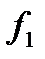 и
и 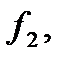 справедливы равенства:
справедливы равенства: 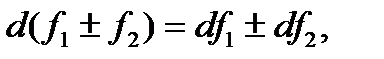
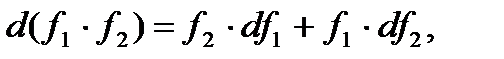
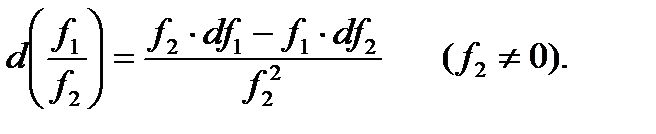
З а м е ч а н и е 9.В точке 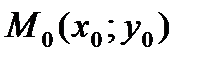 с точностью до бесконечно малых слагаемых высшего порядка относительно
с точностью до бесконечно малых слагаемых высшего порядка относительно 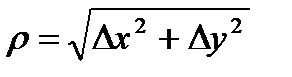 можно приближенно считать:
можно приближенно считать: 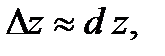 то есть
то есть 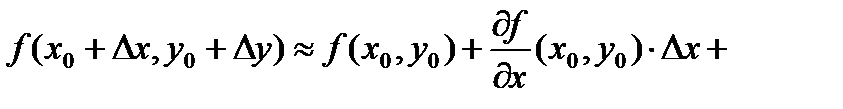
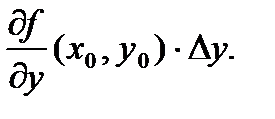
П р и м е р 11. Найти полный дифференциал функции 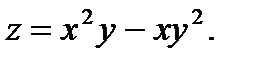
Р е ш е н и е. Предварительно находим: 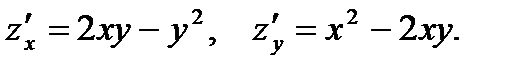 Тогда, воспользовавшись формулой (5), вычисляем
Тогда, воспользовавшись формулой (5), вычисляем
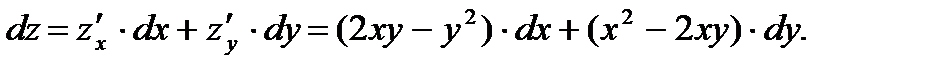
О т в е т: 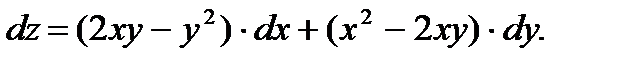
Пример 12. Найти полный дифференциал функции 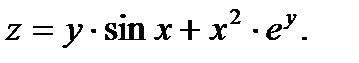
Решение. В данном случае 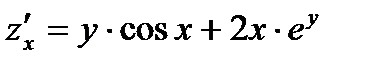 ,
, 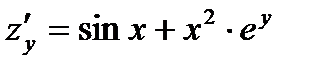 . Поэтому по формуле (5) находим:
. Поэтому по формуле (5) находим: 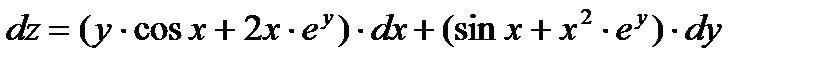 .
.
Ответ: 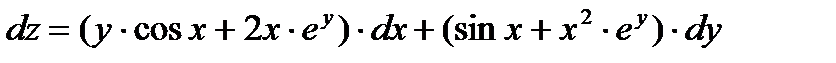 .
.
П р и м е р 13. Вычислить приближенно число 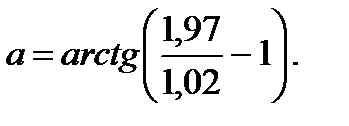
Р е ш е н и е. Рассмотрим функцию 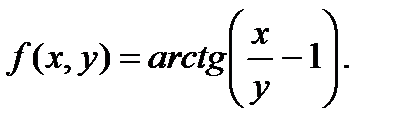 Пусть
Пусть 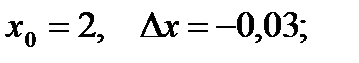
 Тогда
Тогда 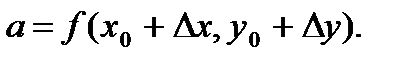 Вычисляем:
Вычисляем:
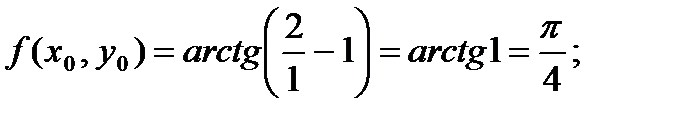
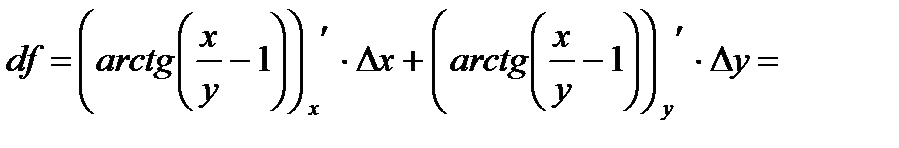
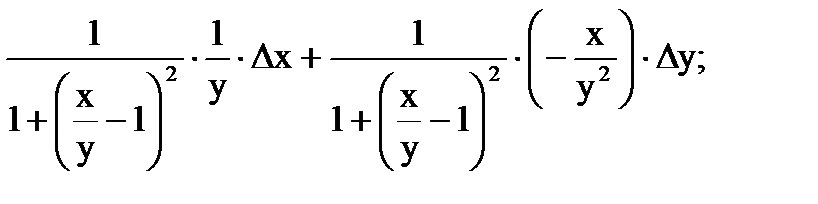
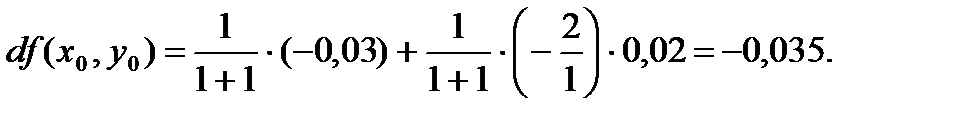
Следовательно, по свойству дифференциала верно приближенное равенство:
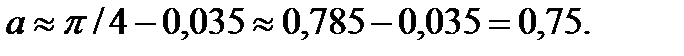
О т в е т: