Коэффициенты взаимосвязи качественных признаков

Для оценки связи качественных признаков необходим коэффициент, к-й имел бы определенный максимум в случае максимальной связи и позволял бы сравнивать между собой разные таблицы по силе связи между признаками. В данном случае нам подходит коэффициент Крамера V.

Базируясь на значении критерия хи-квадрат, коэффициент Крамера позволяет измерять силу связи между двумя категоризованными переменными - измерить ее числом, принимающим значения от 0 до 1, т.е. от полного отсутствия связи до максимальной сильной связи. Коэффициент позволяет сравнить зависимости разных признаков, с тем, чтобы выявить более и менее сильные связи.

Математическое моделирование.

Специфика задач моделирования:

1. история не занимается прогнозированием

2. нет основательных рядов данных, массивов, по которым можно настраивать модель, ограниченность данных

3. комплексная наука (от культуры до экономики).

Причины применения моделей в ист.исследованиях:

1. реконструкция отсутствующих данных по динамике процесса (Пелопонесские войны)

2. оценка роли тех или иных факторов в их действии на результат процесса, проверка предположений

3. теоретический анализ ситуаций.

Модели бывают разных типов (от вербальных до математических). Философские, натурные и др.

Цель моделирования – заменить реальный объект исследования его моделью, а затем исследовать поведение модели, перенося выводы на объект.

Главный вопрос – адекватность модели изучаемому объекту (изоморфность).

Математическая модель – система уравнений, в которой конкретные величины заменяются математически понятными постоянными и переменными величинами, функциями. Для этого применяются дифференциальные, интегральные и алгебраические уравнения.

Система математических соотношений, описывающих изучаемый процесс или явление; в общем смысле такая модель является множеством символических объектов и отношений между ними. (Г.И.Рузавин).

Типы моделей:

(связаны с ситуациями применения моделей)

- имитационные (имитирует характер процесса, допускается много переменных х и уравнений, сложная форма взаимосвязи между ними.

Пример: системы конечно-разностных уравнений)

- статистические (малое число уравнений, большое число переменных, сложные связи между ними, обратные связи трудны для исследования.

Пример: уравнения множественной регрессии, факторный анализ)

- аналитические (математические, одно или несколько уравнений и простая связь между ними.

Пример: дифференциальные уравнения, марковские цепи)

Эти три подхода, вообще говоря, приводят исследователя к построению различных типов теорий. Там, где используется аналитическое моделирование, имеются небольшие возможности для анализа поведения систем с нелинейными или обратными связями. Когда выбрано статистическое моделирование, мы вынуждены оценивать параметры модели из уравнений. Такие модели также имеют ограниченное применение в случае наличия обратных связей. Если используется имитационное моделирование, тогда мы относительно свободны от математических или статистических ограничений. Это может быть чрезвычайно полезно для построения теории: есть возможность учитывать сложные обратные и нелинейные связи. Однако, в этом случае мы ограничены в понимании изучаемой системы пределами экспериментирования с моделью.

Модель Мальтуса – в 18 в. предсказал, что будет перенаселение. Но он не учел, что есть механизмы саморегулирования.

Лотка и Вольтера – модель «хищник-жертва».

Дифференциальные уравнения.

Построение модели, и ее изучение – "прогон" во времени, оценка роли различных факторов, выявление закономерностей – наиболее эффективно осуществляются с помощью формальных методов, например, разностных или дифференциальных уравнений.

Дифференциальное уравнение – связывает между собой независимую переменную х, искомую функцию у и ее производную различных порядков по х. Часто роль независимой переменной играет время t.

Д.У. описывает, в отличие от разностного уравнения, динамику процесса в каждый момент времени.

Общий вид дифференциального уравнения n-го порядка:

F(x, y, y', y'', …, 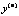) = 0.

Порядок старшей производной определяет порядок уравнения. Например, уравнение y' + y = x имеет порядок 1, уравнение y'' + y'+2y = 0 – порядок 2, уравнение y''' + y'y – x=0 – порядок 3.

Дифференциальное уравнение называется линейным, если неизвестная функция y и ее производные входят в уравнение в первой степени, т.е. с коэффициентами, зависящими только от x, т.е. это уравнение вида:

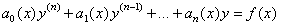
По аналогии с обычным линейным уравнением функции 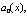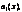…, 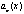называются коэффициентами уравнения, а правая часть, т.е. функция 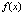– свободным членом. Наиболее простыми из линейных уравнений являются т.н. однородные линейные уравнения, в которых 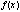=0.

Любая функция 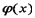, которая, будучи подставлена в дифференциальное уравнение, обращает его в тождество, называется решением этого уравнения. Таким образом, решить дифференциальное уравнение – значит найти все его решения.

Напомним (см. раздел 12.5), что основная задача интегрального исчисления – нахождение функции у, производная которой равна некоторой функции 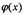. Оказывается, что эта задача сводится как раз к простейшему дифференциальному уравнению вида y' = f(x). Из интегрального исчисления известно, что общим решением этого уравнения является неопределенный интеграл

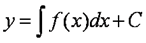где С – произвольная константа. Выбирая различные значения С, можно получить любое частное решение этого уравнения. Чем выше порядок уравнения, тем больше констант входит в его общее решение: в решении уравнения второго порядка – две константы, третьего – три, n-го порядка – n.

Наиболее интересны дифференциальные уравнения, описывающие динамические системы, где в качестве независимой переменной выступает время t. Такие системы используются для описания эволюционных процессов.

Лотка и Вольтерра – модель «хищник-жертва».

КУРС ИНФОРМАТИКА И МАТЕМАТИКА

ЧАСТЬ 2.

МАТЕМАТИКА

Структура курса

• Компьютеризованный статистический анализ

• Моделирование исторических процессов

Система баллов

• Общая сумма – 200 баллов. Из них:

• Информатика – 100 баллов (3 семестр)

• Математика – 100 баллов (4 семестр)

• Баллы по математике:

• Коллоквиум 1 – 25 баллов

• Коллоквиум 2 – 25 баллов

• Экзамен – 50 баллов

• Теория – 25 баллов

• Тестовые задания – 25 баллов

Компьютеризованный статистический анализ

• Дескриптивная статистика - см. ниже;)

• Выборочный метод

• Статистическая проверка гипотез

• Корреляционный анализ

• Регрессионный анализ

• Взаимосвязь качественных признаков

• Многомерный статистический анализ

• Кластерный анализ

• Факторный анализ

• Анализ динамических рядов

Моделирование исторических процессов

• Аналитические модели

• Статистические модели

• Имитационные модели

Статистика

• Статистика – наука, которая изучает массовые общественные явления (прежде всего, социально-экономические), исследование которых связано с количественной характеристикой и выявлением присущих им закономерностей. Предметом статистики являются общие вопросы измерения и анализа массовых количественных отношений и взаимосвязей.

Статистика

• Основной характерной особенностью статистических методов является то, что они не имеют дело с отдельными случаями, объектами, индивидуумами – но всегда с совокупностями, группами, т.е. массовым материалом . Там и тогда, где и когда речь идет о совокупности данных , возможен статистический подсчет и, следовательно, применение статистических методов.

Статистика

• Иногда под статистикой понимают также и статистические данные:

• статистика торговли,

• судебная статистика,

• статистика занятости,

• демографическая статистика (статистика населения),

• медицинская статистика,

• транспортная статистика,

• статистика труда

• и т.д.

Математическая статистика

• Раздел математики, посвященный математическим методам систематизации, обработки и использования статистических данных для научных и практических выводов.

• Математическая статистика тесно связана с теорией вероятностей, изучающей случайные события и случайные процессы.

Теория вероятностей

• Вероятность – числовая характеристика (мера) возможности появления какого-либо определенного события в тех или иных определенных, могущих повторяться неограниченное число раз условиях.

• Вероятность принимает значения в интервале [0; 1] или [0%, 100%].

Теория вероятностей

• Событие, которое наступает в определенных условиях всегда, имеет вероятность 1 или 100%. Оно называется достоверным.

• Событие, которое не наступает в определенных условиях никогда, имеет вероятность 0. Оно называется невозможным.

Теория вероятностей

• На практике представление о вероятности события дает относительная частота (доля) его появления в серии с конечным числом испытаний.

• Чем больше число испытаний, тем ближе значение частоты к вероятности.

Теория вероятностей

• Большую роль в теории вероятностей играет понятие распределения .

• Особую роль играет т.н. нормальное распределение , которое часто реализуется во многих ситуациях, в которых на результат влияет большое количество независимых случайных факторов, среди которых нет сильно выделяющихся.

Теория вероятностей

• Нормальное распределение можно изобразить графически в виде симметричной одновершинной кривой, напоминающей по форме колокол. Высота (ордината) каждой точки этой кривой показывает, как часто встречается соответствующее значение.

МЕТОДЫ МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ

Основные понятия

• Математическая статистика имеет дело с совокупностью объектов , которые обладают некоторым набором признаков (показателей, характеристик). Это т.н. статистическая совокупность.

• Статистическая совокупность может включать все изучаемые объекты (в этом случае она называется генеральной совокупностью ) или только часть объектов (тогда она называется выборкой ).

Основные понятия

• Классическим для математической статистики подходом является представление исходных данных как выборки из реальной или гипотетической генеральной совокупности.

• При этом все результаты анализа интерпретируются как выборочные и ставится задача их оценки в генеральной совокупности.

Основные понятия

• Основные методы математической статистики можно отнести к двум ее разделам:

• теории статистического оценивания параметров и

• теории проверки статистических гипотез.

Типы признаков

• В связи с возможностью измерения все признаки принято делить на две большие группы: количественные и качественные .

• Количественные признаки могут быть измерены для каждого объекта числом

• Качественные признаки не могут быть измерены количественно (выражены числом) для каждого объекта, они указывают (как правило в текстовой форме) категорию, к которой относится тот или иной объект.

Типы признаков

• Наиболее часто в статистике используются количественные признаки (возраст, доход и т.п.)

• С количественными признаками допустимы все арифметические операции, именно для них разработано большинство статистических методов.

Типы признаков

• Однако качественные признаки также допускают измерение: можно подсчитать количество объектов, попадающих в ту или иную категорию данного признака (то есть, подсчитать частоту встречаемости этой категории). Можно также долю этой категории в совокупности, т.е. относительную частоту встречаемости.

Типы признаков

• Таким образом, на уровне совокупности происходит «превращение» качества в количество: для группы людей можно подсчитать число студентов среди них, а это уже количественный показатель, с которым можно выполнять арифметические операции точно так же, например, как со средним возрастом в данной совокупности.

Дескриптивная статистика

• Для более глубокого исследования материала необходимы обобщающие количественные показатели, раскрывающие общие свойства статистической совокупности.

• Дескриптивная или описательная статистика позволяет для каждого показателя заменить всю совокупность его индивидуальных значений некоторыми общими для всех объектов величинами.

Дескриптивная статистика

• Эти обобщенные показатели:

• дают общую картину, показывают тенденцию развития процесса или явления, нивелируя случайные индивидуальные отклонения,

• позволяют сравнивать различные совокупности,

• используются во всех разделах математической статистики при более полном и сложном анализе статистического материала.

Основные статистические характеристики

• Основные статистические характеристики можно разделить на две основные группы :

• меры среднего уровня и

• меры рассеяния (разброса).

Основные статистические характеристики

• Меры среднего уровня дают усредненную характеристику совокупности объектов по определенному признаку (например, средний возраст – характеристика некоторой группы людей).

• Меры рассеяния показывают, насколько хорошо средние значения представляют данную совокупность.

Меры среднего уровня

• К мерам среднего уровня относятся:

• среднее (арифметическое) значение (обозначается Mean или ) ,

• мода (обозначается M o ),

• медиана (обозначается M edian или M е).

Среднее арифметическое значение

• Среднее арифметическое значение – это сумма значений признака у всех объектов совокупности, отнесенная к общему числу объектов, т.е. средним арифметическим значением признака называется величина

где - значение признака у i -го объекта, n – число объектов в совокупности.

Среднее арифметическое значение

• Например, если значения возраста в совокупности (группе) из 5 человек, равны 30, 35, 30, 40 и 30 лет, то для вычисления среднего возраста надо сложить все пять значений и полученную сумму (165) разделить на 5.

• В результате средний возраст получится равным 33.

Мода

• Мода – наиболее часто встречающееся значение признака в данной совокупности объектов.

• Так, в нашем примере значения возраста в совокупности (группе) из 5 человек равны 30, 35, 30, 40 и 30 лет. Таким образом, значение 30 лет встречается 3 раза, 35 лет и 40 лет – по 1 разу. Модой будет то значение, которое встретилось чаще других, т.е. 30 лет.

Медиана

• Медиана – это "серединное" значение признака в том смысле, что у половины объектов значения этого признака меньше медианы, а у другой половины объектов – больше медианы.

• Для того, чтобы найти медиану, необходимо упорядочить все значения признака по возрастанию (или убыванию) и найти то число, которое находится в середине полученного ряда.

Медиана

• В нашем примере упорядоченный по возрастанию (ранжированный) ряд значений выглядит так: 30, 30, 30, 35, 40. Серединой является третье значение (слева и справа от него стоят по два числа).

• Значит, медиана – это 30 лет.

Медиана

• Если в ряду четное число значений, посередине окажутся два числа. Например, в ряду 30, 30, 30, 35, 40, 50 посередине (на третьем и четвертом местах) стоят числа 30 и 35.

• В этом случае в качестве моды можно взять среднее арифметическое из этих чисел, т.е. 32,5 года.

Частотные распределения

• Обычно предполагается, что исходные данные имеют вид таблицы "объекты-признаки", т.е. каждый признак задается для каждого объекта. Однако чем больше объем совокупности, тем чаще повторяются значения признаков у разных объектов.

• Например, в исходных данных много раз встречаются люди одинакового возраста, с одинаковыми профессиями или уровнем образования и т.д.

Частотные распределения

• В этом случае полезно строить распределение признака, которое дает информацию о том, сколько раз встречаются различные значения признака, т.е. каковы их частоты .

• Наиболее адекватное представление о распределении дают упорядоченные значения признака, если речь идет о количественных или ранговых признаках (для номинальных признаков порядок категорий не имеет значения).

Частотные распределения

• Графическое изображение частотного распределения называется гистограммой .

• Гистограмма показывает зависимость частоты встречаемости признака от соответствующего значения или интервала группировки.

• Гистограмма также показывает моду распределения.

Гистограмма

• Для того, чтобы при помощи гистограммы определить моду, надо найти на ней самый высокий столбик. Он соответствует тому значению признака, которое встречается чаще других, т.е. моде.

• В зависимости от характера распределения наибольшую высоту могут иметь несколько столбиков. Так, распределение часто бывает бимодальным . Если мода имеет только одно значение, распределение называется унимодальным .

Гистограмма

• Часто гистограмма используется для сопоставления эмпирического распределения признака с нормальным (для проверки гипотезы о том, что значения данного признака распределены по нормальному закону – очень важному в теории вероятностей типу распределения).

Меры среднего уровня

• Не все меры среднего уровня можно найти для любого признака.

• Если признак номинальный , то для него можно найти только моду (ее значением будет название наиболее часто встречающейся категории номинального признака).

• Если признак ранговый , то кроме моды для него можно найти еще и медиану.

• Однако среднее арифметическое значение можно вычислять только для количественных признаков.

Меры среднего уровня

Количественный признак

Качественный ранговый признак

Качественный номинальный признак

Ср. арифметическое

Медиана

Мода

Медиана

Мода

Меры среднего уровня

• В случае количественных данных все меры среднего уровня измеряются в тех же единицах, что и сам исходный признак.

• Если все значения исходного признака изменятся в несколько раз , то же самое произойдет и со всеми средними величинами для этого признака.

• Если все значения исходного признака изменятся на некоторое число , то же самое произойдет и со всеми средними.

Меры среднего уровня

• Если распределение значений признака близко к нормальному распределению, все три меры среднего уровня (среднее арифметическое, медиана и мода) дают близкие значения.

• Если же имеются значения, сильно отличающиеся от других, то они заметно влияют на среднее арифметическое («притягивают» его к себе), и в таком случае лучше использовать медиану, менее чувствительную к «выпадающим точкам».

Меры среднего уровня

• Например, для значений 30, 30, 30, 35, 40 среднее арифметическое равно 33, а медиана равна 30. Допустим, в результате ошибки последнее число в этом ряду записано неверно: 30, 30, 30, 35, 400. Тогда среднее арифметическое резко увеличится и станет равным 105. Медиана же не изменится (не изменится и мода).

• Следовательно, при наличии «выпадающих точек» медиана предпочтительнее.

Меры рассеяния

• Все меры рассеяния показывают, насколько сильно варьируют значения признака (а точнее – их отклонения от среднего) в данной совокупности.

• Чем меньше значение меры разброса, тем ближе значения признака у всех объектов к своему среднему значению, а значит, и друг к другу.

• Если величина меры разброса равна нулю, значения признака у всех объектов одинаковы.

Меры рассеяния

• К мерам рассеяния относятся:

• среднее квадратическое или стандартное отклонение – мера разброса значений признака около среднего арифметического значения (принятые обозначения: Std.Dev. - standard deviation или s ).

• дисперсия признака ( s 2 )

• коэффициент вариации – отношение стандартного отклонения к среднему арифметическому, выраженное в процентах (обозначается в статистике буквой V ).

Среднее квадратическое отклонение

• Наиболее часто используется среднее квадратическое (или стандартное) отклонение s .

• Величина этого отклонения вычисляется по формуле:

• где - значение признака у i -го объекта, - среднее арифметическое значение, n – число объектов в совокупности.

Среднее квадратическое отклонение

• Среднее квадратическое отклонение измеряется, как и среднее арифметическое, в тех же единицах, что и сам исходный признак.

• Если все значения признака изменить в несколько раз , точно так же изменится и стандартное отклонение, однако если все значения признака увеличить (уменьшить) на некоторую величину , его стандартное отклонение не изменится .

Дисперсия

• Наряду со стандартным отклонением часто пользуются дисперсией , равной его квадрату, однако на практике она является менее удобной мерой, поскольку единицы измерения дисперсии не соответствуют единицам измерения признака (попробуйте представить рубли или тонны в квадрате!).

Коэффициент вариации

• Коэффициент вариации вычисляется по формуле:

• Смысл его состоит в том, что он, в отличие от среднего квадратического отклонения, измеряет не абсолютную, а относительную меру разброса значений признака в статистической совокупности.

Коэффициент вариации

• Сравнение распределений признаков на основании таких характеристик, как среднее арифметическое значение и стандартное отклонение, затруднительно во многих случаях, например, когда эти признаки измеряются в разных единицах.

• Но даже если признаки и имеют одинаковый смысл, прямое сравнение возможно лишь для средних арифметических значений, но не для стандартных отклонений.

Коэффициент вариации

• Например, в одной группе среднее квадратическое отклонение по доходу равно 400 руб., а во второй – 2000 руб., то есть в 5 раз больше, чем в первой.

• Можно ли сделать вывод, что первая группа гораздо более однородна по величине дохода, чем вторая, – или следует обратить внимание на то, что и средние значения показателей неодинаковы?

Коэффициент вариации

• Если учесть, что средний доход в первой группе – 800 руб., а во второй – 8000 руб., то получим, что в первой группе V = 50%, а во второй V = 25%, т.е. в относительном измерении как раз вторая группа значительно более однородна.

Коэффициент вариации

• Если в некоторой совокупности коэффициент вариации не превышает 30%, эта совокупность является однородной по данному признаку.

• Если коэффициент вариации превышает 50%, совокупность является неоднородной . Такую совокупность разбивают на более однородные части.

• Если коэффициент вариации находится в диапазоне 30-50%, то решение об однородности принимает исследователь.

Меры рассеяния

• Все меры рассеяния (среднее квадратическое отклонение, дисперсию и коэффициент вариации) можно вычислять только для количественных признаков.

• При этом величина среднего квадратического отклонения и дисперсии меняются при изменении единиц измерения признака, а величина коэффициента вариации – не изменяется.

• Коэффициент вариации может превышать 100%.

Меры рассеяния

• Если величина меры разброса равна нулю, значения признака у всех объектов одинаковы.

Нормальное распределение

• Наиболее адекватное представление о распределении дают упорядоченные значения признака.

Нормальное распределение

• Графическое изображение частотного распределения называется гистограммой .

Нормальное распределение

• Часто гистограмма используется для сопоставления эмпирического распределения признака с нормальным распределением (для проверки гипотезы о том, что значения данного признака распределены по нормальному закону – очень важному в теории вероятностей типу распределения).

Нормальное распределение

• Понятие нормального распределения играет в статистике важную роль, поскольку для корректного использования многих статистических методов необходимо, чтобы признаки подчинялись нормальному закону.

• Если взглянуть на гистограмму распределения признака в программе S tatistica , можно увидеть на ее фоне плавную симметричную колоколообразную кривую. Это и есть теоретическая кривая нормального распределения.

Гистограмма и кривая нормального распределения

Нормальное распределение

• Нормальное распределение можно изобразить графически в виде симметричной одновершинной кривой, напоминающей по форме колокол.

• Высота (ордината) каждой точки этой кривой показывает, как часто встречается соответствующее значение. Эти ординаты обобщают введенное ранее понятие частоты отдельных значений признака или интервалов значений.

Нормальное распределение

• Если эмпирическое распределение признака по своему характеру близко к нормальному, то форма гистограммы напоминает (конечно, в огрубленном виде) форму нормальной кривой и "стремится" к этой нормальной кривой, если увеличивать число интервалов, одновременно уменьшая их величину.

Нормальное распределение

• Многие эмпирические распределения реальных величин действительно близки к нормальным. Считается, что величина распределяется нормально, если на характер распределения влияет много факторов, причем ни один из этих фактором не является определяющим.

Нормальное распределение

• Например, такие признаки, как возраст или рост людей в достаточно больших совокупностях распределены нормально, а зарплата или доход демонстрируют сильно "скошенное" влево распределение (т.е. пик такого распределения находится не посередине, а смещен в сторону меньших значений признака).

Нормальное распределение

• Форма и положение нормальной кривой полностью определяются двумя параметрами: средним арифметическим значением и средним квадратическим отклонением.

• Вершина кривой соответствует среднему арифметическому значению, т.е. наиболее часто встречаются значения, близкие к среднему, а по мере удаления от него частота падает (редко встречаются значения, сильно отклоняющиеся от среднего).

Нормальное распределение

• Геометрически вероятность значений, меньших данного, изображается площадью под кривой распределения слева от этого значения. Площадь под всей кривой равна 1, что соответствует полной достоверности, т.е. вероятности того, что признак вообще принимает какое-то (любое) значение.

Нормальное распределение

• Ввиду своей важности для практических приложений функция нормального распределения табулирована , т.е. в соответствующих таблицах многочисленных учебников каждому значению признака ставится в соответствие определенная вероятность.

Нормальное распределение

• Разные признаки несравнимы между собой, так как измеряются в разных единицах и соответственно имеют разный масштаб и диапазон значений.

• Но если вместо исходных значений признаков использовать их отклонения от среднего, деленные на стандартное отклонение, все признаки, распределенные по нормальному закону, приводятся к стандартному виду (с нулевым средним и стандартным отклонением, которое равно 1).

Нормальное распределение

• Пример. Какова вероятность того, что отклонение значения нормально распределенного признака от своего среднего арифметического более чем в три раза превысит s - стандартное отклонение этого признака?

• Оказывается, вероятность того, что значение признака отклонится от среднего в любую сторону на столь значительную величину, очень мала и составляет менее 0,3%.

Нормальное распределение

• Значит, подавляющее большинство (99,7%) значений признака попадет в диапазон от –3 s до +3 s .

• Следовательно, в интервале [–3 s , +3 s ] находятся практически все значения признака (в статистике это называется правилом "трех сигм" ).

Нормальное распределение

• В статистике можно не только вычислять вероятность стандартизованных отклонений признака, но и наоборот – по определенной вероятности вычислять эти отклонения.

• Например, можно определить величину стандартизованного отклонения, вероятность превзойти которую (по абсолютной величине) равна всего 5%.

Нормальное распределение

• Оказывается, при нормальном распределении с вероятностью 95% значение x отличается от своего среднего не больше чем на 1,96 ? или примерно на 2 ? .

• Значит, в интервал

попадет 95% всех значений признака.

Выборочный метод

Основные понятия

• Множество всех единиц статистической совокупности носит название генеральной совокупности . Многие задачи статистического анализа связаны с описанием больших совокупностей объектов.

• Зачастую на практике по тем или иным причинам невозможно рассмотреть все элементы таких совокупностей. В этом случае ограничиваются изучением лишь некоторой части генеральной совокупности. Эта часть называется выборочной совокупностью или выборкой .

• Полученные при изучении выборки результаты стремятся распространить на всю генеральную совокупность.

• Для этого выборка должна быть не любой произвольной частью генеральной совокупности, а такой ее частью, которая достаточно правильно отражает основные параметры этой совокупности.

• Таким образом, выборка должна быть репрезентативной (представи - тельной).

• Каким образом можно добиться репрезентативности выборки, т.е. того, чтобы она правильно отражала основные свойства, присущие генеральной совокупности?

• Ответ кажется, на первый взгляд, довольно парадоксальным: выборка должна быть случайной . Что это значит?

• Случайность никоим образом не отождествляется со стихийностью или произвольностью отбора – напротив, случайность означает то, что все объекты генеральной совокупности должны иметь равные шансы попасть в выборку .

• Наиболее простым является случайный отбор, например, при помощи обычной жеребьевки .

• Для случайного отбора часто используются т.н. таблицы случайных чисел.

• Для более обширных, но достаточно однородных совокупностей используется механический отбор (применявшийся еще в земской статистике).

• Для неоднородных совокупностей с определенной структурой чаще применяется типический отбор .

• Существуют и другие методы, в том числе – комбинации разных способов отбора на нескольких этапах построения выборочной совокупности.

* * *

• Однако никакая, даже самым тщательным образом сформированная выборка, не может дать точного знания о генеральной совокупности.

• Таким образом, в выборочных результатах всегда присутствуют ошибки . Эти ошибки можно разделить на два класса:

• случайные,

• систематические.

• К случайным ошибкам относятся отклонения выборочных характеристик от генеральных (например, отклонения среднего значения признака в выборке от среднего значения этого признака в генеральной совокупности.

• Случайные ошибки обусловлены самой природой выборочного метода, и поэтому они неизбежны .

• Однако величина случайной ошибки поддается вычислению (оценке).

• Систематические ошибки, наоборот, не носят случайного характера; они связаны с откло