Предмет математической статистики, её основные разделы. Понятие о статистическом распределении. Нормальное распределение. В каких условиях случайная величина распределена нормально?

Статистика – наука, узучающая совокупн. масс. явл-я с целью выявления закономерн. и изуч-я их с помощью обобщенных показателей. Все методы математической статистики можно отнести к двум основным ее разделам: теории статистического оценивания параметров и теории проверки статистических гипотез.

Разделы:

1. дескриптивная статистика

2. выборочный метод, доверительные интервалы

3. корреляционный анализ

4. регрессионный анализ

5. анализ качественных признаков

6. многомерный статистический анализ:

а) кластерный

б) факторный

7. анализ временных рядов

8. дифференциальные уравнения

9. математическое моделирование исторических процессов

Распределение:

- теоретическое (бесконечно много объектов и они ведут себя идеально)

- эмпирическое (реальные данные, которые можно выстроить в гистограмму)

Нормальное распределение – когда характер распределения влияют много факторов, и ни один из них не является определяющим. Особенно часто используется на практике.

Нормальное распределение можно изобразить графически в виде симметричной одновершинной кривой, напоминающей по форме колокол. Высота (ордината) каждой точки этой кривой показывает, как часто встречается соответствующее значение.

Понятие о выборочном методе. Репрезентативная выборка, методы её формированияю Два вида ошибок выборки. Доверительная вероятность.

Выборка - Это множество объектов из генеральной совокупности (всего множества объектов, св-ва которых нужно изучить), свойства которых мы измеряем и обрабатываем для того, чтобы иметь представление о свойствах генеральной совокупности.

Выборка:

- репрезентативная

- случайная

Механическая выборка – сходна со случайной выборкой (кажд. 10й, 20й и т.п.).

+ естественная(то, что осталось от ГС с течением времени) выборки.

Репрезентативная выборка – точно отражает свойства генеральной совокупности.

Чтобы выборка правильно отражала основные свойства, присущие генеральной совокупности, она должна быть случайной, т.е. все объекты генеральной совокупности должны иметь равные шансы попасть в выборку

Выборки формируются с помощью спец. методик. Наиболее простым является случайный отбор, например, при помощи обычной жеребьевки (для небольших совокупностей) или с использованием таблиц случайных чисел. Для более обширных, но достаточно однородных совокупностей используется механический отбор (применявшийся еще в земской статистике). Для неоднородных совокупностей с определенной структурой чаще применяется типический отбор. Существуют и другие методы, в том числе - комбинации разных способов отбора на нескольких этапах построения выборочной совокупности.

В выборочных результатах всегда присутствуют ошибки. Эти ошибки можно разделить на два класса: случайные и систематические. К первым относятся случайные отклонения выборочных характеристик от генеральных, обусловленные самой природой выборочного метода. Величина случайной ошибки поддается вычислению (оценке). Систематические ошибки, наоборот, не носят случайного характера; они связаны с отклонением структуры выборки от реальной структуры генеральной совокупности. Систематические ошибки появляются тогда, когда нарушается основное правило случайного отбора - обеспечение для всех объектов равных шансов поапсть в выборку. Ошибки этого рода статистика не умеет оценивать.

Основными источниками систематических ошибок являются: а) неадекватность сформированной выборки задачам исследования; б) незнание характера распределения в генеральной совокупности и, как следствие, нарушение в выборке структуры генеральной совокупности; в) сознательный отбор наиболее удобных и выигрышных элементов генеральной совокупности.

Доверительная вероятность – вероятность того, что значение рассчитываемого коэф-та для ген. Совокупности попадет в доверительный интервал. Чеи больше ДВ, тем больше ДИ.

Доверительная вероятность. Средняя (стандартная) и предельная ошибки выборки. Доверительный интервал для оценки среднего значения в генеральной совокупности. Проверка гипотезы о статистической значимости различия двух выборочных средних.

Доверительный интервал - тот значений рассчитываемого коэф-та, в к-й, мы считаем,должно попасть это значение для ген. Совокуп-ти.

Неизбежный разброс выборочных средних вокруг генеральной средней (т.е. стандартное отклонение выборочных средних) называется стандартной ошибкой выборки m, которая выражается формулой 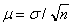(s - среднее квадратическое отклонение, n - объем выборки). стандартная ошибка выборки тем меньше, чем меньше величина s(которая характеризует разброс значений признака) и чем больше объем выборки n.

Если выборочный метод используется для работы с неколичественными данными, то роль среднего арифметического значения в совокупности играет доля или частота qпризнака. Доля вычисляется как отношение числа объектов, обладающих данным признаком (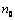), к числу объектов во всей совокупности: 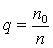. Роль меры разброса играет величина .

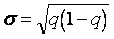В этом случае стандарная ошибка выборки m вычисляется по формуле:

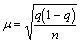Точность и надежность оценки параметров генеральной совокупности по выборке находятся в обратной зависимости: чем больше точность (т.е. чем меньше предельная ошибка и чем уже доверительный интервал), тем меньше надежность такой оценки (степень уверенности). И наоборот - чем ниже точность оценки, тем выше ее надежность. Часто доверительный интервал строят для надежности 95%, соответственно предельная ошибка выборки обычно равна удвоенной средней ошибке m..

Доверительный интервал для оценки среднего значения в генеральной совокупности:

X(г.с.) = x(выб.) +-Δ = x(выб.) +- tμ = X(выб.) +- σ(г.с.)/√n

Критерий для разности средних значений

Часто возникает задача сравнения двух выборочных средних с целью проверки гипотезы о том, что эти выборки получены из одной и той же генеральной совокупности, а реальные расхождения в значениях выборочных средних объясняются случайностями выборок.

Испытуемую гипотезу можно сформулировать следующим образом: различие между выборочными средними случайно, т.е. генеральные средние в обоих случаях равны. В качестве статистической характеристики снова используется величина t, предсталяющая собой разность выборочных средних, деленную на усредненную стандартную ошибку среднего по обеим выборкам.

Фактическое значение статистической характеристики сравнивается с критическим значением, соответсвующим выбранному уровню значимости. Если фактическое значение больше, чем критическое, испытуемая гипотеза отклоняется, т.е. различие между средними считается значимым (существенным).

Корреляционная связь. Линейный коэффициент корреляции, его формула, пределы его значений. Коэффициент детерминации, его содержательный смысл. Понятие о статистической значимости коеффициента корреляции.

Коэффициент корреляции показывает, насколько тесно две переменных связаны между собой.

Коэффициент корреляции r принимает значения в диапазоне от -1 до +1. Если r = 1, то между двумя переменными существует функциональная положительная линейная связь, т.е. на диаграмме рассеяния соответствующие точки лежат на одной прямой с положительным наклоном. Если r = -1,то между двумя переменными существует функциональная отрицательная зависимость. Если r = 0,то рассматриваемые переменные линейно независимы, т.е. на диаграмме рассеяния облако точек "вытянуто по горизонтали".

Уравнение регрессии и коэффициент корреляции целесообразно вычислять лишь в том случае, когда зависимость между переменными может хотя бы приближенно считаться линейной. В противном случае результаты могут быть совершенно неверными, в частности коэффициент корреляции может оказаться близким к нулю при наличии сильной взаимосвязи. В особенности это характерно для случаев, когда зависимость имеет явно нелинейный характер (например, зависимость между переменными приблизительно описывается синусоидой или параболой). Во многих случаях эту проблему можно обойти, преобразовав исходные переменные. Однако, чтобы догадаться о необходимости подобного преобразования, т.е. для того чтобы узнать, что данные могут содержать сложные формы зависимости, их желательно “увидеть”. Именно поэтому исследование взаимосвязей между количественными переменными обычно должно включать просмотр диаграмм рассеяния.

Коэффициенты корреляции можно вычислять и без предварительного построения линии регрессии. В этом случае вопрос о интерпретации признаков как результативных и факторных, т.е. зависимых и независимых, не ставится, а корреляции понимается как согласованность или синхронность одновременного изменения значений признаков при переходе от объекта к объекту.

Если объекты характеризуются целым набором количественных признаков, можно сразу построить т.н. матрицу корреляции, т.е. квадратную таблицу, число строк и столбцов которой равно числу признаков, а на пересечении каждых строки и столбца стоит коэффициент корреляции соответствующей пары признаков.

Коэффициент корреляции не имеет содержательной интерпретации. Однако его квадрат, называемый коэффициентом детерминации (R²), имеет.

Коэффициентом детерминации (R²) – это показатель того, насколько изменения зависимого признака объясняются изменениями независимого. Более точно, это доля дисперсии независимого признака, объясняемая влиянием зависимого.

Если две переменные функционально линейно зависимы (точки на диаграмме рассеяния лежат на одной прямой), то можно сказать, что изменение переменной y полностью объясняется изменением переменной x, а это как раз тот случай, когда коэффициент детерминации равен единице (при этом коэффициент корреляции может быть равен как 1, так и -1). Если две переменные линейно независимы (метод наименьших квадратов дает горизонтальную прямую), то переменная y своими вариациями никоим образом "не обязана" переменной x – в этом случае коэффициент детерминации равен нулю. В промежуточных случаях коэффициент детерминации указывает, какая часть изменений переменной y объясняется изменением переменной x (иногда удобно представлять эту величину в процентах).

Парная и множественная линейная регрессия. Коэффициент множественной корреляции. Содержательный смысл коэффициента регрессии, его значимость, понятие о t-статистике. Содержательный смысл коэффициента детерминации R2.

Регрессионный анализ - Статистический метод, позволяющий строить объясняющие модели на основе взаимодействия признаков.

Самым простым случаем взаимосвязи является парная взаимосвязь, т.е. связь между двумя признаками. При этом предполагается, что взаимосвязь двух переменных носит, как правило, причинный характер т.е. одна из них зависит от другой. Первая (зависимая) называется в регрессионном анализе результирующей, вторая (независимая) -факторной. Следует заметить, что не всегда можно однозначно определить, какая из двух переменных является независимой, а какая - зависимой. Часто связь может рассматриваться как двунаправленная.

Уравнение парной регрессии: y = kx + b.

Чаще всего на зависимую переменную действуют сразу несколько факторов, среди которых трудно выделить единственный или главный Так, к примеру, доход предприятия зависит одновременно от двух факторов производства - числа рабочих и энерговооруженности. Причем оба этих фактора сами не являются независимыми друг от друга.

Уравнение множественной регрессии: y = k₁·x₁ + k₂·x₂ + … + b,

где x₁, x₂, . . . – независимые переменные, от которых в той или иной степени зависит исследуемая (результирующая) переменная y;

k₁, k₂ . . . – коэффициенты при соответствующих переменных (коэффициенты регрессии), показывающие, насколько изменится значение результирующей переменной при изменении отдельной независимой переменной на единицу.

Уравнение множественной регрессии задает регрессионную модель, объясняющую поведение зависимой переменной. Никакая регрессионная модель не в состоянии указать, какая переменная является зависимой (следствием), а какие – независимыми (причинами).

R – множественный коэф. корреляции, измеряет совокупность воздействия независимых признаков, тесноту связи результирующего признака со всей совокупностью независимых признаков, выраженных в %.

Показывает какова доля учтенных признаков в отделении результата, т.е. на сколько % вариация признака у объясняется вариациями учтенных признаков Х1, Х2, Х3.

Содержательный смысл коэффициента регрессии – коэф.регрессии b показывает, на сколько в среднем изменится результирующий признак у при увеличении независимого признака х на ед-цу измерения. Не может быть = 0.

T-статистика показывает уровень стат. значимости кажд. ккоэф-та регресии, т.е. его устойчивость по отношению к выборке.

T = b/ΔbСтатистически значимыми явл-ся t>2. Чем больше коэф-т, тем лучше.

через R² мы делаем заключение о том, на сколько % учтенные признаки объясняют результат.

Методы многомерного статистического анализа. Факторный анализ, цели его использования. Понятие о факторных нагрузках и факторных весах, пределы их значений; доля суммарной дисперсии, объясняемой факторами.

Многомерный статистический анализ.Его цель: построение упрощенного укрупненного ряда объектов.

МСА:

- кластерный анализ

- факторный анализ

- многомерное шкалирование

В основе факторного анализа лежит идея о том, что за сложными взаимосвязями явно заданных признаков стоит относительно более простая структура, отражающая наиболее существенные черты изучаемого явления, а "внешние" признаки являются функциями скрытых общих факторов, определяющих эту структуру.

Цель: переход от большего числа признаков к небольшому числу факторов.

в факторном анализе все величины, входящие в факторную модель, стандартизированы, т.е. являются безразмерными величинами со средним арифметическим значением 0 и средним квадратическим отклонением 1.

Коэффициент взаимосвязи между некоторым признаком и общим фактором, выражающий меру влияния фактора на признак, называется факторной нагрузкойданного признака по данному общему фактору. Это число в интервале от -1 до 1. Чем дальше от 0, тем более сильная связь. Значение факторной нагрузки по некоторому фактору, близкое к нулю, говорит о том, что этот фактор практически на данный признак не влияет.

Значение (мера проявления) фактора у отдельного объекта называется факторным весом объекта по данному фактору. Факторные веса позволяют ранжировать, упорядочить объекты по каждому фактору. Чем больше факторный вес некоторого объекта, тем больше в нем проявляется та сторона явления или та закономерность, которая отражается данным фактором. Факторы являются стандартизованными величинами, не могут быть = нулю. Факторные веса, близкие к нулю, говорят о средней степени проявления фактора, положительные – о том, что эта степень выше средней, отрицательные – о том. что она ниже средней.

Таблица факторных весов имеет n строк по числу объектов и k столбцов по числу общих факторов. Положение объектов на оси каждого фактора показывает, с одной стороны, тот порядок, в котором они ранжированы по этому фактору, а с другой стороны, равномерность или же неравномерность в их расположении, наличие скоплений точек, изображающих объекты, что дает возможность визуально выделять более или менее однородные группы.

11. Виды качественных признаков. Номинальные признаки, примеры из исторических источников. Таблица сопряженности. Коэффициент связи номинальных признаков, пределы его значений.

Качественные (или категориальные) данные делятся на два типа: ранговые и номинальные.

Номинальные данные представлены категориями, для которых порядок абсолютно не важен. Для них не определен никакой другой способ сравнения, кроме как на буквальное совпадение/несовпадение.

Примеры номинальных переменных:

· Национальность: англичанин, белорус, немец, русский, японец и пр.

· Род занятий: служащий, врач, военный, учитель и т.д.

· Профиль образования: гуманитарное, техническое, медицинское, юридическое и т.д.

Если в случае с уровнем образования мы еще могли сравнивать людей в терминах "лучше-хуже" или "выше-ниже", то теперь мы лишены даже этой возможности; единственный корректный способ сравнения ‑ это говорить, что данные персоналии "все являются историками", или "все не являются юристами".

Своеобразие качественных данных не означает, что их нельзя анализировать с помощью математических и статистических методов.

Таблицы сопряженности

Таблицей сопряженности называется прямоугольная таблица, по строкам которой указываются категории одного признака (например, разные социальные группы), а по столбцам - категории другого (например, партийная принадлежность). Каждый объект совокупности попадает в какую-либо из клеток этой таблицы в соответствии с тем, в какую категорию он попадает по каждому из двух признаков. Таким образом, в клетках таблицы стоят числа, представляющие собой частоты совместной встречаемости категорий двух признаков (число людей, принадлежащих конкретной социальной группе и входящих в определенную партию). В зависимости от характера распределения этих частот внутри таблицы можно судить о том, существует ли связь между признаками. Что означает связь между социальным статусом и партийной принадлежностью? В данном случае о наличии связи свидетельствовало бы наличии определенных политических пристрастий у членов разных социальных групп. Формально говоря, эта связь понимается как более частая (или наоборот, редкая) совместная встречаемость отдельных комбинаций категорий по сравнению с ожидаемой встречаемостью - ситуацией чисто случайного попадания объектов туда (например, более высокая доля крестьян в партии трудовиков, а дворян - в партии кадетов, чем доли этих социальных групп во всей совокупности депутатов Думы).

12. Виды качественных признаков. Ранговые признаки, примеры из исторических источников. В каких пределах находятся значения коэффициента ранговой корреляции? Какие коэффициенты следует использовать для оценки связи рангового и номинального признаков?

Качественные (или категориальные) данные делятся на два типа: ранговые и номинальные.

Ранговые данные представлены категориями, для которых можно указать порядок, т.е. категории сравнимы по принципу "больше-меньше" или "лучше-хуже".

Примеры ранговых переменных:

· Оценки на экзаменах имеют явно выраженную ранговую природу и выражаются категориями типа: "отлично", "хорошо", "удовлетворительно" и т.д.

· Уровень образования может быть представлен как набор категорий: "высшее", "среднее" и т.п.

Несомненно, мы можем ввести ранговую шкалу и с ее помощью упорядочить всех людей, для которых мы знаем их уровень образования или балл на экзамене. Однако, верно ли, что оценка "хорошо" на столько же хуже, чем "отлично", насколько оценка "удовлетворительно" хуже, чем "хорошо"? Несмотря на то, что формально, в случае с оценками, можно получить разницу в баллах, вряд ли корректно измерять расстояние от "отличника" до "хорошиста" пользуясь теми же правилами, что для расстояния от Москвы до Петербурга. В случае с уровнем образования особенно отчетливо видно, что простые вычисления невозможны, поскольку не существует единого правила вычитания "среднего" уровня образования из "высшего", даже, если мы присвоим высшему образованию код "3", а среднему – код "2".

Своеобразие качественных данных не означает, что их нельзя анализировать с помощью математических и статистических методов.Ряд объектов, упорядоченных в соответствии со степенью проявления некоторого свойства, называют ранжированным, каждому числу такого ряда присваивается ранг.

Меры взаимосвязи между парой признаков, каждый из которых ранжирует изучаемую совокупность объектов, называются в статистике коэффициентами ранговой корреляции.

Эти коэффициенты строятся на основе следующих трех свойств:

· если ранжированные ряды по обоим признакам полностью совпадают (т.е. каждый объект занимает одно и то же место в обоих рядах), то коэффициент ранговой корреляции должен быть равен +1, что означает полную положительную корреляцию:

· если объекты в одном ряду расположены в обратном порядке по сравнению со вторым, коэффициент равен -1, что означает полную отрицательную корреляцию;

· в остальных ситуациях значения коэффициента заключены в интервале [-1, +1]; возрастание модуля коэффициента от 0 до 1 характеризует увеличение соответствия между двумя ранжированными рядами.

Указанными свойствами обладают коэффициенты ранговой корреляции Спирменаr и Кедаллаt.

Коэффициент Кедалла дает более осторожную оценку корреляции, чем коэффициент Спирмена (числовое значение t всегда меньше, чем r).

Дифференциальные уравнения.

Построение модели, и ее изучение – "прогон" во времени, оценка роли различных факторов, выявление закономерностей – наиболее эффективно осуществляются с помощью формальных методов, например, разностных или дифференциальных уравнений.

Дифференциальное уравнение – связывает между собой независимую переменную х, искомую функцию у и ее производную различных порядков по х. Часто роль независимой переменной играет время t.

Д.У. описывает, в отличие от разностного уравнения, динамику процесса в каждый момент времени.

Общий вид дифференциального уравнения n-го порядка:

F(x, y, y', y'', …, 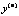) = 0.

Порядок старшей производной определяет порядок уравнения. Например, уравнение y' + y = x имеет порядок 1, уравнение y'' + y'+2y = 0 – порядок 2, уравнение y''' + y'y – x=0 – порядок 3.

Дифференциальное уравнение называется линейным, если неизвестная функция y и ее производные входят в уравнение в первой степени, т.е. с коэффициентами, зависящими только от x, т.е. это уравнение вида:

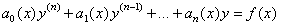
По аналогии с обычным линейным уравнением функции 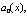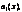…, 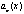называются коэффициентами уравнения, а правая часть, т.е. функция 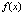– свободным членом. Наиболее простыми из линейных уравнений являются т.н. однородные линейные уравнения, в которых 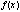=0.

Любая функция 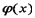, которая, будучи подставлена в дифференциальное уравнение, обращает его в тождество, называется решением этого уравнения. Таким образом, решить дифференциальное уравнение – значит найти все его решения.

Напомним (см. раздел 12.5), что основная задача интегрального исчисления – нахождение функции у, производная которой равна некоторой функции 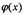. Оказывается, что эта задача сводится как раз к простейшему дифференциальному уравнению вида y' = f(x). Из интегрального исчисления известно, что общим решением этого уравнения является неопределенный интеграл

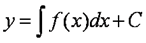где С – произвольная константа. Выбирая различные значения С, можно получить любое частное решение этого уравнения. Чем выше порядок уравнения, тем больше констант входит в его общее решение: в решении уравнения второго порядка – две константы, третьего – три, n-го порядка – n.

Наиболее интересны дифференциальные уравнения, описывающие динамические системы, где в качестве независимой переменной выступает время t. Такие системы используются для описания эволюционных процессов.

Модель Мальтуса – в 18 в. предсказал, что будет перенаселение. Но он не учел, что есть механизмы саморегулирования.

Лотка и Вольтерра – модель «хищник-жертва».

КУРС ИНФОРМАТИКА И МАТЕМАТИКА

ЧАСТЬ 2.

МАТЕМАТИКА

Структура курса

• Компьютеризованный статистический анализ

• Моделирование исторических процессов

Система баллов

• Общая сумма – 200 баллов. Из них:

• Информатика – 100 баллов (3 семестр)

• Математика – 100 баллов (4 семестр)

• Баллы по математике:

• Коллоквиум 1 – 25 баллов

• Коллоквиум 2 – 25 баллов

• Экзамен – 50 баллов

• Теория – 25 баллов

• Тестовые задания – 25 баллов

Компьютеризованный статистический анализ

• Дескриптивная статистика - см. ниже;)

• Выборочный метод

• Статистическая проверка гипотез

• Корреляционный анализ

• Регрессионный анализ

• Взаимосвязь качественных признаков

• Многомерный статистический анализ

• Кластерный анализ

• Факторный анализ

• Анализ динамических рядов

Моделирование исторических процессов

• Аналитические модели

• Статистические модели

• Имитационные модели

Статистика

• Статистика – наука, которая изучает массовые общественные явления (прежде всего, социально-экономические), исследование которых связано с количественной характеристикой и выявлением присущих им закономерностей. Предметом статистики являются общие вопросы измерения и анализа массовых количественных отношений и взаимосвязей.

Статистика

• Основной характерной особенностью статистических методов является то, что они не имеют дело с отдельными случаями, объектами, индивидуумами – но всегда с совокупностями, группами, т.е. массовым материалом . Там и тогда, где и когда речь идет о совокупности данных , возможен статистический подсчет и, следовательно, применение статистических методов.

Статистика

• Иногда под статистикой понимают также и статистические данные:

• статистика торговли,

• судебная статистика,

• статистика занятости,

• демографическая статистика (статистика населения),

• медицинская статистика,

• транспортная статистика,

• статистика труда

• и т.д.

Математическая статистика

• Раздел математики, посвященный математическим методам систематизации, обработки и использования статистических данных для научных и практических выводов.

• Математическая статистика тесно связана с теорией вероятностей, изучающей случайные события и случайные процессы.

Теория вероятностей

• Вероятность – числовая характеристика (мера) возможности появления какого-либо определенного события в тех или иных определенных, могущих повторяться неограниченное число раз условиях.

• Вероятность принимает значения в интервале [0; 1] или [0%, 100%].

Теория вероятностей

• Событие, которое наступает в определенных условиях всегда, имеет вероятность 1 или 100%. Оно называется достоверным.

• Событие, которое не наступает в определенных условиях никогда, имеет вероятность 0. Оно называется невозможным.

Теория вероятностей

• На практике представление о вероятности события дает относительная частота (доля) его появления в серии с конечным числом испытаний.

• Чем больше число испытаний, тем ближе значение частоты к вероятности.

Теория вероятностей

• Большую роль в теории вероятностей играет понятие распределения .

• Особую роль играет т.н. нормальное распределение , которое часто реализуется во многих ситуациях, в которых на результат влияет большое количество независимых случайных факторов, среди которых нет сильно выделяющихся.

Теория вероятностей

• Нормальное распределение можно изобразить графически в виде симметричной одновершинной кривой, напоминающей по форме колокол. Высота (ордината) каждой точки этой кривой показывает, как часто встречается соответствующее значение.

МЕТОДЫ МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ

Основные понятия

• Математическая статистика имеет дело с совокупностью объектов , которые обладают некоторым набором признаков (показателей, характеристик). Это т.н. статистическая совокупность.

• Статистическая совокупность может включать все изучаемые объекты (в этом случае она называется генеральной совокупностью ) или только часть объектов (тогда она называется выборкой ).

Основные понятия

• Классическим для математической статистики подходом является представление исходных данных как выборки из реальной или гипотетической генеральной совокупности.

• При этом все результаты анализа интерпретируются как выборочные и ставится задача их оценки в генеральной совокупности.

Основные понятия

• Основные методы математической статистики можно отнести к двум ее разделам:

• теории статистического оценивания параметров и

• теории проверки статистических гипотез.

Типы признаков

• В связи с возможностью измерения все признаки принято делить на две большие группы: количественные и качественные .

• Количественные признаки могут быть измерены для каждого объекта числом

• Качественные признаки не могут быть измерены количественно (выражены числом) для каждого объекта, они указывают (как правило в текстовой форме) категорию, к которой относится тот или иной объект.

Типы признаков

• Наиболее часто в статистике используются количественные признаки (возраст, доход и т.п.)

• С количественными признаками допустимы все арифметические операции, именно для них разработано большинство статистических методов.

Типы признаков

• Однако качественные признаки также допускают измерение: можно подсчитать количество объектов, попадающих в ту или иную категорию данного признака (то есть, подсчитать частоту встречаемости этой категории). Можно также долю этой категории в совокупности, т.е. относительную частоту встречаемости.

Типы признаков

• Таким образом, на уровне совокупности происходит «превращение» качества в количество: для группы людей можно подсчитать число студентов среди них, а это уже количественный показатель, с которым можно выполнять арифметические операции точно так же, например, как со средним возрастом в данной совокупности.

Дескриптивная статистика

• Для более глубокого исследования материала необходимы обобщающие количественные показатели, раскрывающие общие свойства статистической совокупности.

• Дескриптивная или описательная статистика позволяет для каждого показателя заменить всю совокупность его индивидуальных значений некоторыми общими для всех объектов величинами.

Дескриптивная статистика

• Эти обобщенные показатели:

• дают общую картину, показывают тенденцию развития процесса или явления, нивелируя случайные индивидуальные отклонения,

• позволяют сравнивать различные совокупности,

• используются во всех разделах математической статистики при более полном и сложном анализе статистического материала.

Основные статистические характеристики

• Основные статистические характеристики можно разделить на две основные группы :

• меры среднего уровня и

• меры рассеяния (разброса).

Основные статистические характеристики

• Меры среднего уровня дают усредненную характеристику совокупности объектов по определенному признаку (например, средний возраст – характеристика некоторой группы людей).

• Меры рассеяния показывают, насколько хорошо средние значения представляют данную совокупность.

Меры среднего уровня

• К мерам среднего уровня относятся:

• среднее (арифметическое) значение (обозначается Mean или ) ,

• мода (обозначается M o ),

• медиана (обозначается M edian или M е).

Среднее арифметическое значение

• Среднее арифметическое значение – это сумма значений признака у всех объектов совокупности, отнесенная к общему числу объектов, т.е. средним арифметическим значением признака называется величина

где - значение признака у i -го объекта, n – число объектов в совокупности.

Среднее арифметическое значение

• Например, если значения возраста в совокупности (группе) из 5 человек, равны 30, 35, 30, 40 и 30 лет, то для вычисления среднего возраста надо сложить все пять значений и полученную сумму (165) разделить на 5.

• В результате средний возраст получится равным 33.

Мода

• Мода – наиболее часто встречающееся значение признака в данной совокупности объектов.

• Так, в нашем примере значения возраста в совокупности (группе) из 5 человек равны 30, 35, 30, 40 и 30 лет. Таким образом, значение 30 лет встречается 3 раза, 35 лет и 40 лет – по 1 разу. Модой будет то значение, которое встретилось чаще других, т.е. 30 лет.

Медиана

• Медиана – это "серединное" значение признака в том смысле, что у половины объектов значения этого признака меньше медианы, а у другой половины объектов – больше медианы.

• Для того, чтобы найти медиану, необходимо упорядочить все значения признака по возрастанию (или убыванию) и найти то число, которое находится в середине полученного ряда.

Медиана

• В нашем примере упорядоченный по возрастанию (ранжированный) ряд значений выглядит так: 30, 30, 30, 35, 40. Серединой является третье значение (слева и справа от него стоят по два числа).

• Значит, медиана – это 30 лет.

Медиана

• Если в ряду четное число значений, посередине окажутся два числа. Например, в ряду 30, 30, 30, 35, 40, 50 посередине (на третьем и четвертом мест