Внешняя характеристика выпрямителя
Заменив в (3.16) выражение 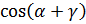 выражением из (3.9), получим уравнение внешней характеристики для режима нагрузок, при которых
выражением из (3.9), получим уравнение внешней характеристики для режима нагрузок, при которых 

где  ,
,  – действующее или эффективное значение фазной ЭДС вторичной обмотки трансформатора. Как видно из (3.17), для каждого значения угла управления
– действующее или эффективное значение фазной ЭДС вторичной обмотки трансформатора. Как видно из (3.17), для каждого значения угла управления 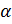 выпрямитель имеет свою внешнюю характеристику.
выпрямитель имеет свою внешнюю характеристику.
Семейство внешних характеристик для различных значений 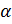 представляет собой семейство параллельных прямых, проведенных под некоторым углом наклона к оси абсцисс, рис.3.8.
представляет собой семейство параллельных прямых, проведенных под некоторым углом наклона к оси абсцисс, рис.3.8.
Рис.3.8 Семейство внешних характеристик выпрямителя
Однако, характеристика выпрямителя описывается полученным уравнением (3.17) не при всех режимах, а только в области нормальных нагрузок. С увеличением тока, как следует из соотношения (3.9), увеличивается угол коммутации 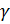 . Когда угол
. Когда угол 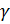 достигает величины π/3, закономерность работы выпрямителя меняется. В области нормальных нагрузок
достигает величины π/3, закономерность работы выпрямителя меняется. В области нормальных нагрузок  в периоде выпрямленного напряжения можно различить два интервала: внекоммутационный и коммутациой. Внекоммутационный интервал, когда два вентиля проводят ток, имеет длительность
в периоде выпрямленного напряжения можно различить два интервала: внекоммутационный и коммутациой. Внекоммутационный интервал, когда два вентиля проводят ток, имеет длительность  ; второй интервал, во время которого происходит коммутация, имеет длительность
; второй интервал, во время которого происходит коммутация, имеет длительность 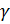 . Когда угол
. Когда угол 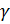 достигает значения
достигает значения  , длительность первого интервала становится равной нулю. Как только закрывается вентиль одной фазы, в этот же момент отпирается очередной вентиль в другой группе. Таким образом, у выпрямителя непрерывно чередуются интервалы одновременной работы трех вентилей.
, длительность первого интервала становится равной нулю. Как только закрывается вентиль одной фазы, в этот же момент отпирается очередной вентиль в другой группе. Таким образом, у выпрямителя непрерывно чередуются интервалы одновременной работы трех вентилей.
При дальнейшем увеличении тока нагрузки угол коммутации продолжает оставаться неизменным и равным  , однако, начинает меняться угол регулирования. Это объясняется тем, что к моменту отпирания очередного вентиля потенциал его анода оказывается отрицательным и вентиль не может открыться до тех пор, пока не закроется предыдущий вентиль и потенциал анода очередного вентиля не станет положительным. Так, угол регулирования делается как бы больше того, который задан системой управления, и с увеличением нагрузки продолжает возрастать.
, однако, начинает меняться угол регулирования. Это объясняется тем, что к моменту отпирания очередного вентиля потенциал его анода оказывается отрицательным и вентиль не может открыться до тех пор, пока не закроется предыдущий вентиль и потенциал анода очередного вентиля не станет положительным. Так, угол регулирования делается как бы больше того, который задан системой управления, и с увеличением нагрузки продолжает возрастать.
В результате, при дальнейшем увеличении тока нагрузки, среднее значение выпрямленного напряжения начинает быстро уменьшаться.
Закономерность изменения внешней характеристики для режимов предельных токов определяется из уравнений (3.9) и (3.14):

Преобразовав разность и сумму косинусов углов в правой части и положив
 , получим:
, получим:


Далее учтем, что  Тогда вместо (3.18) можем записать:
Тогда вместо (3.18) можем записать:


Возводя в квадрат каждое из этих равенства и складывая почленно левые и правые части, получим

Последнее выражение представляет уравнение эллипса, оси которого совпадают с осями координат 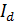 и
и 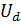 , оно выражает зависимость
, оно выражает зависимость  , в параметрической форме, для предельной кривой, ограничивающей линейные участки характеристик
, в параметрической форме, для предельной кривой, ограничивающей линейные участки характеристик  в виде зависимостей (3.17).
в виде зависимостей (3.17).
Следует заметить, что предельные значения тока 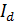 , лежащие на эллиптической кривой, часто значительно превышают нормальные нагрузки для выпрямителя.
, лежащие на эллиптической кривой, часто значительно превышают нормальные нагрузки для выпрямителя.
