Столбчатые и круговые диаграммы

Методический комментарий

Продолжается формирование умения работать с диаграммами. С этой целью рассматриваются более сложные по конструкции столбчатые диаграммы. Кроме того, учащиеся знакомятся с новым видом диаграмм — круговыми. Они получают представление о том, что на круговых диаграммах удобно изображать информацию, характеризующую соотношение между частями целого, которая обычно выражена в процентах.

В данном пункте рассматриваются столбчатые диаграммы нового вида, которые позволяют наглядно представить развитие некоторого явления или процесса. Затем на основе рассмотрения типичной для нашей жизни ситуации вводятся круговые диаграммы. Учащиеся получают некоторое представление о приёме построения круговых диаграмм с помощью распределения площади круга на сектора, площади которых отвечают величинам данных, выраженных в процентах. Однако главным остаётся развитие умения читать готовые диаграммы.

При объяснении материала и выполнении упражнений особое внимание обращается на формирование умения делать выводы и принимать решения. Развитию данного умения способствует проведение несложных социологических исследований, тематика которых доступна учащимся этого возраста. С приёмами их проведения учащиеся знакомились в 5 классе. В рабочей тетради даётся тема такого исследования и приводится таблица для записи получаемой информации. При желании можно выбрать любую другую тему, отвечающую интересам класса. В малоинициативном классе такие исследования можно провести на уроке под руководством учителя. В более активном классе лучше всего сбор и представление данных поручить самим учащимся, сформировав для этого рабочие группы.

Комментарий к упражнениям

127.55% больше половины, поэтому подходящую диаграмму выбираем из диаграмм 1 и 3. Подходит диаграмма 1, так как на ней есть сектор, примерно составляющий треть круга, что соответствует 30%, приходящимся на остальные деревья.

Глава 2. Прямые на плоскости и в пространстве (7 уроков)

Примерное поурочное планирование учебного материала

Пункт учебника	Число уроков	Рабочая тетрадь	Характеристика основных видов деятельности учащихся
2.1. Пересекающиеся прямые		1—6 (с. 56—58)	Распознаватьслучаи взаимного расположения двух прямых, а также вертикальные углы. Определять углы, образованные двумя пересекающимися прямыми. Изображатьдве пересекающиеся прямые, строитьпрямую, перпендикулярную данной
2.2. Параллельные прямые		7—15 (с. 59—61)	Распознаватьслучаи взаимного расположения двух прямых на плоскости и в пространстве, а также параллельные стороны в многоугольниках. Изображатьдве параллельные прямые, строить прямую, параллельную данной с помощью чертёжных инструментов. Анализировать способ построения параллельных прямых, пошагово заданный рисунками, выполнять построения; осуществлятьсамоконтроль, проверяя соответствие полученного изображения заданному. Формулироватьутверждения о взаимном расположении двух прямых, свойствах параллельных прямых
2.3. Расстояние		16—25 (с. 62—65)	Измерять расстояние между двумя точками, от точки до прямой, между двумя параллельными прямыми, от точки до плоскости. Строитьпараллельные прямые с заданным расстоянием между ними, а также геометрическое место точек, обладающее определённым свойством
Обзор и контроль

Основные цели: создать у учащихся зрительные образы основных конфигураций, связанных с взаимным расположением прямых; научить строить параллельные и перпендикулярные прямые; научить находить расстояния от точки до прямой и между двумя параллельными прямыми; научить находить углы, образованные двумя пересекающимися прямыми.

Обзор главы. Основные рассматриваемые в главе конфигурации, связанные с прямыми, изображены на рисунке 2.

Учащиеся учатся распознавать и воспроизводить эти конфигурации и решать несложные задачи, связанные с ними.

В 5 классе учащиеся научились строить и измерять углы, устанавливать их равенство. Теперь они должны научиться видеть пары равных углов, образующихся при пересечении двух прямых, а также пары углов, дополняющих друг друга до развёрнутого угла. Целесообразно, чтобы эти факты были установлены учащимися опытным путём. Для этого надо взять лист бумаги, провести на нём две пересекающиеся прямые, обозначить получившиеся углы цифрами 1, 2, 3, 4 и разрезать лист по этим прямым. Теперь с этими углами надо организовать практическую работу: убедиться наложением в равенстве углов, составить различные развёрнутые углы. После этого надо обратиться к чертежу и поработать с ним: закрасить одним и тем же цветом равные углы или отметить их одинаковыми дугами и т. д.

При выполнении упражнений, связанных с углами, образованными пересекающимися прямыми, учащимся необходимо восстановить навыки работы с транспортиром и угольником, вспомнить о свойствах клетчатой бумаги, полезно также попрактиковаться в определении и изображении углов на глаз, без использования чертёжных инструментов.

Наиболее сложной из указанных конфигураций является третья. Она выступает в качестве основы для рассмотрения способа построения параллельных прямых. При желании учитель может ввести оборот речи «две параллельные и секущая», однако называть специальными терминами образовавшиеся углы не следует. Умение указывать равные углы в данной конфигурации является скорее желаемым результатом, чем обязательным.

Кроме того, в данном разделе расширяется понятие «расстояние» за счёт введения понятия «расстояние от точки до фигуры» и его частного случая — расстояния от точки до прямой, расстояния между параллельными прямыми, а также расстояния от точки до плоскости. Учащиеся учатся строить точки на заданном расстоянии от прямой, проводить параллельные прямые с заданным расстоянием между ними и т. д. Следует обратить внимание на то, что задачи, связанные с расстоянием между двумя точками, будут рассмат­риваться и в дальнейшем в различных конфигурациях. Это будут не просто две произвольные «одинокие» точки плоскости, а центры окружностей, две ближайшие или наиболее удалённые точки окружностей, середины отрезков; множество точек, удалённых от заданной на расстояние, определяемое равенством или неравенством; точка, равноудалённая от двух других точек, и т. д.

Принципиально важный случай, требующий особого внимания, — это расстояние от точки до прямой. Рассмотрение его необходимо организовать в виде практической работы. Понятно, что ближайшей к точке А точкой прямой будет та, которой «достигнет» одна из окружностей с центром в точке А (рис. 3), как круги на воде от брошенного камня. (Ведь все точки окружности одинаково удалены от центра, точки внутри круга расположены ближе к центру, а точки вне круга — дальше от центра.) Учащиеся сами с помощью угольника должны убедиться, что прямая, проходящая через центр окружности и найденную ближайшую точку на этой прямой, ей перпендикулярна. Отсюда ясно, что расстояние от точки до прямой измеряется по перпендикуляру. Этот вывод надо запомнить и пользоваться им в дальнейшем.

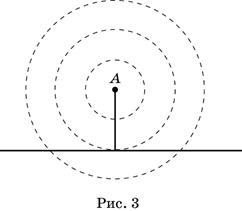
В описанном фрагменте учащиеся, по сути дела, встретились с понятием «касательная к окружности». В явном виде это понятие вводится в п. 5.1 «Окружность и прямая».

Развитие пространственных представлений в процессе изучения материала этой главы происходит при работе с моделью куба, в ходе которой используются изученные в теме понятия (поиск параллельных, пересекающихся, скрещивающихся рёбер куба; сопоставление длины диагонали грани и её стороны и т. д.).

Материалы для контроля.

Пособие «Контрольные работы». Проверочные работы:

1. Пересекающиеся прямые. 2. Параллельные прямые. 3. Расстояние.

Пересекающиеся прямые

Комментарий к упражнениям

143. При пересечении двух прямых образуются четыре угла, сумма которых равна 180° + 180° = 360°. Значит, четвёртый угол равен
360° – 254° = 106°.

146. Задача приводит к следующей гипотезе: угол между биссектрисами данных углов равен 90°.

Очень хорошо, если учащиеся придут к такой гипотезе; доказательство в общем виде не предполагается. Однако если учитель сочтёт возможным рассмотреть обоснование в общем случае, то это можно сделать так: предложить учащимся закрасить угол АОС, например, красным цветом, а угол СОВ — синим. Тогда два красных и два синих угла составляют развёрнутый угол, а искомый угол NOM — его половину, так как составлен из половины красного угла и половины синего.

Параллельные прямые

Комментарий к упражнениям

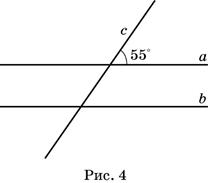
157. Целесообразно начать с аналогичного задания из рабочей тетради, при выполнении которого учащиеся смогут подписывать величины углов непосредственно на рисунке (рис. 4). Эта и другие подобные задачи должны всегда начинаться с анализа данной конфигурации — две параллельные прямые пересечены третьей. Прямая с пересекает прямую а под углом, равным 55°. Значит, и прямую b она пересекает под таким же углом. (Учащиеся показывают соответствующий угол на чертеже и подписывают его величину.) Теперь мы можем обратиться к другой знакомой конфигурации — две пересекающиеся прямые.

161. 1) Начать рассуждение надо с того, что среди трёх прямых могут быть параллельные прямые. Если все три прямые параллельны друг другу, то число точек пересечения равно нулю. Если среди них есть одна пара параллельных прямых, то третья прямая пересечёт каждую из них, и число точек пересечения будет равно двум. Теперь рассмотрим три прямые, среди которых нет параллельных. Если две прямые пересекаются, то третья прямая, пересекающая первые две, может проходить или не проходить через их точку пересечения. В первом случае имеем одну точку пересечения, во втором — три.

2) Надо проанализировать все случаи пересечения трёх прямых и увидеть, что наибольшее число точек пересечения получается тогда, когда никакие две прямые не параллельны друг другу и не проходят через уже имеющуюся точку пересечения. Следовательно, чтобы получить максимально возможное число точек пересечения четырёх прямых, нужно начертить три прямые, пересекающиеся в трёх точках, и провести четвёртую прямую, пересекающую каждую из первых трёх. Понятно, что к трём точкам пересечения, уже имеющимся, добавятся ещё три (по числу прямых). Итого
6 точек.

Расстояние

Комментарий к упражнениям

177. Идея задачи (и ряда задач, ей аналогичных) заключается в том, что если от каждой части целого взять половину, то вместе они составят половину от целого. В данном случае расстояние между серединами отрезков АС и СВ составляет половину длины отрезка АВ, так как равно длине оставшейся его части. Чтобы сделать идею решения более наглядной, можно обвести отрезок АС,например, красным карандашом, а СВ — синим. Легко видеть, что отрезок между серединами отрезков и остальная часть отрезка АВ состоят из половины красного и половины синего отрезков, а следовательно, их длины равны и составляют половину длины отрезка АВ.

Глава 3. Десятичные дроби (9 уроков)

Примерное поурочное планирование учебного материала

Пункт учебника	Число уроков	Рабочая тетрадь	Дидактические материалы	Характеристика основных видов деятельности учащихся
3.1. Десятичная запись дробей		23—37 (с. 11—15)	О-11, О-12, П-9	Записыватьичитать десятичные дроби. Представлять десятичную дробь в виде суммы разрядных слагаемых. Моделировать десятичные дроби рисунками. Переходить от десятичных дробей к соответствующим обыкновенным со знаменателями 10, 100, 1000 и т. д. и наоборот. Изображатьдесятичные дроби точками на координатной прямой
3.2. Десятичные дроби и метрическая система мер		—	О-14	Использовать десятичные дроби для перехода от одних единиц измерения к другим, объяснять значения десятичных приставок, используемых для образования названий единиц в метрической системе мер
3.3. Перевод обыкновенной дроби в десятичную		—	О-13	Формулироватьпризнак обратимости обыкновенной дроби в десятичную, применять его для распознавания дробей, для которых возможна (или невозможна) десятичная запись. Представлять обыкновенные дроби в виде десятичных. Приводить примеры эквивалентных представлений дробных чисел
3.4. Сравнение десятичных дробей		38—44 (с. 16—18)	О-15, «Проверь себя», П-19	Распознавать равные десятичные дроби. Объяснять на примерах приём сравнения десятичных дробей. Сравниватьиупорядочиватьдесятичные дроби. Сравнивать обыкновенную и десятичную дроби, выбирая подходящую форму записи данных чисел. Выявлятьзакономерность в построении последовательности десятичных дробей. Решатьзадачи-исследования, основанные на понимании поразрядного принципа десятичной записи дробных чисел
Обзор и контроль

Основные цели: сформировать понятие десятичной дроби; выработать навыки чтения, записи и сравнения десятичных дробей, обращения обыкновенной дроби в десятичную.

Обзор главы. Данная глава является вводной в крупную тему курса «Десятичные дроби». В ней излагаются основные теоретические сведения. При изучении этой главы формируются основополагающие базовые умения. Учащиеся знакомятся с десятичными дробями как со специальным способом записи обыкновенных дробей со знаменателем вида 10ⁿ, распространяющим на дробные числа идею десятичной нумерации. Они узнают о существовании разрядов, в которых указываются доли единицы, и приобретают первичные навыки работы с новыми символами: учатся понимать и читать соответствующие записи; записывать дроби, знаменателями которых являются степени числа 10, в виде десятичных дробей; изображать десятичные дроби точками на координатной прямой; сравнивать их. Важным с точки зрения развития практических умений является обучение использованию десятичных дробей для выражения одних единиц измерения через другие, кратные им единицы.

Характерной особенностью этой главы (как, впрочем, и следующей) является изложение материала с постоянной опорой на знание учащихся об обыкновенных дробях. Акцентируется внимание на том, что десятичные дроби — это специальный способ записи обыкновенных дробей определённого вида, следовательно, в силе остаются все известные факты об обыкновенных дробях, но знакомые алгоритмы (например, алгоритм сравнения дробей) видоизменяются и упрощаются. Важным в идейном отношении является рассмотрение критерия обратимости обыкновенной дроби в десятичную. Заметим, что вопрос о связи обыкновенных и десятичных дробей будет ещё раз рассмотрен в курсе алгебры 9 класса в теме «Действительные числа».

Материалы для контроля.

Пособие «Контрольные работы». Зачёт 2. Десятичные дроби.

Пособие «Тематические тесты». Тест 4. Десятичные дроби.

Десятичная запись дробей

Методический комментарий

Прочное усвоение материала этого пункта — необходимая предпосылка для успешного формирования практических навыков работы с десятичными дробями. Если, например, ученик ошибается при записи под диктовку таких дробей, как 0,07; 30,105, то понятно, что у него будут постоянные затруднения в ходе изучения всей темы.

Материал пункта содержит несколько смысловых фрагментов. Сначала учащиеся знакомятся с идеей десятичной записи дробных чисел и узнают названия новых разрядов. Завершается первый фрагмент разъяснением правила чтения десятичных дробей. Обращаем внимание учителя на группу вопросов, относящихся к этому фрагменту. Такого рода вопросы (и особенно такие, как первый) следует предлагать учащимся в качестве устных заданий на протяжении нескольких уроков. Это поможет ученикам в осознании структуры десятичной записи дробного числа, в запоминании названий её разрядов.

В следующем фрагменте рассматриваются приёмы перехода от десятичной дроби к соответствующей обыкновенной и записи обыкновенной дроби со знаменателем 10, 100, 1000 и т. д. в виде десятичной. Эти приёмы разъясняются на примерах. Безошибочному выполнению перехода от одной формы записи к другой поможет правило, которое учащиеся безусловно должны запомнить и привыкнуть постоянно использовать для самоконтроля: в десятичной дроби после запятой столько же цифр, сколько нулей в знаменателе соответствующей ей обыкновенной дроби. (Заметим, что навыки использования специальных приёмов самоконтроля при изучении курса математики способствуют и формированию соответствующего общеинтеллектуального качества личности, заключающегося в умении осуществлять анализ собственных действий, самопроверку и самоконтроль в процессе выполнения разнообразной деятельности.) Для выработки навыков перехода от десятичной дроби к обыкновенной и наоборот можно использовать серии упражнений из рабочей тетради (23, 24, 27, 28) и дидактических материалов (2—6).

В последнем фрагменте рассматривается вопрос об изображении десятичных дробей точками на координатной прямой. Этот материал содержательно нацелен не столько на выработку навыка, сколько на более глубокое осознание и понимание поразрядного состава десятичной дроби. Заметим также, что умение ориентироваться на координатной прямой будет полезно при формировании навыков сравнения и упорядочивания дробей.

Разнообразить и дополнить упражнения учебника помогут задания из рабочей тетради (30—37) и дидактических материалов (О-12).

Комментарий к упражнениям

182—184. Назначение этих упражнений — формирование навыка чтения десятичных дробей и запоминание названий разрядов в десятичной записи.

186. в) Сначала нужно выделить целую часть числа, а затем уже представить его в виде десятичной дроби. Например: 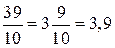. В дальнейшем при выполнении заданий подобного рода ученики смогут пользоваться свёрнутым алгоритмом: при делении на 10 отделять запятой справа одну цифру, при делении на 100 — две цифры и т. д.

190. Есть разные способы выполнения этого задания. Можно сначала выполнить сложение, записав сумму в виде обыкновенной дроби, а потом перейти к десятичной записи. Например, в случае «в» будем иметь:

.

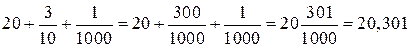В то же время ответ можно получить сразу, если увидеть, что в каждом случае мы, по существу, имеем представление некоторой десятичной дроби в виде суммы разрядных слагаемых. Так, запись 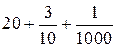означает, что целая часть соответствующей десятичной дроби равна 20, что в разряде десятых у неё 3 единицы, разряд сотых отсутствует (т. е. в нём должна стоять цифра 0), в разряде тысячных одна единица. Из этого рассуждения ясно, что .

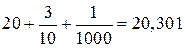191, 193. По существу, учащиеся должны выполнять на содержательном уровне действия с десятичными дробями.

194. Из условия следует, что десятичная дробь может быть записана какими-либо двумя из трёх указанных цифр или всеми тремя цифрами. Если использовать только две цифры, то получим следующие шесть десятичных дробей:

1,2; 1,3; 2,1; 2,3; 3,1; 3,2.

Чтобы не ошибиться при записи десятичных дробей, содержащих все три цифры, удобно рассуждать так. Сделаем «заготовку», записав все возможные трёхзначные натуральные числа, которые могут быть составлены их этих трёх цифр. Всего таких чисел шесть:

123, 132, 213, 231, 312, 321.

Теперь надо в каждое число «поставить» запятую. Это можно сделать двумя способами. Запятая может отделять слева или одну цифру, или две. Поэтому каждое число «раздваивается». Получаем ещё 12 десятичных дробей:

1,23; 12,3; 1,32; 13,2; 2,13; 21,3; 2,31; 23,1; 3,12; 31,2; 3,21; 32,1.