Геометрические тела и их изображение
Методический комментарий
Чтобы научиться различать геометрические тела, знать их основные свойства, учащиеся должны не только зрительно изучать их, но и иметь возможность взять изучаемое тело в руки, провести ладонью по его поверхности. Они впервые сталкиваются сразу с четырьмя типами поверхностей: сферической, цилиндрической, конической и многогранной. Для того чтобы научиться различать их, учащиеся должны руками ощутить, что у многогранников все части поверхности плоские; шар абсолютно круглый — у него нет ни одной плоской части; поверхности цилиндра и конуса более сложные — они состоят как из плоских частей, так и кривых, причём у цилиндра две плоские части, а у конуса одна, но они имеют одинаковую форму — форму круга.
Учителю необходимо позаботиться о том, чтобы учащиеся имели возможность ознакомиться как можно с большим числом различных многогранников, определить в каждом форму граней, число вершин, рёбер и граней и выявить особенности их расположения.
Для исследования формы граней многогранника необходимо использовать его сплошную модель, а для исследования рёбер удобнее — каркасную, на которой можно увидеть все рёбра тела и их расположение. Учащиеся и сами могут изготавливать модели многогранников, например из элементов конструктора или палочек, скреплённых кусочками пластилина, и т. д.
Полезно также предлагать учащимся задания на сравнение различных многогранников. Например:
1) Среди предложенных многогранников найти многогранник, у которого число вершин (рёбер, граней) наименьшее. Это треугольная пирамида.
2) Найти два разных многогранника с одинаковым числом вершин. Это могут быть параллелепипед и семиугольная пирамида.
3) Найти все многогранники, грани которых — прямоугольники.
Умение правильно воспринимать плоские изображения пространственных объектов весьма важно. Чтобы постепенно подвести учащихся к восприятию абстрактного чертежа, на котором изображаются лишь линии пересечения поверхностей (сплошными линиями — видимые, штриховыми — невидимые), на первых этапах используются прозрачные изображения тел, так как они более реальны, их нетрудно представить. Далее может быть предложена следующая практическая работа.
К доске прикрепляются вырезанные из цветной бумаги две фигуры — красный круг и зелёный треугольник (рис. 25, а).
Учащимся предлагается воспроизвести эту конфигурацию в тетради (при этом удобно использовать трафареты):
1) начертите круг;
2) сверху начертите треугольник;
3) раскрасьте треугольник;
4) раскрасьте видимую часть круга;
5) невидимую часть круга обведите штриховой линией.
Учащиеся получают изображение, показанное на рисунке 25, б. Далее на доске круг и треугольник меняются местами, и учащимся предлагается воспроизвести эту конфигурацию, но уже не используя цветные карандаши. После этого можно попросить определить по чертежу (рис. 26), какая фигура расположена сверху.
И наконец, каждый ученик может, используя имеющиеся у него трафареты, изобразить на бумаге собственную конфигурацию из двух фигур и предложить соседу по парте раскрасить фигуры в соответствии с их расположением.
Полезно научить учащихся изображать куб на клетчатой бумаге (рис. 27). Овладев этим умением, учащиеся смогут также рисовать различные многогранники, составленные из кубиков (рис. 28).
Обращаем внимание учителя на то, что если учащийся сначала изображает контур тела, а уже затем линии, лежащие внутри контура, то это значит, что он испытывает трудности в восприятии пространственных тел, не видит особенностей их строения. Такому ученику необходимо дополнительно предложить упражнения типа 926 из учебника.
В качестве дополнительных упражнений предлагается найти на рисунках в учебнике:
а) многогранник, у которого 5 граней, 5 вершин, 8 рёбер;
б) два различных многогранника, имеющих 6 вершин;
в) два различных многогранника с 5 гранями;
г) многогранник, у которого столько же граней, вершин и рёбер, сколько их у куба.
Комментарий к упражнениям
927. Для каждой грани следует использовать свой цвет.
929. Все вопросы и задания этого упражнения относятся к большему многограннику. Вернуться к этой задаче можно после рассмотрения п. 10.4, задав учащимся вопрос: «Каким многогранником является отрезанный угол куба?»
930. Обычно учащиеся выполняют это задание так: сплошные линии изображают штриховыми линиями, а штриховые — сплошными, забывая при этом, что линии контура должны оставаться сплошными. Здесь полезно отослать их к упражнению 926, в ходе выполнения которого проводился анализ того, в каких случаях грань будет иметь видимые рёбра.
931. Начать движение следует либо в вершине В, либо в вершине Е, в которых сходятся по три ребра. Закончится обход соответственно в вершине Е или в вершине В.
932. Сначала надо увидеть квадрат ABCD, а затем квадраты АKСЕ и KBED.
Параллелепипед
Методический комментарий
Каким бы простым телом ни казался нам параллелепипед, учащимся требуется определённое время на знакомство с ним. Каждый ученик должен иметь на уроке и дома какую-нибудь модель параллелепипеда. При этом важно, чтобы учащиеся не просто рассматривали параллелепипед, но и задействовали при его изучении и другие виды восприятия. Так, они должны не только глазами, но и пальцами провести по его рёбрам, ощутить, что в каждой вершине сходятся три ребра. Взяв параллелепипед в руки так, чтобы в каждой его вершине оказалось по одному пальцу, они увидят и ощутят тактильно, что число задействованных пальцев равно 8, следовательно, у параллелепипеда 8 вершин. Аналогично можно сосчитать и число его граней. Такое использование при восприятии тела различных органов чувств помогает создать более полный его мысленный образ.
Результатом подобного изучения параллелепипеда должно стать осознание целого ряда его особенностей. Все грани параллелепипеда — прямоугольники, и всего их шесть; напротив друг друга расположены равные грани, таких пар равных граней три; в каждой вершине сходятся три неравные грани. Аналогичные выводы можно сделать и о рёбрах: всего у параллелепипеда двенадцать рёбер; есть равные рёбра — три группы по четыре ребра; в каждой вершине сходятся три ребра разной длины. Наконец, вершины: их у параллелепипеда 8, по четыре вершины в каждой из противолежащих граней. Такое всестороннее и внимательное изучение параллелепипеда, однако, не предполагает, что предлагаемые далее задания выполняются учащимися в умственном плане без опоры на модели и рисунки. Так, например, при выполнении упражнения 952 из учебника можно предложить учащимся воспользоваться спичечным коробком, на котором равные рёбра обведены одним цветом (упражнение 938), а можно отослать к рисунку, на котором изображены аквариумы. Этот же спичечный коробок полезно использовать при решении других задач.
Особенностью данного пункта является комбинированный характер большинства рассматриваемых задач, который заключается не только в активной работе пространственного воображения, но и в привлечении изученных ранее понятий в новых ситуациях и сочетаниях: ломаная, составленная из рёбер куба, периметр грани, площадь поверхности и др. Это создаёт определённые сложности для учащихся, поэтому выполнение таких упражнений требует дополнительных комментариев и разъяснений учителя.
Начать работу по изучению материала, связанного с развёртками, необходимо с практической деятельности: изготовления развёртки и сворачивания её в пространственное тело. Важно при этом обращать внимание учащихся на сам процесс сворачивания, на то, какие грани оказались противоположными, а какие — соседними, какие отрезки и точки совместились. Полезно снабдить учащихся и теми фигурами, которые не могут быть развёртками, дать им возможность попытаться обнаружить это практическим путём и самостоятельно найти причину. Приобретя такой значительный опыт сворачивания развёрток, дальнейшие упражнения учащиеся смогут уже выполнять мысленно, либо вспоминая, как они сворачивали данную развёртку, если она им уже встречалась, либо по аналогии с этим, если встречаются с ней впервые. В любом случае учитель должен подстраховать тех учащихся, которым пока это сделать трудно, и снова, дав им развёртку в руки, вернуться к практическому способу решения предложенной задачи. Переход от практического решения к мысленному должен осуществляться постепенно, с учётом индивидуального развития учащихся.
Комментарий к упражнениям
948. При выполнении заданий 2—4 кубики можно использовать для проверки действий, выполненных мысленно. Однако в слабом классе эти задания полезно выполнить практически.
950. Всего кубиков 27. Одну окрашенную грань имеют кубики, расположенные в центре каждой грани большого куба; их 6. Две окрашенные грани имеют кубики, расположенные в двух гранях куба; их 4 · 6 : 2 = 12. Три окрашенные грани у кубиков, расположенных в вершинах куба; их 8. Итого окрашенных кубиков 6 + 12 + 8 = 26. Значит, один кубик останется неокрашенным; он расположен в центре куба.
954. Задание «мысленно сверните куб» может оказаться для учащихся достаточно сложным. В этом случае выполнение задания может быть организовано следующим образом. Предварительно предложить учащимся вырезать из бумаги развёртки 1 и 2. Развёртку 3 вырезать из листа ватмана.
Развёртка 1 сворачивается практически. Затем предложить учащимся, держа развёртку 2 в руках, свернуть её мысленно, после чего проверить правильность полученного решения практическим сворачиванием. Демонстрируя учащимся развёртку 3, снова предложить им мысленно свернуть развёртку, после чего свернуть её в куб. Развёртка 4 сворачивается мысленно по рисунку в учебнике. Учащимся, допустившим ошибку, предложить дома вырезать развёртку из бумаги и свернуть из неё куб.
955. Важно не только определить, какие буквы находятся на каких квадратах развёрток, но и как они расположены друг относительно друга (рис. 29).
Несколько комментариев к заданиям из рабочей тетради.
При выполнении заданий из рабочей тетради, связанных с изображением и чтением изображений, необходимо использовать модели. Модель куба надо расположить перед учащимися так, как показано на рисунке в рабочей тетради.
Чтобы представить заданный параллелепипед в ином расположении, рассуждать можно так: так как ребро LN является видимым, то видимы будут и грани LNMA, LNTC, а также грань ABCL. Рёбра этих граней обводим сплошными линиями, остальные — штриховыми.
Изображение параллелепипеда выполняется от руки.
Объём параллелепипеда
Методический комментарий
Начать изучение пункта «Объём параллелепипеда» полезно с напоминания о том, как измеряют длины и площади (выбор единицы измерения и др.).
Вывод правила вычисления объёма параллелепипеда аналогичен выводу правила вычисления площади прямоугольника, поэтому сначала полезно повторить вывод этого правила. Заметим, что очень важно сопроводить вывод правила нахождения объёма параллелепипеда практическим выполнением учащимися описанных в учебнике действий. Полезно дать каждому учащемуся возможность повторить эти действия самостоятельно, проговаривая и поясняя их. Эти действия по заполнению пространства кубиками следует постепенно перевести в умственный план. Необходимость в них со временем отпадёт и, сохраняя идею измерения пространства, учащиеся смогут сначала перейти к правилу вычисления объёма параллелепипеда, а позднее и к формуле. Этим и определяется значительная доля заданий с кубиками, в которых требуется изобразить тело заданного объёма, сложить (мысленно или практически) параллелепипед и определить его измерения, по изображению определить число кубиков, вошедших в коробку, и т. д. Кроме того, эти упражнения прекрасно развивают пространственное воображение: умение представить фигуру по её описанию или изображению, выполнить с ней заданные действия.
Учащиеся должны уметь приблизительно представлять 1 см3, 1 дм3, 1 м3, знать, что 1 дм3 = 1 л, представлять объёмы некоторых сосудов (например, объём стакана равен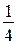 
л = 250 мл = 250 см3, объём ведра равен приблизительно 10 л, объём чайной ложки — 5 см3, или 5 мл).
Перевод одних единиц в другие должен опираться на знание линейных метрических зависимостей. Полезно, если учащиеся сами составят табличку зависимостей между основными единицами объёма и будут пользоваться ею в дальнейшем при выполнении упражнений.
Комментарий к упражнениям
971. Полезно обсудить два варианта решения задачи: 1) вычислить объёмы, заполненные водой; 2) вычислить объёмы, оставшиеся незаполненными.
973. Здесь нужно мысленно укладывать пакеты в коробку, а вычислив необходимые объёмы, можно оценить результат.
Пирамида
Методический комментарий
Пирамида — один из самых важных и интересных многогранников.
И учащиеся этого возраста должны уметь её распознавать на моделях и графических изображениях. Методика изучения пирамиды аналогична методике, предложенной для изучения параллелепипеда.
Обращаем внимание учителя на то, что здесь не подразумевается вывод зависимости числа вершин и рёбер n-угольной пирамиды от числа n вершин основания. Но в результате изучения, анализа различных пирамид у учащихся должно сложиться подкреплённое зрительными образами понимание того, что число вершин пирамиды на единицу больше числа вершин в её основании, рёбер боковых граней столько же, сколько их в основании, число боковых граней равно числу сторон основания, все боковые грани сходятся к вершине, противолежащей основанию, а следовательно, само название пирамиды помогает узнать, сколько у неё вершин, рёбер и граней.
Комментарий к упражнениям
987. Задание выполняется с пирамидой в руках.
993. Многогранник можно вылепить из пластилина и разрезать его.
994. 2) См. рисунок 30.
В рабочей тетради есть задание о перекатывании пирамиды с одной грани на другую. Необходимо предусмотреть возможность практического решения. Учащиеся должны подметить закономерность: третьей будет вершина, отсутствующая в предыдущем треугольнике. Ребро BD общее для граней BCD и BDA, значит, первая непроставленная вершина — вершина А, затем последовательно вершины С и В.
Глава 11. Таблицы и диаграммы (9 уроков)
Примерное поурочное планирование учебного материала
| Пункт учебника | Число уроков | Рабочая тетрадь, номер задания, с. 63—78 | Характеристика деятельности учащихся |
| 11.1. Чтение и составление таблиц | 9—12 (ч. 2) | Знакомитьсясразличными видами таблиц.Анализировать готовые таблицы, извлекатьиз нихинформацию; сравнивать между собой представленные в таблицах данные из реальной практики; выполнять вычисления по табличным данным. Заполнять простые таблицы, следуя инструкции | |
| 11.2. Диаграммы | 13—15 (ч. 2) | Знакомитьсяс такими видами диаграмм, как столбчатые и круговые диаграммы. Анализировать готовые диаграммы; сравнивать между собой представленные на диаграммах данные, характеризующие некоторое реальное явление или процесс, выполнять вычисления по данным диаграммы. Строить в несложных случаях простые столбчатые диаграммы, следуя образцу | |
| 11.3. Опрос общественного мнения | 16—17 (ч. 2) | Знакомитьсяс примерами опроса общественного мнения и простейшими способами представления данных. Проводитьнесложныеисследования общественного мнения, связанные с жизнью школы, внешкольными занятиями и увлечениями одноклассников: формулировать вопросы, выполнять сбор информации, представлять её в виде таблицы и столбчатой диаграммы | |
| Обзор | Анализироватьданные опросов общественного мнения, представленные в таблицах и на диаграммах, строить столбчатые диаграммы |
Основные цели: сформировать умения извлекать необходимую информацию из несложных таблиц и столбчатых диаграмм.
Обзор главы. Здесь начинается формирование умения работать с информацией, представленной в форме таблиц и диаграмм, которые широко используются в средствах массовой информации, справочной литературе и т. д. Наряду с этим у учащихся формируются первоначальные представления о приёмах сбора необходимых данных, предъявлении этих данных в компактной табличной форме и наглядном изображении в форме столбчатой диаграммы. На примере опроса общественного мнения учащиеся знакомятся с основными этапами проведения социологических опросов. Однако главным при этом является формирование умения анализировать готовые таблицы и диаграммы и делать соответствующие выводы.
Чтение и составление таблиц
Методический комментарий
Объяснение материала начинается с рассмотрения знакомой учащимся страницы классного журнала с отметками по математике за октябрь. Информация об отметках представлена в виде таблицы с двумя входами — фамилии учащихся и даты учебных занятий за месяц. Вводятся термины, связанные с использованием табличной формы представления данных: строка, столбец. В процессе выполнения упражнений у учащихся формируется умение извлекать информацию, заключённую в клетке таблицы, в строке, в столбце, в части строки или части столбца. Кроме того, школьники учатся анализировать табличную информацию и делать на этой основе соответствующие выводы.
При рассмотрении несложных жизненных ситуаций учащиеся знакомятся с приёмами составления таблиц и условными обозначениями, которые принято использовать при их построении.
Объяснение начинается с рассмотрения так называемой частотной таблицы, но сам термин не вводится (пример 1 из объяснительного текста учебника).
В ходе выполнения упражнений учащиеся познакомятся с частотной таблицей, в которой значения величины записаны в виде числового интервала (упражнение 1003). Учащиеся узнают о том, что такие таблицы позволяют экономно представить информацию, когда рассматриваемая величина имеет много значений.
При рассмотрении таблицы с результатами шахматного турнира (пример 2 из объяснительного текста) учащиеся получают представление об общих приёмах составления турнирных таблиц, а также о принятой в шахматах системе присвоения баллов участникам игры и приёмах записи результатов игр в клетки таблицы.
Формирование умения строить частотные или турнирные таблицы не является обязательной учебной целью. Главное — это показать учащимся, как заполняются клетки таблицы, и тем самым облегчить понимание информации, представленной в готовых таблицах.
Выполняя упражнения, учащиеся знакомятся также с так называемыми пиктограммами (от английского слова picture — картина), в которых для обозначения численности предметов используются различные картинки
(см. таблицу в упражнении 1004). Эти картинки могут быть связаны по смыслу с изображаемой ими информацией, как это сделано, например, в задании 2 рубрики «Чему вы научились».
Комментарий к упражнениям
1002. При выполнении этого упражнения рассматривается один из приёмов, позволяющих увеличить объём информации, представленной в таблице: формирование итоговой строки, в которой суммируются данные по каждому из столбцов таблицы, и итогового столбца, в котором суммируются данные по каждой из строк. Учащиеся убеждаются в том, что сумма данных итоговой строки такая же, как сумма данных итогового столбца. Целесообразно обратить внимание учащихся на то, что сравнение этих сумм позволит проверить правильность заполнения итоговой строки и итогового столбца конкретной таблицы.