Нахождение части целого и целого по его части

Методический комментарий

Овладение способами решения задач указанного вида является одной из важнейших целей изучаемой темы. Здесь рассматриваются два способа решения таких задач — на основе смысла понятия дроби и с помощью формальных правил (умножение и деление на дробь). Заметим, что на этом этапе второй способ можно вообще не рассматривать, ограничившись лишь решением задач на содержательной основе. Дело в том, что в начале 6 класса в теме «Обыкновенные дроби» учащиеся ещё раз возвращаются к решению задач указанных видов, и второй, более формальный способ решения таких задач может быть рассмотрен в следующем проходе. Однако и в том случае, если будут рассмотрены оба способа, учащийся каждый раз вправе решать, каким способом ему удобнее получить ответ. Подчеркнём, что решение практически всех задач должно сопровождаться рисунком, и более того, рисунок может составлять основу решения задачи.

Комментарий к упражнениям

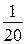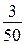883.б) Возможно такое решение: дроби и приводятся к знаменателю 100, а потом находят 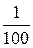от числа страниц и этот результат умножают на 5, 6, 3.

885. Рекомендуем решать задачу прямым вычислением расстояний: сначала пройденного в первый день, потом во второй день и затем в третий день.

Но после решения следующей задачи 886 советуем вернуться к данной и записать другое её возможное решение:

1) 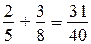— такую часть пути проехали за два дня;

2) 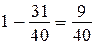— такую часть пути проехали за 3-й день;

3) 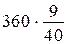= 81 (км) — столько проехали за 3-й день.

887.Ещё раз обращаем внимание учителя на то, что решение этой и последующих задач должно сопровождаться рисунком.

894.а) Выясните, какую часть книги занимает первая повесть, и решите задачу на нахождение целого по его части. Понимание идеи решения задач этого упражнения поможет освоению способа решения задачи, разобранной в следующем упражнении.

Задачи на совместную работу

Методический комментарий

В ходе изучения материала учащиеся осваивают новый для них, довольно трудный тип задач. В обязательные результаты обучения подобные задачи не входят. Тем не менее желательно организовать работу так, чтобы школьники сами «открыли» способ решения таких задач. Для этого уже есть предпосылки — при изучении предыдущих тем учащиеся решали задачи, являвшиеся отдельными элементами задач на совместную работу (упражнения 760, 766—768, 818, 839). Так, в задаче 760 при условии «Рабочий может выполнить заказ за 3 ч, а ученик — за 7 ч» требуется ответить на вопросы: «Какую часть заказа выполнит рабочий за 1 ч? Какую часть заказа выполнит ученик за 1 ч? Какую часть заказа они выполнят, работая вместе, за 1 ч?» Кроме того, в учебном тексте найдено методическое решение, помогающее учащимся понять идею решения задач на совместную работу.

Здесь также продолжается решение задач на движение, которое подготовлено рассмотренными ранее задачами.

Комментарий к упражнениям

907. а) План решения задачи может быть следующим:

1) Какую часть материалов расходуют в день оба цеха, работая вместе?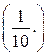

2) Какую часть материалов расходует в день первый цех?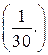

3) Какую часть материалов расходует в день второй цех?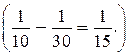

4) За сколько дней израсходует материалы второй цех, если будет работать один? (За 15 дней.)

908. Первая бригада выполняет в день 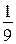задания, за 3 дня она выполнила 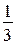задания. Второй бригаде осталось выполнить 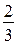задания. Она выполняет в день 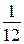задания, поэтому закончит работу за 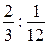= 8 дней. Вся работа будет выполнена за 3 + 8 = 11 дней.

912. Решение.

1) 1 : 6 = 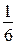— такую часть расстояния проплывает катер за 1 ч по озеру;

2) 1 : 5 = 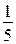— такую часть расстояния проплывает катер за 1 ч по течению реки;

3) 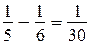— на такую часть расстояния сносится течением катер, а значит, и плот за 1 ч;

4) 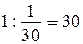(ч) — столько времени потребуется плоту.

913. Решение.

Плот плывёт от А до В, значит, катер при этом движется по течению реки, а от В до А — против течения.

1) 1 : 40 = 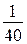— такую часть расстояния проплывает плот за 1 ч по течению реки;

2) 1 : 4 = 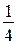— такую часть расстояния проплывает катер за 1 ч по течению реки;

3) 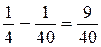— такую часть расстояния проплывает катер за 1 ч в стоячей воде;

4) 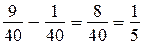— такую часть расстояния проплывает катер за 1 ч против течения;

5) 1 : 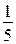= 5 (ч) — такое время затратит катер на путь от В до А.

914. Стандартная ошибка, которую допускают учащиеся при решении этой задачи: действием 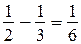они «находят» скорость течения (часть расстояния, на которую река относит за 1 ч лодку, плот, бревно и т. п.). Между тем, чтобы найти скорость течения, надо результат этого действия ещё разделить на 2.

915. а) За 30 ч слон выпьет 10 озёр, слониха — 6 озёр и слонёнок —
5 озёр, т. е. все вместе они выпьют 10 + 6 + 5 = 21 озеро. Значит, одно озеро они выпьют за 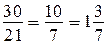ч.

б) Лошадь съедает воз сена за месяц, значит, за год она съедает 12 возов сена. Коза, которая съедает воз сена за два месяца, за год съедает 6 возов сена. А овца, которая съедает воз сена за три месяца, за год съест 4 воза сена. Значит, вместе они за год (т. е. за 12 месяцев) съедят 12 + 6 + 4 = 22 воза сена. Поэтому воз сена они съедят за 12 : 22 = 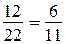месяца.

Глава 10. Многогранники (10 уроков)

Примерное поурочное планирование учебного материала

Пункт учебника	Число уроков	Рабочая тетрадь, номер задания	Характеристика деятельности учащихся
10. 1. Геометрические тела и их изображение		106—119 (ч. 2)	Распознаватьна чертежах, рисунках, в окружающем мире многогранники. Читатьпроекционные изображения пространственных тел: распознавать видимые и невидимые рёбра, грани, вершины. Копироватьмногогранники, изображённые на клетчатой бумаге,осуществлять самоконтроль, проверяя соответствие полученного изображения заданному. Моделироватьмногогранники, используя бумагу, пластилин, проволоку и т. д. Исследоватьсвойства многогранников, используя эксперимент, наблюдение, измерение, моделирование. Описыватьих свойства, используя соответствующую терминологию.Сравниватьмногогранники по числу и взаимному расположению граней, рёбер, вершин
10.2. Параллелепипед		120—130, 136—140 (ч. 2)	Распознавать на чертежах, рисунках, в окружающем мире параллелепипед и пирамиду. Называть пирамиды. Копировать параллелепипеды и пирамиды, изображённые на клетчатой бумаге, осуществлять самоконтроль, проверяя соответствие полученного изображения заданному. Моделировать, используя бумагу, пластилин, проволоку и т. д. Определятьвзаимное расположение граней, рёбер, вершин параллелепипеда. Находить измерения параллелепипеда. Исследоватьсвойства параллелепипеда и пирамиды, используя эксперимент, наблюдение, измерение, моделирование. Описывать их свойства, используя соответствующую терминологию. Формулироватьутверждения о свойствах параллелепипеда, пирамиды, опровергать утверждения с помощью контрпримеров
10.3. Объём параллелепипеда		—	Моделироватьпараллелепипеды из единичных кубов, подсчитывать число кубов.Вычислятьобъёмы параллелепипедов, кубов по соответствующим правилам и формулам. Моделировать единицы измерения объёма. Выражатьодни единицы измерения объёма через другие.Выбиратьединицы измерения объёма в зависимости от ситуации.Выполнять практико-ориентированные задания на нахождение объёмов объектов, имеющих форму параллелепипеда. Решатьзадачи на нахождение объёмов параллелепипедов.Вычислятьобъёмы многогранников, составленных из параллелепипедов
10.4. Пирамида		131—135, 141—142 (ч. 2)	Распознаватьразвёртки куба, параллелепипеда, пирамиды. Изображатьразвёртки куба на клетчатой бумаге. Моделироватьпараллелепипед, пирамиду из развёрток. Исследоватьразвёртки куба, особенности расположения отдельных её частей,используя эксперимент, наблюдение, измерение, моделирование. Описыватьих свойства
Обзор и контроль		Распознавать на чертежах, рисунках, в окружающем мире многогранники. Выделятьвидимые и невидимые грани, рёбра. Изображатьих на клетчатой бумаге, моделировать, используя бумагу, пластилин, проволоку и т. д. Характеризоватьвзаимное расположение и число элементов многогранников по их изображению. Исследоватьмногогранники, используя эксперимент, наблюдение, измерение, моделирование. Описыватьих свойства. Вычислятьобъёмы параллелепипедов, использовать единицы измерения объёма. Решатьзадачи на нахождение объёмов параллелепипедов

Основные цели:познакомить учащихся с такими телами, как цилиндр, конус, шар; сформировать представление о многограннике; познакомить со способами изображения пространственных тел, в том числе научить распознавать многогранники и их элементы по проекционному чертежу; научить изображать параллелепипед и пирамиду; познакомить с понятием объёма, единицами объёма и правилом вычисления объёма прямоугольного параллелепипеда.

Обзор главы. В данной главе учащиеся знакомятся с такими геометрическими телами, как цилиндр, конус и шар, объектом же более детального исследования являются многогранники.

Важнейшей целью изучения данного раздела является развитие пространственного воображения учащихся. В ходе выполнения заданий необходимо учить их осуществлять несложные преобразования созданного образа, связанные с изменением его пространственного положения или конструктивных особенностей (например, мысленно свернуть куб из развёртки).

Учащиеся знакомятся со способами изображения геометрических тел на листе бумаги (рисунок сплошной или прозрачной модели, проекционный чертёж) и учатся «читать» эти изображения, отмечая основные конструктивные особенности геометрического тела: число вершин, рёбер, граней, их расположение.

Более подробно учащиеся изучают такие многогранники, как параллелепипед и пирамида. Они учатся распознавать их на сплошных и каркасных моделях и по графическим изображениям, изображать на клетчатой бумаге, узнавать основные конструктивные особенности: число вершин, граней и рёбер, форму граней, число рёбер, сходящихся в вершинах, и т. д.

Линия измерения геометрических величин продолжается темой «Объём параллелепипеда», изложение которой построено по такому же плану, как и тема «Площадь прямоугольника»:

1) выбор единиц объёмов;

2) объём параллелепипеда есть число составляющих его единичных кубов;

3) вывод правила вычисления объёма параллелепипеда.

Материалы для контроля.

Пособие «Контрольные работы». Проверочные работы:
7. Многогранники. 8. Прямоугольный параллелепипед. 9. Объём.
10. Пирамида.