Глава 7. Треугольники и четырёхугольники

(10 уроков)

Примерное поурочное планирование учебного материала

Пункт учебника	Число уроков	Рабочая тетрадь, номер задания	Характеристика деятельности учащихся
7.1. Треугольники и их виды		74—81 (ч. 2)	Распознавать треугольники на чертежах и рисунках, приводить примеры аналогов этих фигур в окружающем мире. Изображатьтреугольники от руки и с использованием чертёжных инструментов, на нелинованной и клетчатой бумаге; моделировать, используя бумагу, проволоку и т. д. Исследовать свойства треугольников путём эксперимента, наблюдения, измерения, моделирования, в том числе с использованием компьютерных программ. Измерятьдлины сторон, величины углов треугольников. Классифицировать треугольники по углам, по сторонам. Распознаватьравнобедренные и равносторонние треугольники. Использовать терминологию,связанную с треугольниками. Выдвигать гипотезы о свойствах равнобедренных, равносторонних треугольников, обосновывать их. Объяснять на примерах, опровергать с помощью контрпримеров утверждения о свойствах треугольников. Находитьпериметр треугольников, в том числе выполняя необходимые измерения. Конструироватьорнаменты и паркеты, изображая их от руки, с помощью инструментов
7.2. Прямоугольники		82—86 (ч. 2)	Распознавать прямоугольники на чертежах и рисунках, приводить примеры аналогов прямоугольников в окружающем мире. Формулироватьопределения прямоугольника, квадрата. Изображатьпрямоугольники от руки на нелинованной и клетчатой бумаге, строить, используя чертёжные инструменты, по заданным длинам сторон; моделировать, используя бумагу, проволоку и т. д. Находить периметр прямоугольников, в том числе выполняя необходимые измерения. Исследоватьсвойства прямоугольников путём эксперимента, наблюдения, измерения, моделирования. Сравниватьсвойства квадрата и прямоугольника общего вида. Выдвигать гипотезыо свойствах прямоугольника, обосновывать их. Объяснять на примерах, опровергать с помощью контрпримеров утверждения о свойствах прямоугольников
7.3. Равенство фигур		87—91 (ч. 2)	Распознавать равные фигуры, проверять равенство фигур наложением. Изображатьравные фигуры. Разбиватьфигуры на равные части, складывать из равных частей. Обосновывать, объяснять на примерах, опровергать с помощью контрпримеров утверждения о равенстве фигур. Формулировать признаки равенства отрезков, углов, прямоугольников, окружностей. Конструировать орнаменты и паркеты, изображая их от руки, с помощью инструментов
7.4. Площадь прямоугольника		92—105 (ч. 2)	Вычислять площади квадратов, прямоугольников по соответствующим правилам и формулам. Моделироватьфигуры заданной площади, фигуры, равные по площади. Моделировать единицы измерения площади. Выражать одни единицы измерения площади через другие. Выбирать единицы измерения площади в зависимости от ситуации. Выполнять практико-ориентированные задания на нахождение площадей. Вычислять площади фигур, составленных из прямоугольников. Находитьприближённое значение площади фигур, разбивая их на единичные квадраты. Сравнивать фигуры по площади и периметру. Решатьзадачи на нахождение периметров и площадей квадратов и прямоугольников. Выделять в условии задачи данные, необходимые для её решения, строить логическую цепочку рассуждений, сопоставлять полученный результат с условием задачи
Обзор и контроль		Распознаватьтреугольники, прямоугольники на чертежах и рисунках, определять вид треугольников. Изображать треугольники, прямоугольники с помощью инструментов и от руки. Находитьпериметр треугольников, прямоугольников. Вычислять площади квадратов и прямоугольников. Решать задачи на нахождение периметров и площадей квадратов и прямоугольников. Исследовать свойства треугольников, прямоугольников путём эксперимента, наблюдения, измерения, моделирования, в том числе с использованием компьютерных программ. Формулировать утверждения о свойствах треугольников, прямоугольников, равных фигур. Обосновывать, объяснять на примерах, опровергать с помощью контрпримеров утверждения о свойствах треугольников, прямоугольников, равных фигур. Конструировать алгоритм воспроизведения рисунков, построенных из треугольников, прямоугольников, строить по алгоритму, осуществлять самоконтроль, проверяя соответствие полученного изображения заданному рисунку. Конструировать орнаменты и паркеты с помощью инструментов и от руки

Основные цели: познакомить учащихся с классификацией треугольников по сторонам и углам; развить представления о прямоугольнике; сформировать понятие равных фигур, площади фигуры, научить находить площади прямоугольников и фигур, составленных из прямоугольников; познакомить с единицами измерения площадей.

Обзор главы. В этой главе учащиеся углубляют свои знания о треугольниках и четырёхугольниках: они знакомятся с классификациями треугольников по сторонам и углам, со свойствами равнобедренного треугольника, а также со свойствами прямоугольника.

Здесь же вводится понятие равных фигур. Заметим, что у учащихся уже есть интуитивное представление о равных фигурах. Оно сформировалось в ходе выполнения таких заданий, как вырезание фигур из бумаги, перечерчивание фигуры по клеткам квадратной сетки и т. д. При этом речь шла о построении «такой же фигуры, как данная», о вырезании одинаковых фигур. Теперь интуитивные представления учащихся обобщаются и систематизируются. Вводится термин «равные фигуры» и разъясняется, что так называют фигуры, которые могут быть совмещены друг с другом путём наложения. Это понятие конкретизируется по отношению к уже известным фигурам: отрезкам, углам, окружностям и т. д.

Линия измерения геометрических величин продолжается темой «Площадь фигуры». Из начальной школы учащимся известно, как найти площадь прямоугольника. Здесь эти знания актуализируются, отрабатываются и расширяются: формируется представление о площади фигуры как о числе единичных квадратов, составляющих данную фигуру; о свойстве аддитивности площади (без соответствующей терминологии); правило вычисления площади квадрата формулируется через понятие «квадрат числа»; вводятся новые единицы площади (гектар, ар); выявляются зависимости между единицами площади, объясняется, как можно приближённо вычислить площадь круга.

Материалы для контроля.

Пособие «Контрольные работы». Проверочные работы: 4. Треугольники. 5. Прямоугольники. 6. Площади.

Треугольники и их виды

Методический комментарий

Содержание данного пункта является, с одной стороны, совершенно новым для учащихся, с другой стороны, весьма значимым с точки зрения геометрии. Оно включает классификацию треугольников по сторонам и углам, а также понятие равнобедренного треугольника (определение, свойство углов при основании). Основным результатом изучения данного пункта следует считать умение распознать и изобразить прямоугольный, остроугольный, тупоугольный, равнобедренный треугольники; знание терминологии, связанной с равнобедренным треугольником.

В процессе практической деятельности учащиеся должны понять: в треугольнике не может быть больше одного прямого или одного тупого угла, равнобедренный треугольник может быть и прямоугольным, и остроугольным, и тупоугольным, а вот равносторонний треугольник только остроугольным.

Комментарий к упражнениям

528. б) Найдём длину третьей стороны треугольника. Она равна
17 – (5 + 6) = 6 см. Этот треугольник является равнобедренным, так как длины его сторон равны 5 см, 6 см и 6 см.

Прямоугольники

Методический комментарий

Прямоугольник является для учащихся, пожалуй, самой известной фигурой. Однако из-за недостаточной геометрической подготовки учащихся в начальной школе многие из них воспринимают его как единую фигуру и не видят составляющие его элементы. По этой причине квадрат и прямоугольник для них две различные фигуры, две различные формы: квадратная и прямоугольная. Восполнить этот пробел не удастся, лишь сообщив учащимся, что квадрат тоже прямоугольник. К этой мысли они должны привыкнуть при выполнении упражнений: учащиеся смогут понять, что если некоторое свойство имеет место для прямоугольника общего вида, то оно имеет место и для квадрата, а вот обратное неверно: то, что выполняется для квадрата, может и не выполняться для прямоугольника общего вида. Естественно, что эту мысль должен (и неоднократно) произнести учитель, а учащиеся на этом этапе слушают и осознают.

Учащиеся должны научиться изображать квадрат и прямоугольник с заданными сторонами на клетчатой и нелинованной бумаге от руки и с использованием инструментов, моделировать их из бумаги.

В тексте пункта построение прямоугольника описано таким образом, что каждый выделенный шаг предложенного алгоритма иллюстрируется отдельным рисунком. Таким образом, каждый следующий рисунок содержит в себе предыдущий и построения нового шага. Это позволяет сделать отдельные этапы построения более наглядными, а сопоставление текста и визуальной информации способствует более чёткому выделению этапов построения, их осмыслению и запоминанию.

В качестве дополнительного задания здесь можно предложить учащимся найти другой вариант предложенного алгоритма (построить угол D прямоугольника), обсудить, какие измерения нужно провести в каждом случае для проверки точности и аккуратности выполненных действий (равны ли длины противолежащих сторон, все ли углы прямые).

Новые для учащихся свойства прямоугольника связаны в основном с его диагоналями. В этом пункте они узнают, что диагонали прямоугольника равны и в точке пересечения делятся пополам. В следующем пункте, где речь идёт о равенстве фигур, им предстоит узнать, что диагональ делит прямоугольник на два равных прямоугольных треугольника, а две диагонали — на две пары равных равнобедренных треугольников.

Дополнительное задание. Периметр прямоугольника равен 18 см. Одна сторона больше другой на 1 см. Начертите в тетради такой прямоугольник.

Равенство фигур

Методический комментарий

Интуитивное понимание учащимися равенства как одинаковости, идентичности использовалось нами при различных видах копирования геометрических фигур. Здесь это интуитивное представление осмысливается и формулируется в виде определения понятия равенства. Оговоримся сразу, что знания этой формулировки от учащихся не требуется. Признаки равенства тоже неоднократно употреблялись ранее на интуитивном уровне: ведь сколько бы отрезков длиной, например, 5 см учащийся ни начертил, все они будут одинаковыми, ничем не отличающимися друг от друга.

Одна из задач пункта — научить учащихся находить в равных фигурах соответственно равные элементы, а также записывать необходимые равенства.

Помимо этого, учащиеся должны увидеть и запомнить, что диаметр разбивает круг на два равных полукруга; диагональ разбивает прямоугольник на два равных треугольника.

Заметим, что в ходе изучения этой темы опосредованно формируется чрезвычайно важное умение — делить фигуру на равные доли. Это умение, а также соответствующие образы составляют наглядную опору для изучения обыкновенных дробей. Учащиеся должны научиться делить на равные части, в том числе и без инструментов, отрезок, прямоугольник, квадрат, круг. Они должны также получить представление о возможности удвоения числа равных долей: разделить фигуру пополам, ещё раз пополам и т. д.

Дополнительные вопросы и задания

1) Начертите какой-нибудь отрезок. Разделите его от руки на 2, 4, 8 равных частей.

2) Начертите какой-нибудь угол. Проведите на глаз биссектрису угла. Проведите биссектрисы каждого из получившихся углов. На сколько равных частей вы разделили исходный угол?

3) Начертите круг. Разделите его на 2, 4, 8 равных частей. Сколько диаметров вы провели? Сколько диаметров нужно провести, чтобы разбить круг на 16 равных частей? на 32 равные части?

4) Начертите квадрат и разделите его на 8 равных частей разными способами.

5) Начертите прямоугольник и разделите его на 16 равных частей.

Комментарий к упражнениям

559. 2) Из получившихся треугольников можно сложить два различных равнобедренных треугольника. Полезно предложить учащимся изобразить эти треугольники в тетради.

3) Задача, обратная предыдущей задаче. В случае затруднений учащиеся могут воспользоваться треугольниками, рассмотренными в этой задаче.

560.Прежде чем работать с изображением круга в тетради, можно предложить учащимся вырезать круг из листа бумаги и сложить его пополам. Учащиеся увидят, что отрезок, делящий круг на две равные части, должен проходить через центр круга, т. е. это диаметр круга. Ещё раз перегнув круг пополам, учащиеся наглядно увидят, что радиусы «четвертинок» круга образуют прямой угол.

562. а) Задача аналогична составлению фигур из четырёх равных квадратов. Многоугольники изображены на рисунке 22.

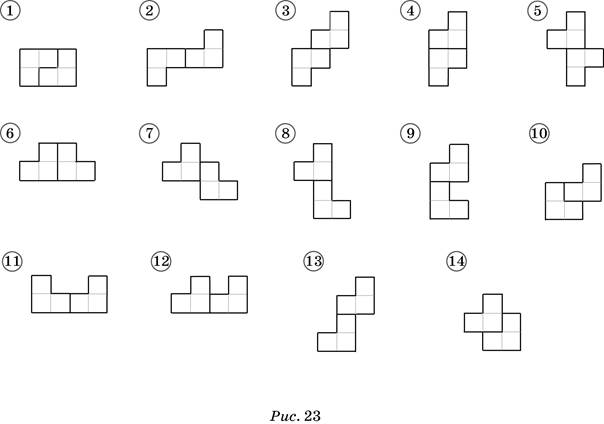
б) Фигуры изображены на рисунке 23.

566. Если учащиеся не знают, что круг составляет 360°, то сначала можно выполнить задание «б» — разделить круг на 6 равных частей. Для этого круг делится пополам, а затем каждый полукруг на 3 равные части.

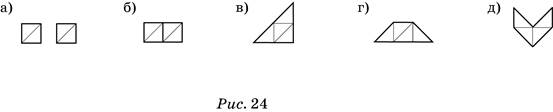
567. Фигуры изображены на рисунке 24.

Площадь прямоугольника

Методический комментарий

Несмотря на то что понятие «площадь фигуры » и правило вычисления площади прямоугольника известны учащимся из начальной школы, говорить о сформированности этого сложного понятия преждевременно. Поэтому целесообразно снова вернуться к рассмотрению этого вопроса. Новым для учащихся будет то, что первоначально площадь находится в абстрактных единицах — вводятся понятия «единица длины» и «квадратная единица». Сначала фигуры разбиты на квадраты, площади которых приняты за 1 кв. ед., затем осуществляется переход к конкретным метрическим единицам длины и площади. Поначалу можно записывать метрические единицы площади по аналогии с записью 1 кв. ед.: 1 кв. см, 1 кв. м и т. д., а лишь потом перейти к использованию степенной формы записи (см², м²).

Подчеркнём, что учащимся требуется определённое время, чтобы перейти от нахождения площади прямоугольника путём разбиения на единичные квадраты к формальному правилу. Не следует торопить их, иначе это правило может быть усвоено в отрыве от понятия площади фигуры и практическое применение его будет затруднено. Поэтому начать лучше с практического разбиения прямоугольника на соответствующие квадратные единицы (выбор единиц также необходимо обсудить). Например, чтобы найти площадь квадрата со стороной 12 см, учащиеся должны начертить такой квадрат в тетради, разбить его на квадраты со стороной 1 см, закрасить один из квадратов площадью 1 кв. см, а затем подсчитать число таких квадратов. Если учащиеся самостоятельно справляются с подобными заданиями, тогда можно переходить к применению правила.

С единицами площади учащиеся знакомятся уже в начальной школе, но, несмотря на это, многие не имеют о них реальных, наглядных представлений: не могут выбрать единицу площади в конкретном случае, затрудняются оценить на глаз площадь фигуры и т. д. Поэтому прежде всего они должны начертить на листе миллиметровой бумаги 1 мм², 1 см², 1 дм², на доске или на земле 1 м² и попытаться их запомнить. Затем полезно оценить площади, например, классной комнаты, окна, доски, тетрадного листа и т. д., мысленно сравнивая их с этими эталонами. Проведя практические измерения или просто прикинув линейные размеры, можно сравнить, например, площадь класса или спортивной площадки с соткой, а площадь школьного участка с гектаром. Здесь также целесообразно предложить каждому ученику практическую работу по нахождению площади своей комнаты.

Предполагается, что при решении задач, содержащих различные единицы площади, учащиеся опираются лишь на знание соотношений между линейными единицами. Запоминание соотношений между квадратными единицами не является обязательным. Рассуждение может быть, например, таким: 1 дм = 10 см, поэтому 1 дм² = 10 · 10 = 100 см², а 7 дм² = 700 см².

Отметим, что к некоторым заданиям данного раздела полезно вернуться при изучении обыкновенных дробей. Так, например, можно задать следующие вопросы: «Чему равны площади фигур, изображённых на рисунке 7.30, если за 1 кв. ед. принять площадь фигуры 3?», «Фигуру
(рис. 7.32) разделили на два прямоугольника. Какую часть от площади многоугольника составляет площадь каждого прямоугольника?».

Комментарий к упражнениям

578. Эта задача является обратной задаче нахождения площади прямоугольника по его сторонам и как всякая обратная задача может вызвать затруднения у некоторых учащихся. В этом случае можно переформулировать задачу, уйдя от её геометрического содержания, так: «Произведение двух чисел равно 600, один из множителей — 30. Как найти другой множитель?» Акцент на такие задачи будет сделан в 6 классе при работе с формулами, и здесь они не должны отрабатываться.

580. а) Рассуждаем так: 1 м² — это площадь квадрата со стороной 1 м, в одном метре содержится 100 см, значит, в одном квадратном метре содержится 100 · 100 = 10 000 см², а в 4 м² — 40 000 см².

591. Задача решается практически. Надо предложить учащимся начертить в тетради произвольный прямоугольник (квадрат). Уменьшить (увеличить) сторону прямоугольника (квадрата) в 3 раза (вдвое) и начертить новый прямоугольник (квадрат). Легко видеть, что площадь исходного прямоугольника (квадрата) в 3 (4) раза больше (меньше) площади получившегося.

594. Сумма длин смежных сторон данного прямоугольника равна 8 см. Это могут быть прямоугольники со сторонами 1 см и 7 см, 2 см и 6 см, 3 см и 5 см, 4 см и 4 см. Площади этих прямоугольников соответственно равны 7 см², 12 см², 15 см² и 16 см². Значит, дины сторон искомого прямоугольника равны 3 см и 5 см.

596. Сначала найдём сторону квадрата, площадь которого равна
4а = 400 м². Она равна 20 м. (Это число находится подбором.) Теперь изобразим этот квадрат в тетради, считая сторону клетки за 2 м. Получим квадрат со стороной 10 клеток. Будем «высаживать яблони» вдоль одной из сторон квадрата, от руки изображая окружности радиусом, равным стороне одной клетки. Понятно, что мы высадили 5 яблонь. Число таких рядов также равно 5, а значит, на этом участке можно высадить 5 · 5 = 25 яблонь.

598. 1) Полезно наглядно показать учащимся, что площадь цветного квадрата равна половине площади всего квадрата. Для этого надо вырезать квадрат из листа бумаги и загнуть белые треугольники к центру, наложив их на цветные. Мы получим два равных квадрата — белый и цветной.

Глава 8. Дроби (18 уроков)

Примерное поурочное планирование учебного материала

Пункт учебника	Число уроков	Рабочая тетрадь, номер задания	Дидактические материалы	Характеристика деятельности учащихся
8.1. Доли		—		Моделировать в графической, предметной форме доли и дроби.Решать текстовые задачи с опорой на смысл понятия доли
8.2. Что такое дробь		83—98 (ч. 1)	О-25, П-20, П-21, «Проверь себя»	Оперировать с математическими символами: записывать доли в виде обыкновенной дроби, читатьдроби.Называть числитель и знаменатель обыкновенной дроби, объяснять их содержательный смысл. Отмечать дроби точками координатной прямой, определять координаты точек, отмеченных на координатной прямой. Решать текстовые задачи с опорой на смысл понятия дроби. Применять дроби для выражения единиц измерения длины, массы, времени в более крупных единицах
8.3. Основное свойство дроби		99—110 (ч. 1)	О-26, П-22	Формулироватьосновное свойство дроби и записывать его с помощью букв. Моделировать в графической форме и с помощью координатной прямой отношение равенства дробей. Применять основное свойство дроби к преобразованию дробей. Находить ошибки при сокращении дробей или приведении их к новому знаменателю и объяснять их. Анализировать и формулировать закономерности, связанные с обыкновенными дробями. Применять дроби и основное свойство дроби при выражении единиц измерения величин в более крупных единицах. Применятьпризнаки делимости для сокращения дробей. Доказывать возможность сокращения дроби с опорой на признаки делимости
8.4. Приведение дробей к общему знаменателю		(ч. 1)	О-27, П-23	Применять рассмотренные алгоритмы приведения дробей к наименьшему общему знаменателю; распознавать случаи, в которых применяется тот или иной из разобранных алгоритмов
8.5. Сравнение дробей		112—116 (ч. 1)	О-28, П-24, «Проверь себя»	Моделировать с помощью координатной прямой отношения «больше» и «меньше» для обыкновенных дробей. Сравнивать дроби с равными знаменателями. Применятьразличные приёмы сравнения дробей с разными знаменателями, выбирая наиболее подходящий приём в зависимости от конкретной ситуации. Находить способы решения задач, связанных с упорядочиванием и сравнением дробей
8.6. Натуральные числа и дроби		117—119 (ч. 1)	П-25, «Проверь себя»	Моделироватьв графической и предметной форме существование частного для любых двух натуральных чисел. Оперироватьсимвольными формами: записыватьрезультат деления натуральных чисел в виде дроби, представлять натуральные числа обыкновенными дробями. Решать текстовые задачи, связанные с делением натуральных чисел, в том числе задачи из реальной практики
Обзор и контроль		Моделировать в графической, предметной форме понятия и свойства, связанные с понятием обыкновенной дроби. Записывать и читать обыкновенные дроби. Соотноситьдроби и точки на координатной прямой. Преобразовывать дроби, сравнивать и упорядочивать их. Проводитьнесложныеисследования, связанные со свойствами дробных чисел, опираясь на числовые эксперименты

Основные цели: сформировать понятие дроби, познакомить учащихся с основным свойством дроби и научить применять его для преобразования дробей, научить сравнивать дроби, сформулировать на интуитивном уровне начальные вероятностные представления.

Обзор главы. В предлагаемом курсе обыкновенные дроби целиком изучаются до десятичных. И в дальнейшем изложение десятичных дробей строится на естественной математической базе с опорой на знания об обыкновенных дробях.

Основной акцент в данной главе делается на создание содержательных представлений о дробях. Одновременно здесь закладываются умения решать основные задачи на дроби, сокращать дроби и приводить их к новому знаменателю, сравнивать дроби.

Изучение каждого пункта целесообразно предварять выполнением соответствующей серии практических заданий из рабочей тетради (закрашиванием долей фигуры, сравнением дробей с использованием рисунков, обращением долей в более мелкие и в более крупные и т. д.), способствующих формированию наглядно-образных представлений о формируемых понятиях.

Материалы для контроля.

Пособие «Контрольные работы». Зачёт 5. Обыкновенные дроби.

Пособие «Тематические тесты». Тест 6. Доли и дроби. Тест 7. Основное свойство дроби. Преобразование дробей.

Доли

Методический комментарий

Основное назначение этого пункта — создание содержательной основы для введения понятия дроби. Дробь — это математический способ выражения долей. С понятием доли учащиеся знакомы с начальной школы; оно тесно связано с их жизненным опытом. И на этих уроках необходимо прежде всего убедиться, что учащиеся знают названия долей (понимают и умеют правильно употреблять в речи). Они должны понимать, что для нахождения половины (трети, четверти и т. д.) некоторой величины её нужно разделить на две (три, четыре и т. д.) равные части; чем больше частей, на которые мы делим, тем меньше получается доля. Желательно, чтобы учащиеся получили возможность реально на практике выделять доли целого, поэтому на уроках полезно иметь «подсобный материал» — проволоку, шнур, разрезные модели, плакаты с изображением геометрических фигур, изготовленные из бумаги прямоугольники, квадраты, круги и т. д.

В упражнениях к пункту закладываются основы для восприятия некоторых важных идей, которые получают развитие в дальнейшем, — это основное свойство дроби (упражнение 605), нахождение части от целого и целого по его части (упражнения 606—608,610 и др.). При выполнении заданий учащиеся должны проговаривать решение вслух.

Комментарий к упражнениям

611, 612. Полезные задания, позволяющие повторить соотношения между единицами длины и между единицами массы. Кроме того, оно обучает способу рассуждений в тех случаях, когда требуется выяснить, какую часть одна величина составляет от другой. Для наглядности при выполнении упражнения 611 можно использовать шкалу линейки. Задания желательно выполнить в классе.

615. Условие каждой задачи желательно разобрать с помощью схематического рисунка. Вообще, всегда, когда для наглядности можно воспользоваться рисунком, надо это делать.

Что такое дробь

Методический комментарий

В содержании пункта выделено несколько фрагментов. Первые два из
них — понятийные. Они включают в себя само понятие «дробь», раскрытие его содержательного смысла, а также понятия «правильная дробь» и «неправильная дробь». Усвоение этого материала обеспечивается упражнениями 620—631 из группы А и поддерживается упражнениями 643, 644 из группы Б. Принципиально важными здесь являются задания, предусматривающие работу с рисунком (упражнения 620—622), и соответствующие задания из рабочей тетради. В ходе их выполнения формируются образы, составляющие чувственную основу таких умений, как нахождение указанной части целого и выражение дробью заданной части величины. Выполняя эти задания, ученики должны давать вслух развёрнутые пояснения (см. комментарий к упражнению 620). И только после этого можно перейти к упражнениям 623—627 из учебника, требующим фактически тех же рассуждений.

Следующий фрагмент — изображение дробей точками координатной прямой. Этот материал сложен для учащихся, и всё же надо стремиться к тому, чтобы каждый ученик овладел соответствующим приёмом. Заметим, что приём изображения дроби точкой на координатной прямой не сформулирован в учебнике в виде общего правила, а разъяснён на примере конкретной дроби. Этот пример можно рассматривать как образец рассуждения ученика. Способ построения точки с данной координатой вытекает из самого смысла понятия дроби: знаменатель показывает, на сколько равных частей нужно разделить единичный отрезок, а числитель — сколько таких частей надо взять. При этом ученики должны научиться выбирать отрезок, удобный для построения указанных дробей. Усвоению этого материала будут способствовать упражнения 632—634 из группы А, а также 645, 646 из группы Б, причём их целесообразно предварить выполнением заданий на готовом чертеже, которые помещены в рабочей тетради.

И наконец, последний фрагмент — решение задач на дроби (нахождение части от целого и целого по его части). Этот материал представлен в системе упражнений учебника (упражнения 635—642 и 647—650) и в дидактических материалах. Это первый этап в решении таких задач и никаких правил здесь формулировать не следует. Основу решения составляет понимание смысла дроби. Необходимо обратить внимание учащихся на то, что ключом к решению рассматриваемых задач является отыскание одной доли. Это должно проявиться в пояснениях к выполняемым действиям. Осознанию учащимися способа рассуждений будет способствовать изображение условия задачи в виде схематического рисунка. Заметим, что последние задачи в учебнике и дидактических материалах достаточно сложные (см., например, упражнение 650 из учебника), и целесообразность обращения к ним на этом этапе определяется только с учётом возможностей детей.

Комментарий к упражнениям

620. Проведём рассуждения для рисунка ж: квадрат разделён на 6 равных частей, поэтому каждая часть составляет 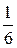квадрата; 2 части закрашены, значит, закрашено 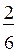квадрата; 4 части не закрашены, т. е. не закрашено 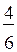квадрата.

Такие же рассуждения следует проводить при выполнении аналогичных заданий из рабочей тетради.

625. а) Рассуждения могут быть такими: всего мячей 8; один мяч составляет 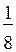всех мячей; синих мячей 3, они составляют 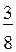всех мячей; красных мячей 5, они составляют 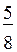всех мячей.

633, 634. Полезно обсудить, почему выбраны именно такие единичные отрезки и какие другие удобно было бы взять (число клеток должно делиться на знаменатели изображаемых дробей).

638. Результат получается больше исходного числа, так как в условии дана неправильная дробь.

650. а) Когда взяли половину всех книг, то ещё осталось 1 + 2 книги, т. е., иначе говоря, оставшиеся 3 книги — это половина всех книг. Поэтому всего на столе лежало 6 книг. Решение полезно проиллюстрировать, взяв 6 книг и выполнив описанные в задаче действия.

Основное свойство дроби

Методический комментарий

Как и в предыдущих пунктах, формулировке основного свойства следует предпослать работу с геометрическими моделями (см. рабочую тетрадь), в ходе которой учащиеся осознают возможность выражения одной и той же части целого разными дробями и без каких-либо формальных приёмов поупражняются в замене одной дроби другой, ей равной. После этого можно перейти к изложению материала по учебнику.

Обращаем внимание учителя на необходимость тщательно следить за речью учащихся и их записями в процессе применения основного свойства дроби. (Вот типичный неверный оборот речи: «Умножим дробь на одно и то же число».)

В пункте рассматривается два вида преобразования дробей с помощью основного свойства: приведение дроби к новому знаменателю и сокращение дроби. Здесь соответствующие умения только начинают формироваться; их развитие будет происходить на протяжении изучения всей темы «Дроби» в 5 классе, а также в 6 классе.

Здесь и далее в качестве устных упражнений можно предлагать вопросы и задания типа:

1) Приведите дробь 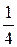к знаменателям 8, 12, 20, 36. Замените эту дробь ещё какой-нибудь равной дробью со знаменателем, отличным от указанных. Можно ли привести эту дробь к знаменателю 22?

2) Можно ли привести дробь 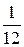к знаменателю 24? к знаменателю 30? Почему? Дайте пояснение, используя термин «кратный».

3) Назовите несколько знаменателей, к которым можно привести дроби

При выполнении заданий на сокращение дробей учащиеся не обязаны сразу же делить числитель и знаменатель на наибольший общий множитель, а имеют право сокращать дробь последовательно. Задания на сокращение дробей предоставляют естественную возможность повторить признаки делимости.

Комментарий к упражнениям

656—663. Целью этих упражнений, помимо выработки технических навыков, является осознание того, что дробь можно привести к любому знаменателю, кратному исходному. Желательно, чтобы учащиеся в результате выполнения подобных заданий научились перечислять знаменатели (в пределах первых тридцати, пятидесяти, первых ста чисел), к которым может быть приведена данная дробь (например, дроби

663. Перебирая знаменатели дробей, устанавливаем, что 36 делится на 12, 9, 6, 4, 3, 2. Поэтому к знаменателю, равному 36, можно привести такие дроби: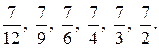

674—678. Это серия упражнений на тему «Какую часть…?». Такие упражнения детям уже встречались при изучении предыдущих пунктов. Новым является то, что дробь, выражающую указанную часть величины, теперь ещё приходится сокращать.

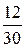677. а) Ученики могут дать такое развёрнутое объяснение: одна девочка составляет часть класса, тогда 12 девочек составят класса, т. е. 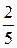класса.

Заметим, что сильные учащиеся уже, возможно, сумеют сразу же записать результат в виде дроби 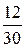. Это следует приветствовать, но тем не менее полезно предложить кому-нибудь из класса дать пояснение.

б) Подробное решение можно записать так:

20 + 12 = 32 — столько деревьев растёт в саду;

— такую часть всех деревьев составляет одно дерево;

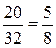— такую часть всех деревьев составляет 20 яблонь;

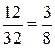— такую часть всех деревьев составляет 12 слив.

Если учащиеся овладели свёрнутым алгоритмом рассуждений, то вторую строчку в записи решения можно опустить.