Как обозначают и сравнивают углы
Методический комментарий
Угол для учащихся новая и весьма специфическая фигура, измерение углов осваивается ими со значительно большими трудностями, чем измерение длин. Это связано с тем, что в их практическом, жизненном опыте интуитивные представления об угле как о геометрической фигуре и об измерении углов практически отсутствуют. Для того чтобы школьники «освоились» с этой фигурой, требуется определённое время. Поэтому упражнения, аналогичные тем, которые даются в данной главе, следует «вкрапливать» в последующие уроки.
Важным результатом изучения данного пункта является умение сравнить два угла (на глаз, наложением, используя кальку или углы, вырезанные из бумаги). При этом может выясниться, что ученик не овладел самим понятием угла. Это становится очевидным в том случае, если ученик утверждает, что угол А больше угла В, так как у него «стороны длиннее». Очевидно, что, не преодолев эту трудность, нет смысла переходить к измерению углов. Помочь в этом случае может использование различных моделей.
Умение увидеть прямой угол в различных положениях и конфигурациях, построить, используя угольник или клетчатую бумагу, является весьма важным, так как это в определённом смысле опорное понятие (острый угол и тупой угол вводятся как углы соответственно меньший и больший прямого). Следует обращать внимание на то, чтобы учащиеся строили углы в различных положениях.
Используя клетчатую бумагу, легко построить прямой угол, когда вершина угла лежит в узле сетки, а стороны угла идут по линиям сетки. Если позволяет время, можно показать более сильным учащимся, как построить угол и в ином положении. Пусть точка О — вершина угла, а сторона угла проходит через точку сетки, расположенную от вершины на две клетки вправо и одну вверх. С помощью угольника проведём другую сторону угла. Учащиеся должны увидеть, что она проходит через точку, расположенную от вершины на одну клетку влево и две вверх (рис. 18).
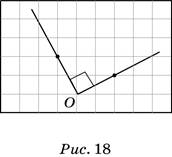
Проведём сторону второго угла через точку сетки, расположенную от вершины на одну клетку вправо и три клетки вверх. Другая сторона прямого угла пройдёт через точку, расположенную от вершины на три клетки влево и одну клетку вверх. Подметив закономерность, учащиеся могут сами отметить пару точек, ей удовлетворяющих (например, четыре вправо и пять вверх — пять влево и четыре вверх), и проверить с помощью угольника, является ли построенный по этим точкам угол прямым.
Комментарий к упражнениям
372. Учащиеся должны перенести угол А на кальку и наложить его на другие углы.
373.Чертёж можно сделать на кальке и сравнить углы, перегнув лист по прямой ОВ.
380.Сравнить углы АОС и BOD можно так. Пары углов AOD и DOB, АОС и СОВ составляют развёрнутый угол. Так как угол AOD больше угла СОВ, то угол, дополняющий угол AOD до развёрнутого, должен быть меньше, чем угол, дополняющий угол СОВ до развёрнутого. Значит, угол DOB меньше угла АОС.
381. 2) На основании решения первой задачи этого упражнения часть учащихся может догадаться, что, для того чтобы угол ABC был прямым, нужно провести диаметр АС. Другие же увидят, что АС — диаметр окружности, после построения прямого угла с помощью угольника.
Измерение углов
Методический комментарий
Ещё одна трудность, возникающая при измерении углов, связана со знакомством с новым измерительным инструментом — транспортиром.
В течение трёх лет обучения в начальной школе учащимся была известна только одна шкала — шкала линейки. Поэтому, чтобы избежать связанных с этим ошибок, полезно провести сравнение шкалы транспортира со шкалой линейки, обращая внимание на их сходство и различия: цена меньшего деления на линейке — 1 мм, на транспортире — 1°, большее деление на линейке — 10 мм (1 см), на транспортире — 10°.
В качестве самых первых упражнений на измерение и построение углов должны быть использованы задания из рабочей тетради, где часть действий уже выполнена — «транспортир» приложен необходимым образом. Для некоторых учащихся число таких упражнений может быть увеличено; можно предложить учащимся скопировать транспортир на лист бумаги, а полученное изображение использовать при дальнейшей работе.
Обращаем внимание учителя на то, что задания на построение углов даны в рабочей тетради, так как строить углы целесообразнее на нелинованной бумаге. Клетчатую бумагу можно использовать там, где необходимо строить углы в 90°, 45°, 135°. Уметь строить прямой угол на гладкой бумаге учащиеся должны с помощью как транспортира, так и угольника.
Продолжается работа, направленная на развитие глазомера: учащимся предлагаются упражнения, где требуется приближённо оценить величину угла. С этой же целью полезно добавить упражнения типа: «Постройте без помощи транспортира углы, равные 30°, 40°, 80°, 100°». Задание может выполняться как на нелинованной, так и на клетчатой бумаге.
Для того чтобы учащиеся могли по клеткам приближённо строить углы в 10° 20°, ..., 80°, можно провести следующую практическую работу.
1) Построить с помощью транспортира углы, равные 10°, 20°, ..., 90° с вершиной в узле сетки (рис. 19) и общей стороной, идущей по горизонтальной линии сетки.
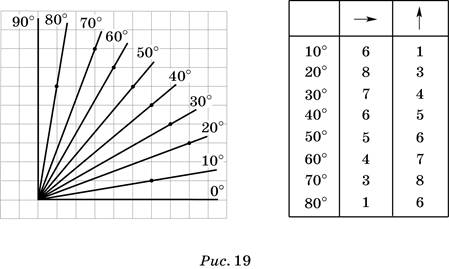
2) Отметить ближайший узел сетки, через который прошла другая сторона каждого угла.
3) Определить «путь» из вершины угла в отмеченную точку и занести его в таблицу.
4) Сравнить данные таблицы для углов 10° и 80°, 20° и 70° и т. д.
5) По данным таблицы построить угол, приближённо равный, например, 30°.
В качестве дополнительных упражнений можно предложить учащимся задачи на уравнивание с геометрической фабулой. Например, можно дать такую задачу: «Сумма двух углов равна 120°, а один угол больше другого на 20°. Чему равен каждый угол? Начертите эти углы».
Комментарий к упражнениям
399. 1) Начать можно с практических построений. По ходу построений учащиеся догадаются, что три угла по 60° составят один развёрнутый угол и ещё три угла — другой развёрнутый угол, т. е. полный круг равен 360°.
2) Четыре луча, проведённые из одной точки под углом 90°, делят плоскость на четыре прямых угла. Следовательно, чтобы все углы были острыми, достаточно провести пять лучей (рис. 20).
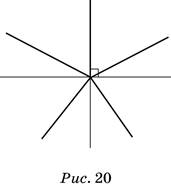
В рабочей тетради есть задание, в котором требуется разделить окружность на 6 равных дуг. Начать его выполнение можно так. Проведя диаметр окружности, разделим её на две равные части, после чего уже с помощью транспортира каждую полуокружность разделим на три равные части. Здесь можно обратить внимание учащихся на тот факт, что круг
равен 360°.
Если выполнение этого упражнения отложить до изучения следующего пункта, то можно расширить задание и попросить учащихся последовательно соединить точки деления отрезками. Таким образом они построят шестиугольник, все стороны и все углы которого равны. (Термин «правильные многоугольники» вводится в 6 классе.) Аналогичным образом, разделив окружность на три, на четыре части, они могут построить равносторонний треугольник, квадрат.
Ломаные и многоугольники
Методический комментарий
Расширение представлений учащихся о многоугольниках происходит через знакомство с элементами многоугольников и с понятиями диагонали и периметра многоугольника. Учащиеся учатся воспринимать геометрическую фигуру не как единое целое, а как объект, состоящий из определённых элементов, учатся видеть фигуры, образующиеся при eё разбиении (см., например, упражнение412).
Важно научить их приёмам, позволяющим облегчить задачу восприятия, особенно в случаях сложных конфигураций. Это и использование графических приёмов: раскрашивание одной или нескольких фигур, входящих в данную конфигурацию, обведение контуров отдельных фигур, использование при этом цвета. Это и поиск равных фигур и элементов, поиск симметрии. Это и определённая логика перебора, позволяющая вычленить, увидеть все требуемые фигуры и одновременно доказать отсутствие других фигур.
Определённое внимание уделяется понятию периметра многоугольника. Заметим, что этот термин может оказаться для учащихся новым. Периметр многоугольника здесь определяется как длина границы. При таком подходе облегчается создание опорного зрительного образа, соответствующего данному понятию. Этому будет способствовать разъяснение происхождения термина «периметр» («измеряю вокруг»), а также практические измерения (длины границы фигуры, вычерченной на бумаге; длины ограды земельного участка), сгибание из проволоки различных фигур с одинаковым периметром и др.
Здесь необходимо также продолжать формирование умения измерять углы и строить углы заданной величины.
Комментарий к упражнениям
415. Задача трудная, однако её целесообразно рассмотреть и в слабом классе, упростив условие.
Сначала следует внимательно рассмотреть рисунок: увидеть большой пятиугольник, «звезду», маленький пятиугольник, различные треугольники. Можно предложить учащимся найти какой-нибудь треугольник, равный треугольнику АОВ (такой же, как треугольник АОВ), треугольнику ABC и др., назвать хотя бы один треугольник со стороной АВ, несколько треугольников с вершиной В. Чтобы облегчить выполнение этого задания, можно, скопировав рисунок на лист бумаги, раскрасить карандашами двух цветов маленькие треугольники разных видов. Учащимся значительно проще будет увидеть треугольник, составленный, например, из красного и синего треугольников, из двух красных и одного синего треугольника и т. д.
Чтобы найти все 35 треугольников, предлагается следующая логика перебора. Пятиугольник разбит на треугольники двух видов и пятиугольник. Будем составлять треугольники из различных комбинаций этих трёх фигур. Чтобы при подсчёте не потерять ни один из треугольников, важно выбрать направление обхода, например по часовой стрелке. Началом обхода будем считать вершину В.
Подсчитаем число маленьких треугольников, равных, например, треугольнику АВО и треугольнику OBF. Тех и других будет по 5. Далее рассмотрим треугольник ABF, составленный из треугольников АВО и OBF, и подсчитаем такие треугольники. Их всего 10 (по два у каждой вершины). Треугольник ABC составлен из трёх треугольников — АВО, OBF и FBC. Таких треугольников тоже 5. Понятно, что никакие четыре, пять и т. д. маленьких треугольников новые треугольники не образуют.
Теперь рассмотрим маленький пятиугольник. Присоединение к нему одного из маленьких треугольников треугольника не даёт. Присоединив же к нему, например, треугольники АОK и FCG, получим треугольник АСН. Число треугольников такого вида равно числу вершин маленького пятиугольника — 5. И наконец, подсчитаем число треугольников типа BDE, составленных из пятиугольника и четырёх треугольников. Снова обойдём все вершины пятиугольника, начиная с вершины B, и получим ещё 5 треугольников. Итого 35 треугольников.
По ходу решения можно заполнить таблицу:
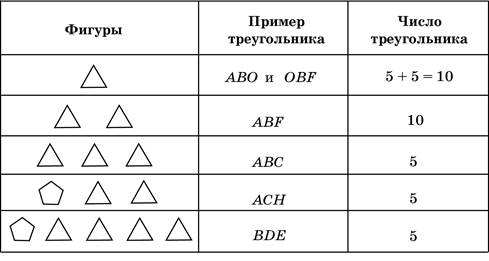
Несколько комментариев к заданиям из рабочей тетради.
В рабочей тетради есть задание, в котором требуется измерить величины углов треугольников. Не следует торопить события и сообщать учащимся, что сумма углов треугольника равна 180° — упражнение такой цели не преследует. Этому факту будет посвящён отдельный пункт в 6 классе. Здесь же отрабатываются простейшие умения: видеть углы треугольника, уметь их измерять, записывать величину угла.
Обращаем внимание на то, что если в задании требуется найти середину отрезка, то учащиеся находят её с помощью линейки.
Чтобы определить, от какого из треугольников «оторван» угол, нужно дорисовать «оторванные» треугольники и измерить их величины.
Вполне возможно, что у некоторых учащихся уже сложился образ выпуклого четырёхугольника с проведённой в нём диагональю, которая и делит его на два треугольника. Но, скорее всего, таких учащихся окажется немного, поэтому искать решение задач о разбиении четырёхугольника нужно практически. Пусть сначала учащиеся проведут прямую, проходящую через две противоположные стороны четырёхугольника. Они получат два четырёхугольника. Затем эту прямую можно «развернуть» и провести через сторону и вершину треугольника. В этом случае получатся треугольник и четырёхугольник. Если прямую провести через две соседние стороны четырёхугольника, то получатся треугольник и пятиугольник, что явно дальше от нужного решения. Таким образом, становится очевидным, что прямая должна проходить через две вершины четырёхугольника.
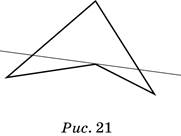
Решение задачи о разбиении невыпуклого четырёхугольника изображено на рисунке 21.
Глава 6. Делимость чисел (15 уроков)
Примерное поурочное планирование учебного материала
| Пункт учебника | Число уроков | Дидактические материалы | Характеристика деятельности учащихся | |
| 6.1. Делители и кратные | О-22, П-18 | Формулировать определения понятий «делитель» и «кратное» числа, употреблять их в речи. Находить делители и кратные данных чисел, наибольший общий делитель и наименьшее общее кратное двух чисел, использовать соответствующие обозначения. Анализировать ряды кратных. Решать текстовые задачи, связанные с делимостью чисел | ||
| 6.2. Простые и составные числа | О-23 | Формулировать определения простого и составного числа, иллюстрировать их примерами. Выполнять разложение числа на простые множители. Использоватьматематическую терминологию для объяснения, верно или неверно утверждение. Находить простые числа с помощью «решета Эратосфена». Выяснять, является ли число составным. Использоватьв ходе решения задач таблицу простых чисел | ||
| 6.3. Свойства делимости | — | Формулировать свойства делимости суммы и произведения, рассуждать, обращаясь к соответствующим формулировкам. Конструировать математические утверждения с помощью связки «если…, то…». Использоватьтермин «контрпример», опровергать утверждение общего характера с помощью контрпримера | ||
| 6.4. Признак делимости | О-24, П-19 | Формулировать признаки делимости на 2, на 5, на 10, на 3, на 9. Приводить примеры чисел, делящихся и не делящихся на какое-либо из указанных чисел, давать развёрнутые пояснения. Конструировать математические утверждения с помощью связки «если…, то…». Применять признаки делимости в рассуждениях. Доказывать и опровергать утверждения | ||
| 6.5. Деление с остатком | — | Выполнять деление с остатком при решении текстовых задач и интерпретировать ответ в соответствии с поставленным вопросом. Классифицироватьнатуральные числа по остаткам от деления | ||
| Обзор и контроль | Применятьпонятия, связанные с делимостью натуральных чисел. Использовать свойства и признаки делимости.Опровергать с помощью контрпримеров утверждения о делимости чисел. Решать задачи на деление с остатком |
Основные цели:сформировать у учащихся базовые знания, относящиеся к вопросу делимости натуральных чисел (понятие делителя и кратного, простого и составного числа, разложение на простые множители, деление с остатком), познакомить со свойствами и признаками делимости.
Обзор главы. Эта глава — завершающий этап в изучении натуральных чисел. Здесь рассматриваются элементарные понятия теории делимости. От предыдущих глав этот материал отличается тем, что он содержит значительный объём теоретических сведений, их освоение представляет для учащихся определённые трудности. В то же время у учащихся появляется хорошая возможность приобрести опыт проведения несложных доказательных рассуждений. Нельзя также упускать из виду то обстоятельство, что учение о целых числах — неисчерпаемое поле для математических исследований, которые веками привлекали больших учёных. Здесь естественным образом возникают задачи, которые по своему содержанию, по постановке вопроса понятны даже младшим школьникам. Некоторые из них, естественно, в адаптированном виде представлены в практической части данной главы.
Материалы для контроля.
Пособие «Контрольные работы». Зачёт 4. Делимость чисел.
Пособие «Тематические тесты». Тест 5. Делимость чисел.
Делители и кратные
Методический комментарий
Пункт начинается с определения операции деления. Это определение известно учащимся с начальной школы, они возвращались к нему и в курсе
5 класса. Теперь это определение выступает как основа, стержень теоретической части главы «Делимость чисел». Оно даётся в формулировке, разъясняющей смысл оборота речи «число а делится на число b».
На базе этого определения вводятся два взаимосвязанных понятия — «делитель» и «кратное». Учащиеся должны научиться трактовать числовые равенства вида a = b · c, где a, b, c — натуральные числа, с использованием указанных терминов. Например, из равенства 30 = 5 · 6 следует, что число 5 — делитель 30, а число 30 — кратное 5 (такие же утверждения можно сформулировать по отношению к паре чисел 6 и 30). Учащиеся должны также уметь проверять, является ли одно из двух чисел делителем (кратным) другого. На отработку этих умений направлены упражнения 419—421, а в начале объяснительного текста содержатся образцы соответствующих рассуждений (число 18 делится на 3, так как 18 = 3 · 6; число 18 не делится на 4, так как 4 · 4 < 18, а 4 · 5 > 18).
Далее в ходе рассмотрения примеров вводится ещё ряд новых терминов: общий делитель, наибольший общий делитель, общее кратное, наименьшее общее кратное. Они появляются естественным образом, как слова русского языка, без каких-либо специальных определений. Поэтому учащимся не могут предлагаться вопросы типа: «Что называется наибольшим общим делителем чисел а и b?» В то же время обозначения НОД и НОК учащиеся должны знать, понимать и уметь использовать в своих записях.
Остановимся на вопросе нахождения НОД и НОК. Прежде всего отметим, что в курсе не предусмотрено рассмотрение известных алгоритмов нахождения НОД и НОК с помощью разложения чисел на простые множители. Во-первых, эти алгоритмы сложны и недоступны для пятиклассников, во-вторых, техническая составляющая современного общеобразовательного курса математики не требует столь продвинутых навыков. Поэтому для нахождения наименьшего общего кратного двух чисел предлагается следующий простой алгоритм, основанный на формируемых в данном пункте базовых знаниях и умениях: выписывается ряд чисел, кратных большему числу; первое число в этом ряду, которое делится и на второе из данных чисел, будет их наименьшим общим кратным. Так как в заданиях предлагаются, как правило, небольшие числа (см. упражнения 434, 435), то перебор заканчивается быстро. Умение находить наименьшее общее кратное совершенствуется в ходе изучения темы «Дроби» при приведении дробей к наименьшему общему знаменателю. Там уже рассматриваются и фиксируются в сознании учащихся разные случаи (одно из чисел кратно другому и т. д.).
Что касается нахождения НОД пары чисел, то соответствующее умение не входит в перечень обязательных требований. В связи с этим упражнения 425 и 426 направлены не столько на выработку такого умения, сколько на осознание самого понятия. В то же время умение найти с помощью перебора все делители данного числа является существенным. Подобного рода задания предлагаются, как правило, для небольших чисел; их выполнение базируется на знании таблицы умножения (см. упражнения 422 и 423).
В систему упражнений пункта включены несколько сюжетных задач (см. упражнения 427, 428, 436, 437, 440—442), математическая сущность которых состоит в нахождении общих делителей или общих кратных, указанных в условии чисел. Важно, чтобы учащиеся осознали связь содержания задачи с изучаемыми понятиями, увидели возможность их применения в практических ситуациях.
Комментарий к упражнениям
422.Удобно выписать делители парами, а потом уже их упорядочить.
423.Нужно найти все делители и потом ответить на вопрос задачи.
424. а) Решение сводится к нахождению всех делителей числа 36, отличных от 1 и самого этого числа. Так как делителями числа 36 являются числа 2, 3, 4, 6, 9, 12, 18, то количество одинаковых порций, на которые можно разделить 36 конфет, равно 2, 3, …, 18. Всего 7 способов.
Дополнительный вопрос: сколько конфет будет в одной порции при каждом способе деления? (Если умозрительно детям рассуждать трудно, то можно раскладывать реальные конфеты.)
б) Сначала нужно найти все возможные способы деления 24 учеников на одинаковые группы (см. задачу «а»)).
427.18 синих палочек можно разложить на 2, 3, 6 и 9 одинаковых кучек; 12 жёлтых палочек можно разделить на 2, 3, 4 и 6 одинаковых кучек. Чтобы разложить все палочки в одинаковые кучки, в которых будут и синие, и жёлтые палочки, есть всего три способа: 2 кучки (по 9 синих и 6 жёлтых палочек), 3 кучки (по 6 синих и 4 жёлтых палочки), 6 кучек (по 3 синих и
2 жёлтых палочки). Задача свелась к нахождению общих делителей чисел
18 и 12. (Обязательно надо либо разложить реальные палочки, либо сделать рисунок.)
429—432. Перед выполнением этих заданий надо внимательно разобрать в учебнике фрагмент, связанный с построением и обсуждением особенностей ряда чисел, кратных 10 (см. с. 114).
431. Надо двигаться от числа 70 влево и вправо, отнимая и прибавляя 14. Получим такой ряд кратных: 14, 28, 42, 56, 70, 84, 98, 112, 126, 140.
432. Задача, обратная по отношению к упражнению 430. Так как
60 : 12 = 5, то это ряд кратных числа 5. Далее: 5 · 1 = 5, 5 · 6 = 30, 5 · 20 = 100.
436.При счёте тройками называют числа 3, 6, 9, 12, 15, 18, 21, 24, 27, 30, 33, ... . При счёте пятёрками называют числа 5, 10, 15, 20, 25, 30, 35, 40, 45, ... . Числа 15, 30, ... называют и когда считают тройками, и когда считают пятёрками. Но Маша задумала число, меньшее 30, т. е. число 15.
437. Общее число яиц должно делиться и на 10, и на 12. Можно выписать все такие числа, большие 100 и меньшие 150.
На 10 делятся числа 110, 120, 130, 140. На 12 делятся числа 108, 120, 132, 144. Значит, это число 120.
440. Первый автобус приходит на конечную остановку через 30 мин,
60 мин, 90 мин, 120 мин, 150 мин и т. д. Второй автобус приходит на конечную остановку через 40 мин, 80 мин, 120 мин, 160 мин и т. д. Первое совпадение времени — через 120 мин.
После того как задача будет решена перебором, следует обратить внимание учащихся на то, что фактически нам пришлось искать наименьшее число, которое делится и на 30, и на 40, т. е. HOK (30, 40).
441. Задача также может быть решена перебором. Однако в техническом отношении он сложнее, чем в предыдущей задаче. Поэтому проведём такое рассуждение.
Расстояние, на котором будет замечено первое совпадение следов, — это наименьшее число, которое делится и на 50, и на 60, т. е. это 300 см. Это расстояние укладывается в 141 м 47 раз.
442. Три автобуса окажутся на остановке через 30 мин, т. е. в 9 ч 15 мин. Два автобуса окажутся на остановке одновременно первый раз через 6 мин, т. е. в 8 ч 51 мин.
Простые и составные числа
Методический комментарий
В результате изучения пункта учащиеся должны знать определения простого и составного числа и владеть кругом элементарных представлений о простых числах (наименьшее простое число — это 2, простых чисел бесконечно много, существуют специальные таблицы простых чисел); знать простые числа в пределах нескольких первых десятков; распознавать двузначные и трёхзначные простые числа, прибегая при необходимости к помощи таблицы; раскладывать составное число на простые множители (формирование последнего умения будет продолжено при изучении признаков делимости, где учащиеся познакомятся с удобным приёмом разложения числа на простые множители).
В содержании пункта предусмотрен небольшой исторический экскурс — знакомство с «решетом Эратосфена». Желательно, чтобы это знакомство прошло в активной форме, т. е. чтобы ученики выполнили по шагам процедуру, описанную в учебнике. Можно также дополнительно сообщить, что по мере продвижения в область больших чисел простые числа встречаются всё реже, но наибольшего простого числа нет. Если будет рассматриваться упражнение 454, в котором речь идёт о числах-близнецах, то можно добавить, что известны весьма большие «близнецы» (например, 10 006 427 и 10 006 429). Существует гипотеза, согласно которой среди простых чисел имеется бесконечно много пар «близнецов».
Комментарий к упражнениям
449. Надо показать, что число можно разложить на множители, каждый из которых отличен от 1.
450. 3) Нет, не всегда. Простых чисел нет в последовательности чисел, оканчивающихся цифрой 2, 4, 5, 6, 8. Если простые числа есть, то их несколько.
452—454. Выполняются путём рассмотрения и анализа таблицы простых чисел.
456. При записи разложений нужно использовать степени. Решение может выглядеть так: 4 = 2 · 2 = 22; 6 = 2 · 3; 8 = 2 · 2 ·2 = 23; 9 = 3 · 3 = 32 и т. д.
457. Запись решения пятиклассниками, которые ещё не знают свойства степени, может выглядеть так: 10 = 2 · 5; 100 = 10 · 10 = 2 · 5 · 2 · 5 = 22 · 52 и т. д.
459. с = 1 · 2 · 3 · 4 · 5 · 6 · 7 · 8 · 9 · 10 = 1 · 2 · 3 · 2 · 2 · 5 · 2 · 3 · 7 · 2 · 2 ×
× 2 · · 3 · 3 · 2 · 5. Теперь посчитаем, сколько в разложении двоек, сколько троек, сколько пятёрок и запишем результат с помощью степеней. Получим
с = 28 · 34 · 52 · 7.
461. 2) Каждое из чисел 6, 10 и 21 есть произведение двух простых чисел. Таким же свойством обладают, например, числа 2 · 11 = 22, 3 · 5 = 15,
7 · 5 = 35. Каждое такое число имеет 4 делителя. Например, делителями числа 15 являются 1, 3, 5 и 15.
3) 4 делителя: 1, а, b и а · b.
Свойства делимости
Методический комментарий
В пункте рассматриваются свойства делимости произведения и суммы. Их обоснование проводится путём рассмотрения доказательных примеров, которые, однако, носят общий характер. Идея доказательства знакома учащимся: чтобы показать, что значение рассматриваемого числового выражения (произведение или суммы) делится на некоторое число а, это выражение нужно представить в виде произведения, в котором один из множителей равен а. Поэтому приведённые в учебнике рассуждения должны быть доступны детям. Тем не менее рекомендуем их разбирать в ходе фронтальной работы учителя с классом, не требуя в дальнейшем от учащихся их воспроизведения.
Упражнения к пункту подобраны таким образом, что учащимся для обоснования всегда достаточно сослаться на соответствующее свойство. Формулировки свойств должны быть многократно проговорены вслух (или прочитаны по учебнику), это будет способствовать их постепенному запоминанию.
В пункте сделан определённый шаг на пути повышения логической культуры учащихся. Речь идёт о введении термина «контрпример», о разъяснении способа опровержения общего утверждения с помощью контрпримера. Заметим, что учащимся не раз приходилось иметь дело с опровергающими примерами, но теперь, как говорится, вещи названы своими именами.
Комментарий к упражнениям
468. а) Найдём простые делители каждого из множителей. Число 6 делится на 2 и на 3, число 15 делится на 3 и на 5, число 77 — на 7 и на 11. Значит, простые делители произведения 6 · 15 · 77 — это числа 2, 3, 5, 7, 11.
469. б) Делителем числа n является также и любой делитель числа 18, т. е. это числа 2, 3, 6, 9.
471. В сильном классе можно не ограничиваться указаниям трёх подходящих чисел, а выйти на обобщение.
а) Можно подставить любое число, кратное 5.
б) Можно подставить любое число, кратное 8.
в) Так как произведение 6 · n содержит множитель 2, то можно подставить любое число, кратное 5.
г) Любое число, кратное 5.
472. Верное надо обосновать, сославшись на соответствующее свойство, а неверное опровергнуть с помощью контрпримера.
476. Имеем 5 · 29 + 5 · 17 = 5 · (29 + 17) = 5 · 46 = 5 · 2 · 23. Простыми делителями, кроме числа 5, являются числа 2 и 23. Составные делители — это числа 10, 46, 115, 230.
477. 2) а) Сумма двух чётных чисел — число чётное. Докажем это, проведя рассуждения.
Чётное число делится на 2. По свойству делимости сумма двух чисел, делящихся на 2, тоже делится на 2. Значит, эта сумма есть число чётное.
б) Сумма чётного числа и нечётного есть число нечётное. В самом деле, чётное число — это число, делящееся на 2; нечётное число — это число, не делящееся на 2. Если одно слагаемое делится на 2, а другое не делится, то сумма на 2 не делится. Значит, сумма — число нечётное.
478. 2) Разбиение на слагаемые может быть разным. Например:
а) 128 = 80 + 48;
б) 238 = 220 + 18;
в) 385 = 330 + 55.
479. а) Сумма двух простых чисел может быть и простым числом, и составным. Примеры: 3 + 2 = 5, 5 + 2 = 7, 11 + 2 = 13, 17 + 2 = 19 — эти суммы являются простыми числами; 3 + 5 = 8, 7 + 2 = 9, 5 + 13 = 18 — эти суммы являются составными числами. Учащиеся могут выйти на интересное обобщение: чтобы сумма двух простых чисел оказалась простым числом, одним из слагаемых обязательно должно быть число 2. В самом деле, если сложить два нечётных простых числа, то сумма будет числом чётным, а значит, составным.
б) Произведение двух простых чисел всегда есть число составное.
Признаки делимости
Методический комментарий
В пункте рассматриваются две группы признаков. Это признаки делимости на 2, на 5 и на 10 (в них делимость устанавливается по последней цифре числа) и признаки делимости на 3 и на 9 (в них вопрос о делимости решается по сумме цифр числа). Кроме того, при работе по дидактическим материалам учащиеся могут познакомиться с признаками делимости на 4 и на 25 (в этих признаках делимость также устанавливается по последней цифре числа: так, многозначное число делится на 4, если две его последние цифры образуют число, делящееся на 4).
В результате изучения пункта учащиеся должны понимать термин «признак делимости», знать формулировки признаков делимости на 2, на 3, на 5, на 9, на 10 и уметь приводить иллюстрирующие их примеры; применять признаки для обоснования в ходе несложных рассуждений (см. упражнения 485, 486, 489, 491). Следует также показать учащимся, как признаки делимости «работают» при разложении числа на простые множители и предложить им удобную схему выполнения этого преобразования (см. упражнение 492).
Кроме того, полезно познакомить учащихся с иным, более компактным способом формулировки признаков делимости – заменой двух предложений с союзом « если…, то…» на одно, которое формулируется со словами «тогда и только тогда» или «в том или только том случае». Например: число делится на 5 в том и только том случае, когда оно оканчивается или цифрой 0, или цифрой 5.
Упражнения к пункту (и в группе А, и в группе Б) позволяют поддержать и развить знания, полученные ранее (свойства делимости, простые и составные числа, позиционный характер записи чисел в десятичной системе), а также продемонстрировать возможность получения других признаков делимости на базе уже изученных (см. упражнение 498). В сильном классе для желающих можно предложить эффектное задание, которое «аккумулирует» в себе все изученные признаки. Это задание таково: доказать, что число 2 438 195 760 делится на каждое из чисел от 2 до 18.
Прежде всего, следует обратить внимание на само число; оно десятизначное и для его записи использовать все 10 цифр. (Вот ещё примеры таких чисел, для которых можно выполнить то же задание: 3 785 942 160, 4 753 869 120, 4 876 391 520.)
На доске записывается данное число и под ним аккуратно записываются «цепочкой» все числа от 2 до 18 (в ходе доказательства числа не стираются и не вычёркиваются, так как с ними будет выполнена ещё дополнительная работа).
С помощью признаков делимости устанавливается, что данное число делится на 2, 3, 4, 5, 9, 10. (Заметим, что для этого, вообще говоря, достаточно установить факт делимости на 4, 9 и 10.)
Теперь ясно, что данное число делится на 6 (так как оно делится на 2 и на 3), делится на 12 (так как оно делится на 4 и на 3), делится на 15 (так как оно делится на 3 и на 5), делится на 18 (так как оно делится на 9 и на 2). Вопрос о том, являются ли делителями оставшиеся числа, можно решить непосредственным делением. (Заметим, что на 16 делить необязательно; достаточно разделить на 8 и убедиться, что в частном получается чётное число, или разделить на 4 и убедиться, что в частном опять получилось число, кратное 4.
Завершить работу можно таким заданием: «Укажите ещё какие-нибудь числа, на которые делится данное число». Делителями данного числа являются, например, произведения взаимно простых чисел, находящихся среди указанных делителей.)
Комментарий к упражнениям
490. а) Права Даша, так как число 158 не делится на 3.
491. Нужно вспомнить определение составного числа. Чтобы выполнить задание, достаточно в каждом случае указать один делитель числа, отличный от 1 и от самого числа.
493. Нужно подставлять такую цифру, чтобы сумма цифр получившегося числа делилась на 9.
а) Так как 3 + 1 + 8 = 12, то надо вместо звёздочки записать цифру 6. Никакая другая цифра не подходит.
б) Надо вписать цифру 7.
в) Имеем 4 + 8 + 2 + 5 = 19. Сумму цифр следует дополнить до 27. Подходит только цифра 8.
г) Так как 8 + 1 = 9, то подходят две цифры — это 0 и 9; задача имеет два ответа.
494. а) Сумма цифр числа 546 равна 15; ближайшая к ней сумма,
кратная 9, — это 18. Значит, к числу 546 надо прибавить 3. Получим 549.
497. Вспоминаем признаки, в которых вопрос о делимости решается по последней цифре. Приходим к выводу, что простое число не может оканчиваться цифрами 0, 2, 4, 5, 6, 8. Для приведения примеров можно использовать таблицу простых чисел.
498. 1) Надо сформулировать признак делимости на 6: число делится
на 6, если оно оканчивается чётной цифрой и сумма его цифр делится на 3.
2) Число делится на 45, если оно оканчивается цифрой 0 или цифрой 5 и сумма его цифр делится на 9.
Деление с остатком
Методический комментарий
С операцией деления с остатком учащиеся знакомы из курса начальной школы. В 5 классе этот материал необходимо повторить уже хотя бы потому, что соответствующие знания и умения потребуются при изучении обыкновенных дробей. Учащиеся узнают также некоторые новые аспекты данного вопроса, что позволит им расширить и углубить теоретические знания и развить практические умения.
Рассматривается вопрос о количестве остатков при делении на натуральное число n. При этом деление нацело рассматривается как частный случай деления с остатком, когда остаток равен 0. Обсуждается классификация натуральных чисел (разбиение на классы, на виды) по остаткам от деления: при делении на натуральное число n все натуральные числа разбиваются на n видов (дающие при делении на n остаток, равный 0, равный 1, …, равный n – 1).
В системе упражнений основное внимание уделено сюжетным задачам, для решения которых необходимо выполнить деление с остатком и дать содержательную интерпретацию полученного результата.
Комментарий к упражнениям
503. Можно проверить правильность ответа, выполнив деление.
506. 1) Так как 36 : 4 = 9, то в вагоне 9 купе.
2) Так как 20 : 4 = 5, то 20-е место находится в 5-м купе. Так как 25 : 4 = = 6 (ост. 1), то 25-е место находится в 7-м купе.
3) Так как ближайшее к 26 число, делящееся на 4, это 24, то в этом купе места начинаются с 25-го. Таким образом, в этом купе, кроме места под номером 26, находятся ещё 25-е, 27-е и 28-е места.
507. 1) Каждая пятёрка начинается с карточки белого цвета. Номер ка
