Аэродинамические характеристики самолета

Значения аэродинамических характеристик самолета определя­ются опытным путем в аэродинамических лабораториях, уточняют­ся в процессе летных испытаний и даются в виде графиков. Обычно даются графики зависимости коэффициента подъемной силы Су от угла атаки a и поляры самолета, выражающей зависимость коэф­фициента Су от коэффициента Сх самолета, т. е. Су=f(Сх).

На рис. 3 изображены графики аэродинамических характерис­тик самолета Ил-76Т при различной конфигурации, т. е. при раз­личном положении шасси и механизации крыла.

Аэродинамические характеристики самолета с убранным шасси и механизацией крыла для малых чисел М. По этим графикам на рис. 3 (кривые 1 и 1') можно определить:

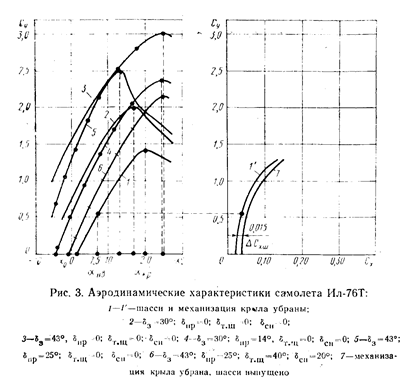
1. Аэродинамические характеристики самолета на каждом угле атаки. Для этого на оси абсцисс кривой Су==f(a) находим задан­ный угол атаки а, а на оси ординат — значение Су, на поляре — значение Су и Сх, соответствующие a. По значениям Су и Сх вы­числим аэродинамическое качество К=Су/Сх и угол качества

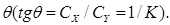
2. Точка пересечения кривой Су = f(a) с осью абсцисс даст зна­чение угла атаки нулевой подъемной силы a_о, который равен 1,5°. При этом угле атаки Су=0, К=0, а Сх₀=0,023=Сх_min. Как видим a_о положительный. Это объясняется тем, что за угол атаки самолета принимается угол атаки корневой части крыла. Известно, что крыло имеет геометрическую крутку Dj_кр = - 3°, при этом угол уста­новки корневой части крыла 3⁰, а в конце крыла 0°. Поэтому, если корневая часть крыла имеет угол атаки a_о= 1,5°, то концевая часть имеет a_о = -1,5°. Кроме того, при a_о =1,5° фюзеляж имеет отрица­тельный угол атаки (-1,5°), а на стабилизаторе также отрицательный, но больше по абсолютной величине. Следовательно, на a_о=1,5° корневая часть крыла создает положительную подъемную силу, а концевая часть крыла, фюзеляж и горизонтальное оперение создают такую же отрицательную подъемную силу. В результате Су=0 при a_о = 1,5°. Это явление справедливо и на других углах ата­ки. Поэтому необходимо всегда учитывать, что угол атаки в конце­вой части крыла на 3° меньше чем корневой.

3. Касательная к поляре, проведенная из начала координат, определяет в точке касания наивыгоднейший угол атаки a_нв, кото­рый равен 7,5⁰ (по корневой хорде крыла). На этом угле атаки К_max= 0,555/0,0358 = 15,5.

4. Проведя касательную к графикам параллельно оси абсцисс, определим величину Сy max =1,42 , которая соответствует критичес­кому углу атаки a_кр =20°.

5. Кривая Су=f(а) на значительном диапазоне углов атаки (до a =17 ... 18°) представляет почти прямую. Это указывает на то, что Сy возрастает пропорционально увеличению угла атаки. При углах атаки более 17 ... 18° рост Су замедляется. Это объяс­няется тем, что начиная с углов атаки 18⁰ нарушается плавность обтекания по задней кромке крыла. Наличие вихрей на верхней поверхности профиля вызывает некоторое уменьшение средней ве­личины разрежения над крылом. Вихреобразование в полете со­провождается появлением слабой тряски, которая с дальнейшим увеличением углов атаки усиливается. Появление тряски преду­преждает пилота о выходе самолета на углы атаки, близкие к критическому.

Для обеспечения безопасности полета необходимо знать срывные углы атаки и соответствующие им приборные скорости, при которых возможна потеря равновесия самолета.

Аэродинамические характеристики самолета при различных чис­лах М. Самолет Ил-76Т имеет ограничения максимальной скорости полета по числу М= 0,77. Эти ограничения вызвать прежде всего ненормальной работой крыла и хвостового оперения на больших числах М. Так, при числах М>Мкр, происходит смешанное обтека­ние крыльевых профилей, т. е. на профиле крыла имеет место до­звуковое обтекание, звуковое и образуются местные сверхзвуковые зоны, которые заканчиваются скачками давления. Сверхзвуковые зоны обтекания характеризуются значительными разрежениями воздуха, в результате чего при смешанном обтекании крыльевых профилей значительно изменяется картина распределения давле­ния по профилю и как следствие изменяется величина аэродина­мических характеристик, характеристик устойчивости и управляе­мости, возникают вибрации самолета. Большинство из этих явле­ний представляют большую опасность для полета. Для выяснения этих явлений в полете необходимо рассмотреть работу крыла на различных числах М. Для этой цели следует напомнить рад общих положений из аэродинамики больших скоростей.

1. Уравнение состояния газа. Состояние всякого газа характе­ризуется его плотностью, температурой и давлением.

Зависимость между статическим давлением газа, его плотностью и абсолютной температурой выражается уравнением состояния идеального газа

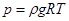
где р — статическое давление газа, кгс/м, r— массовая плотность газа в кгс-с²/м⁴, R — постоянная величина, называемая газовой постоянной кгс м /кгс град. Газовая постоянная определяется опытным путем: для воздуха R =29,27 кгс м/кгс град ; Т — абсолютная температура газа.

Из уравнения видно, что величина статического давления газа находится в прямой зависимости от его плотности, абсолютной тем­пературы и газовой постоянной.

2. Звук, скорость звука и число М. В воздухе, как и в упру­гой среде, колебания распространяются в виде продольных волн. В процессе звуковых колебаний происходит сжатие и расширение воздуха. Учитывая высокую частоту колебаний, процесс сжатия и расширения воздуха можно считать адиабатическим. Следователь­но, в процессе распространения звука плотность, температура и давление воздуха изменяются по адиабатическому закону. Ско­рость, с которой распространяются малые изменения давления, а значит и плотности воздуха, называется скоростью звука.

Скорость распространения звука в любом газе может быть определена по формуле: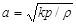

Подставив значение р в формулу, получим

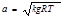где: для воздуха k=1,4; g==9,81 м/с². Подставив эти значения, получим скорость звука в воздухе а» 20,1 ÖТ м/с.

Скорость звука в любом газе зависит от природы газа, так как k и R для разных газов различны. Кроме того, скорость звука на­ходится в прямой зависимости от абсолютной температуры. При большей температуре скорость движения молекул воздуха и его упругость больше, поэтому процесс сжатия распространяется с большей скоростью. При t=15°С, T=288К, а=340,4м/с² »1225 км/ч.

С поднятием на высоту температура воздуха понижается на каждые 1000 м высоты на 6,5° С; вследствие чего скорость звука уменьшается в среднем на 4 м/с. На высотах от 11 000 до 25 000 м температура воздуха не изменяется, следовательно, скорость звука остается постоянной. На Н=11000 ... 25000 м, t=— 56,5°С, Т=216,5К а=292,2 м/с » 1063 км/ч.

Скорость звука связана со сжимаемостью воздуха, поэтому она может служить критерием при оценке влияния сжимаемости воз­духа па полет самолета с большими скоростями. Влияние сжимае­мости воздуха на аэродинамические и летные характеристики само­лета зависит от того, насколько скорость полета самолета близка к скорости звука. Многие явления в полете, в том числе и небезо­пасные (ухудшение устойчивости и управляемости, вибрация само­лета и т. п.), зависят от сжимаемости воздуха, а следовательно, и от скорости звука. Поэтому экипажу самолета необходимо точно знать, как близка скорость полета самолета к скорости звука. Приборы, которые замеряют приборную и истинную скорости, определить близость скорости полета к скорости звука не могут, так как скорость звука в воздухе непостоянна. Следовательно, для контроля полета необходимо иметь прибор, который мог бы точно определить, как близка скорость полета к скорости звука. Таким прибором является указатель числа М.

Число М выражается отношением истинной скорости полета к скорости звука, т. е. М=V/а. Из этого определения следует, что дозвуковой полет характеризуется числом М<1, звуковой М=1, а сверхзвуковой М>1. Большинство современных транспортных. самолетов являются дозвуковыми и имеют ограничения по чис­лу М.

Для самолета Ил-76Т для всех элементов полета, включая и экстренное снижение, максимально допустимое число М равно 0,77.

3. Закон постоянства расхода воздуха в струйке. Закон посто­янства расхода — это закон сохранения количества (массы) ве­щества в газовых (воздушных) струйках. Количество воздуха, про­ходящего за одну секунду через любое сечение струйки, зависит от его плотности р, площади сечения S и скорости течения V.

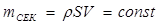Таким образом, постоянство секундной массы воздуха, проходя­щей через любое сечение струйки, можно записать уравнением

Практическое значение уравнения постоянства расхода заклю­чается в том, что оно устанавливает связь между скоростью и се­чением струйки.

4. Закон Бернулли. Закон Бернулли выражает зависимость меж­ду давлением и скоростью в любой точке установившегося воздуш­ного потока.

В установившемся потоке молекулы воздуха имеют два вида движений: тепловое (беспорядочное) и поступательное в направ­лении потока. В результате теплового движения молекул возника­ет статическое давление р=rgКТ. В результате поступательного движения молекул воздушный поток создает динамическое давление (скоростной напор), которое может быть выражено фор­мулой q=rV²/2.

На основании закона сохранения энергии в изолированной струйке сумма статического давления р и динамического давле­ния есть величина постоянная, т. е. p + rV²/2=const .

Это уравнение устанавливает связь между статическим давле­нием и скоростью в струйке и носит название уравнения Бернулли (для малых чисел М). Из уравнения Бернулли видно, что увеличе­ние скорости потока и его кинетической энергии возможно только вследствие уменьшения статического давления.

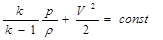Если течение воздуха происходит при числах М>0,4, то при из­менении сечения изолированной струйки воздух адиабатически сжи­мается, а его плотность, температура и внутренняя энергия изме­няются. Поэтому связь между давлением и скоростью, выраженная предыдущим уравнением, будет неточной. Уравнение Бернулли для больших чисел М

где k — показатель адиабаты.

Коэффициент k(k—1) в первом слагаемом вводит поправку в зависимость между скоростью и давлением в сжимаемом потоке.

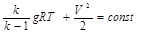Используя уравнение состояния газа, можно написать, что р/r=gRТ и заменив в первом слагаемом уравнения величину р/r на gRТ, получим следующее выражение уравнения Бернулли:

В этом виде уравнение Бернулли устанавливает связь между скоростью и температурой воздуха вдоль струйки сжимаемого по­тока.

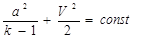Используя формулу для определения скорости звука а²=kgRТ, получим уравнение Бернулли, которое устанавливает связь между скоростью потока и скоростью звука в этом потоке

Из уравнения Бернулли для больших чисел М следует, что при ускорении воздушного потока в струйке кинетическая энергия уве­личивается, при этом воздух адиабатически расширяется, а его плотность р, температура Т, давление р=rgRТ и скорость звука а=20,1ÖT уменьшаются. И, наоборот, при торможении воздух адиабатически сжимается, его плотность, температура, давление и скорость звука в нем увеличиваются (кинетическая энергия пере­ходит в тепловую).

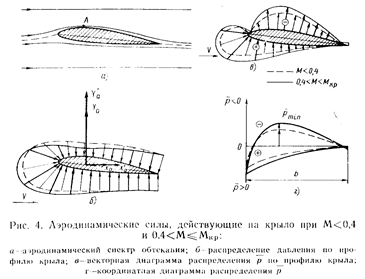
На основании закона постоянства расхода воздуха в струйке и закона Бернулли можно изучить особенности работы крыла и из­менение его аэродинамических характеристик при увеличении числа М. Рассмотрим аэродинамические силы крыла при малых числах М<0,4 (рис. 4).

На верхней поверхности профиля крыла, установленного под положительным углом атаки, сечения струек набегающего потока до точки профиля А постепенно уменьшаются, скорость течения увеличивается вследствие уменьшения статического давления (см. рис. 4, б). От точки А сечения струек постепенно увеличиваются, скорость потока уменьшается вследствие увеличения статического давления. В итоге на верхней поверхности крыла статическое дав­ление воздуха меньше давления в набегающем потоке.

Впереди крыла и под крылом сечение струек больше, скорость потока меньше, статическое давление больше давления в невозму­щенном потоке.

Такие явления наблюдаются в основном потоке (вне погранич­ного слоя).

Кроме основного потока, обтекающего профиль крыла, в не­посредственной близости к его поверхности имеется пограничный слой, в котором происходит относительное движение слоев, а значит, и проявляются силы вязкости (силы трения), приложенные к поверхности крыла, направленные по потоку (касательно поверх­ности профиля).

В результате неравномерного распределения давления по по­верхности крыла и сил трения в пограничном слое возникает аэро­динамическая сила Ra, которая приложена в центре давления крыла и направлена в сторону пониженного давления.

Так как при изменении углов атаки крыла давление на профи­ле перераспределяется, а величина, направление и точки прило­жения силы Ra изменяются, то силу Ra раскладывают на две сос­тавляющие, которые имеют постоянное направление.

Аэродинамическая подъемная сила Ya всегда направлена перпендикулярно к набегающему потоку (вектору скорости полета) в сторону пониженного давления и возникает вследствие разности давлений под крылом и над ним.

Сила лобового сопротивления Хa направлена параллельно на­бегающему потоку (параллельно вектору скорости полета, но в обратную сторону).

Сила лобового сопротивления возникает вследствие разности давлений впереди крыла и за ним, а также вследствие трения воз­духа в пограничном слое крыла.

Величина этих сил определяется соответственно по формулам:

Ya = Cya S r V²/2 Xa = Cxa S r V²/2

где q= r V²/2 — скоростной напор; Суa — коэффициент подъемной силы; Сха — коэффициент силы лобового сопротивления; S — площадь крыла, м²; r- плотность воздуха, кгс с²/м⁴; V — ско­рость полета (набегающего потока), м/с.

Коэффициенты Сya и Сха определяются опытным путем. Они соответственно учитывают зависимость Ya и Хa от угла атаки, его формы, состояния поверхности крыла и числа М (оно учитыва­ет влияние сжимаемости воздуха).

Коэффициент Суа зависит прежде всего от распределения дав­ления по профилю крыла, а коэффициент Сха кроме того, и состоя­ния поверхности крыла. В дальнейшем величины Уа, Хa, Сya. и Сха будут обозначаться соответственно У, X, Су и Сх, так как везде речь будет идти об аэродинамических силах и их коэффици­ентах, рассмотренных в скоростной системе координат ОХаУаZа (см. ГОСТ 20058-74).

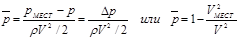Картину распределения давления по профилю удобно изобра­жать при помощи коэффициентов давления р с чертой (рис. 4, в, г). Если давление в невозмущенном потоке (вдали от профиля крыла) обоз­начим через р, а давление в какой-либо точке профиля — через р_мест, то разность р_мест - р=Dр выражает избыточное давление в данной точке профиля. Коэффициент давления определяется так:

Таким образом, коэффициент давления р выражается отноше­нием избыточного давления в данной точке профиля к динамичес­кому давлению невозмущенного потока.

Из определения коэффициента р (с чертой) видно, что если избыточное давление на крыле Dр растет пропорционально динамическому давлению r V²/2, то коэффициент р (с чертой) остается величиной постоянной.

Если в какой-либо точке профиля (например, под крылом при a>0) давление p_мест больше, чем давление р в невозмущенном по­токе, то избыточное давление Dр и коэффициент давления р поло­жительны (векторы на рис. 4, в направлены по нормали к контуру профиля). И, наоборот, если давление в точке профиля (над кры­лом при a>0) р_мест меньше давления р невозмущенного потока, то избыточное давление и коэффициент давления р отрицательны (век­торы направлены по нормали от контура профиля крыла).

Из выражения для коэффициента давления следует, что если при постоянном угле атаки крыла увеличить скорость набегающего потока, то пропорционально ей увеличиваются и все местные ско­рости на профиле, а это значит, что отношение V²_мест./V₂ и коэффициенты давления р останутся постоянными в каждой точке профи­ля. Следовательно, избыточные давления на профиле в этом слу­чае растут прямо пропорционально динамическому давлению не­возмущенного потока.

Пропорциональность между избыточным давлением Dр на про­филе крыла и динамическим давлением rV²/2 невозмущенного по­тока (постоянство коэффициентов р) при изменении скорости нару­шается при таких числах М, когда начинает сказывается сжимае­мость воздуха. Например, при числах М>0,4 в критической точке профиля крыла (передняя кромка) поток тормозится, воздух сжи­мается, его плотность увеличивается, а значит, увеличивается и ди­намическое давление по сравнению с динамическим давлением не­возмущенного потока. Это вызывает дополнительный прирост из­быточного давления и коэффициента давления р.

В тех точках профиля, где поток ускоряется, воздух расширяет­ся, его плотность, температура и давление уменьшаются. Это вызы­вает дополнительное ускорение потока, в результате которого соз­дается большее разрежение. Отрицательные избыточные давления по абсолютной величине возрастают быстрее, чем динамическое давление невозмущенного потока, а значит и отрицательные зна­чения коэффициентов давления по абсолютной величине увеличи­ваются.

Отложив в некотором масштабе величины коэффициента дав­ления по нормали, к контуру профиля, получим векторную диаграм­му распределения давления (см. рис. 4, в).

Можно построить также координатную диаграмму распределе­ния давления (см. рис. 4, г). В этом случае хорду профиля прини­мают за единицу и располагают по оси абсцисс, а коэффициент давления р откладывают по оси ординат. Отрицательные значения р откладывают вверх, а положительные — вниз.

На диаграммах рис. 4, в, г, распределение давления соответст­вует картине распределения давления, изображенной на рис. 4 б. По величине площади диаграммы коэффициентов давления можно судить о величине коэффициента Су. Избыточные давления под крылом и над ним можно заменить их средними значениями, со­ответственно Dp_н.ср и Dр_в.ср. Тогда подъемная сила крыла будет равна произведению разности средних избыточных давлений под крылом и над ним Dp_н.ср - Dр_в.ср на площадь крыла S

Y = (Dp_н.ср - Dр_в.ср)S

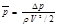Так как коэффициент давления:

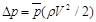то из этого выра­жения

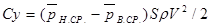а подъемная сила

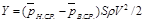Сравнивая формулы определения подъемной силы, видим, что

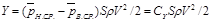Таким образом,

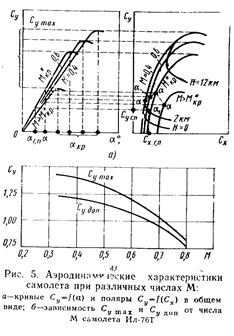
т. е. коэффициент подъемной силы Су — разность средних коэффициентов давления под крылом и над ним.

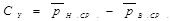Из выражения для Су видим, что он зависит от тех же факторов, что и разность средних коэффициентов дав­ления, т. е. от формы крыла, угла атаки и числа М.

Если изменить форму крыла или угол атаки, то изменятся местные давле­ния, избыточные давления и коэффициенты давления по крылу, а значит, изменятся и величины коэффициентов Су и Сх.

При числах М<0,4 сжи­маемость воздуха практиче­ски не влияет на картину распределения давления по профилю крыла, а значит избыточное давление Dр по профилю изменяется про­порционально скоростному напору rV²/2, величина коэффициентов давления р, а также коэффициентов Су и Сх на каждом угле атаки остается постоянной. Следовательно, положение графиков Су= f(a) и Су=f{Сх) в системе координат не изменится (рис. 5 при М<0,4). На рис. 4 картина распределения давления и коэф­фициентов давления р ограничена пунктирной линией.

Учитывая особенности течения воздуха при М>0,4, можно уста­новить особенности работы крыла при этих числах М. Картина распределения давления по профилю на рис. 4 ограничена контур­ной линией.

На верхней поверхности крыла, так же как и при малых чис­лах М поток ускоряется, но в процессе ускорения воздух адиаба­тически расширяется. Его плотность и температура значительно уменьшаются, вследствие чего более значительно уменьшаются местные давления. Впереди крыла и под ним поток тормозится, воздух адиабатически сжимается, его плотность, температура и давление повышаются в большей степени, чем при малых числах М.

Вследствие дополнительного понижения давления (разрежения) над крылом и дополнительного повышения давления под крылом, вызванного сжимаемостью воздуха, подъемная сила крыла увели­чивается. Дополнительное повышение давления впереди крыла и рост силы трения в пограничном слое вызывает увеличение лобового сопротивления. Подъемная сила и сила лобового сопротивления при этих числах М возрастают не пропорционально квадрату скорости, а в несколько большей степени, что учитывается увеличением коэффициентов подъемной силы Су и лобового сопротивления Сх.

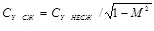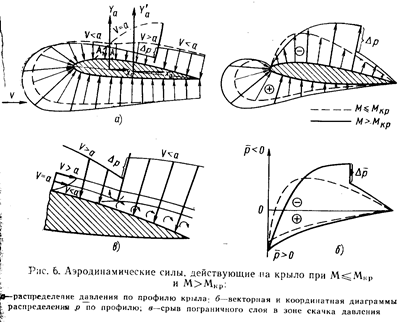
Величину коэффициента Су с учетом сжимаемости воздуха до Мкр приближенно можно определить по формуле

где Сy несж соответствует числам М=0,2 ... 0,3.

Так, если Су несж =0.4, то при М=0,7 получим Су сж= 0,56.

Подъемная сила при этих числах М растет пропорционально квадрату скорости и вследствие увеличения Су , вызванного сжимаемостью воздуха.

Сила лобового сопротивления увеличивается пропорционально квадрату скорости, а также вследствие увеличения коэффициен­та Сх.

Величина аэродинамического качества самолета несколько уменьшается. Рост коэффициентов Су и Сх в результате сжимае­мости воздуха вызывает смещение каждого угла атаки и самой поляры вверх и вправо, а кривая Су=f{а) увеличивает угол на­клона относительно оси абсцисс (см. рис. 5, М=0,6, Мкр со звездой и a).

Рост коэффициента Су на каждом угле атаки не означает, что при больших числах М растет и Су max. Наоборот, при числах М>>0,4 наблюдается уменьшение Сy max и Су тр вследствие уменьшения aкр и aтр. Критический угол атаки и угол атаки тряски в этом случае уменьшаются потому, что срыв потока на крыле начинает­ся на меньших углах атаки. Это можно объяснить следующим. На верхней поверхности профиля крыла воздух в процессе ускорения значительно расширяется, а давление понижается, затем воздух резко тормозится у задней поверхности профиля и давление резко возрастает. Большая разность давлений вызывает перемещение пограничного слоя воздуха от задней кромки вперед, вследствие чего он набухает и срывается в виде вихрей при меньших углах атаки.

Таким образом на больших числах М уменьшается критический угол атаки и величина Су max. Тряска самолета начинается также при меньших углах атаки и величина Су тр » Су доп уменьшается. Учитывая это, полет в неспокойном воздухе следует выполнять на меньших числах М, так как возможно резкое увеличение углов атаки.

Такие изменения в работе крыла и его аэродинамических ха­рактеристик наблюдаются до Мкр.

Пусть скорость набегающего потока на крыло, установленное под положительным углом атаки, меньше скорости звука в этом потоке (V<а). Поток в верхней части профиля ускоряется, его плотность, температура, давление и местная скорость звука умень­шаются. Одновременное увеличение скорости потока и уменьшение скорости звука в нем приводит к тому, что в определенной точке профиля (точке А на рис. 6) местная скорость потока становится равной местной скорости звука. Скорость набегающего потока (скорость полета) в этом случае называют скоростью волнового кризиса или критической. Число М, соответствующее этой скоро­сти, называется критическим Мкр.

Таким образом, число М полета, при котором впервые на поверхности обтекаемого тела (крыла, оперения и др.) хотя бы в од­ной точке возникает скорость потока, равная местной скорости зву­ка, называется критическим.

Например, на высоте 10000 м t=-50°С (Т=223К) скорость звука а=1078 км/ч. Если при скорости полета 755 км/ч на профи­ле крыла будет достигнута местная скорость звука, то Мкр=V/а = 755/1078 = 0,7.

На рис. 6 точка А, в которой впервые местная скорость потока достигает скорости звука, находится в верхней части профиля, где местная скорость потока максимальная, а давление и коэффици­ент давления минимальные. На координатной диаграмме распре­деления давления точка, соответствующая минимальному значе­нию коэффициента давления (максимальному разрежению) на профиле, отмечена р_min, (см. рис. 4,г).

Рассмотрим аэродинамические силы и характеристики профиля крыла на числах М>Мкр.

На рис. 6 показано распределение давления по профилю в ус­ловиях обтекания крыла потоком при Мкр и числах М>Мкр.

При Мкр только в одной точке профиля крыла была достигнута потоком местная скорость звука. Наличие звуковой скорости в од­ной точке потока не изменяет величины местных скоростей и давле­ний по профилю крыла. Следовательно, при Мкр крыло работает так же, как и при числе М, несколько меньшем Мкр.

Если число М невозмущенного потока становится значительно больше Мкр, то наступает режим смешанного обтекания, т. е. наря­ду с дозвуковыми и звуковыми местными скоростями на профиле появляются и сверхзвуковые.

Поток, обтекающий верхнюю поверхность крыла, в передней части профиля будет дозвуковым (на рис. 6 дозвуковая зона пото­ка отмечена V<а). По мере набегания на профиль поток ускоря­ется вследствие уменьшения сечения струек. В процессе ускорения происходит адиабатическое расширение воздуха. Его плотность, температура, давление и скорость звука уменьшаются. В той ли­нии тока, где при Мкр) была впервые достигнута местная скорость звука (точка А), при числах М>Мкр, она достигается несколько ближе к передней кромке крыла (точка А₁). Это объясняется тем, что при увеличении числа М за Мкр все местные скорости потока на профиле увеличились, а местные скорости звука уменьшились. Такое изменение местных скоростей потока и скоростей звука обес­печивает достижение потоком местных скоростей звука и в линиях тока, находящихся на некотором расстоянии от поверхности крыла, только несколько дальше от передней кромки (см. штриховую ли­нию на рис. 6 а, где V=а). Это объясняется тем, что в этой части потока сечение струек несколько больше, чем в непосредственной близости к профилю. Поэтому для достижения потоком местных звуковых скоростей требуется дополнительное ускорение, которое происходит вследствие дальнейшего уменьшения сечения струек над передней половиной профиля крыла.

Поток, достигший местной скорости звука, продолжает уско­ряться и становится сверхзвуковым. Ускорению потока (переходу через скорость звука) способствует выпуклость верхней поверх­ности профиля. Благодаря этому сечение струек, особенно над зад­ней половиной профиля, увеличивается. Воздух в процессе ускоре­ния над задней половиной профиля продолжает адиабатически рас­ширяться, а его плотность, температура и давление падать. Сни­жение давления и способствует ускорению сверхзвукового потока.

Таким образом, на профиле крыла появляется сверхзвуковая зона (на рис. 6 а она отмечена V>а). Так как невозмущенный по­ток воздуха далеко впереди крыла дозвуковой и, кроме того, сече­ния струек и всего потока впереди крыла и за ним практически одинаковые, то скорость и давление также одинаковы. Следова­тельно, за профилем крыла поток также дозвуковой, а давление в нем значительно больше, чем в сверхзвуковой зоне на профиле крыла.

Поток сверхзвуковой зоны, встречая значительное противодавление потока за профилем крыла, начинает тормозиться. В процессе торможения сверхзвукового потока происходит мгновенное сжатие воздуха. Плотность, температура, давление и местная скорость звука скачкообразно возрастают, а скорость потока также скачкообразно уменьшается и становится дозвуковой. Скачкообразный рост давления и вызывает скачкообразное уменьшение скорости потока. Таким образом, вследствие торможения сверхзвуко­вого потока на профиле крыла возникает прямой скачок уплотне­ния, замыкающий сверхзвуковую зону. Давление за скачком уплот­нения резко увеличивается, но не достигает той величины, которая была при Мкр, когда не было сверхзвуковой зоны со скачком уп­лотнения. Это видно и на диаграмме распределения давления (см. рис. 6 б), где векторы р (с чертой) за скачком оказались большими, чем при Мкр. Такое изменение давления и его коэффициентов подтвержда­ет то, что в скачке уплотнения протекает необратимый процесс сжатия воздуха, при котором часть тепловой энергии в скачке рассеивается, а значит давление и коэффициент давления р пол­ностью восстановиться не могут.

Если профиль крыла симметричный, то при a=0 процессы об­разования сверхзвуковых зон со скачками уплотнения возникают одновременно на верхней и нижней поверхностях профиля. Если же профиль крыла несимметричный или же симметричный профиль расположен под положительным углом атаки, то на нижней по­верхности крыла появление сверхзвуковых зон со скачками уплот­нения происходит при несколько большем числе М.

Следует обратить внимание на то, что при М>Мкр размеры сверхзвуковой зоны на профиле крыла увеличиваются по мере увеличения числа М. Это объясняется тем, что при больших чис­лах М поток достигает местных скоростей звука ближе к передней кромке и на большем расстоянии от профиля. Следовательно, боль­шая масса воздуха приобретает сверхзвуковую скорость и ее торможение начинается ближе к задней кромке профиля, т. е. скачок уплотнения смещается назад. Эти явления наблюдаются в верхней и нижней сверхзвуковых зонах. При числах М, близких к единице, скачки уплотнения, замыкающие сверхзвуковые зоны, смещаются к задней кромке крыла.

Наличие сверхзвуковых зон со скачками уплотнения на крыле совершенно по другому распределяет давление по профилю. Вслед­ствие этого изменяется величина аэродинамических сил и переме­щается точка приложения их по хорде, а следовательно, изменя­ются и аэродинамические характеристики профиля крыла.

Появление и развитие местных сверхзвуковых зон со скачками уплотнения на профиле крыла, приводящее к резкому изменению его аэродинамических характеристик, получило название волново­го кризиса крыла.

Характер изменения коэффициента Су при М>Мкр на положи­тельных углах атаки крыла определяется в основном следующими явлениями, характеризующими работу крыла.

1. При М>Мкр в дозвуковых зонах потока на профиле крыла наблюдаются те же явления, что и при М<Мкр, т. е. на верхней поверхности увеличивается разрежение, что способствует увеличе­нию коэффициента Су (см. рис. 6 а, б).

2. При М>Мкр развивается сверхзвуковая зона на верхней по­верхности, в которой воздух продолжает ускоряться и расширять­ся. Расширение воздуха вызывает значительное понижение давле­ния вследствие уменьшения его плотности и температуры, а следо­вательно, рост разрежения. Это способствует увеличению Су.

3. В скачке уплотнения при сжатии воздуха происходит необ­ратимый процесс, часть тепловой энергии потока рассеивается, по­этому за скачком давление оказывается меньшим, чем на докритических числах М, что способствует увеличению коэффициента Су.

Таким образом, некоторое увеличение коэффициента Су после Мкр до числа М^*кр, происходит вследствие перечисленных явлений.

4. Вслед за появлением сверхзвуковой зоны со скачком уплот­нения на верхней поверхности при числе М, несколько большем Мкр, начинает появляться и развиваться сверхзвуковая зона со скачком уплотнения на нижней поверхности, причем обычно не­сколько ближе к задней кромке крыла. Эта зона характеризуется значительным разрежением воздуха, а значит и сильным уменьше­нием плотности, температуры и давления (особенно на малых уг­лах атаки). Значительное падение давления в этой зоне является причиной уменьшения коэффициента Су после М*кр. Уменьшение Су называется срывом потока за скачком—волновым срывом.

Такое изменение коэффициента Су после Мкр оказывает сущест­венное влияние на величину подъемной силы. Так, до М*кр подъем­ная сила продолжает увеличиваться пропорционально квадрату скорости и вследствие роста Су. После М*кр Су резко уменьшается и подъемная сила крыла также уменьшается, хотя число М (ско­рость полета) возрастает. Появление и развитие сверхзвуковых зон со скачками уплотнения на верхней и нижней поверхностях профиля при М>Мкр вызывает резкое увеличение коэффициента Сх. Увеличение коэффициента Сх на этих числах М определяется следующими причинами.

1. У передней кромки профиля происходит процесс сжатия воздуха, вследствие которого величина коэффициентов давления р увеличивается, что способствует увеличению и коэффициента Сх.

2. Появление и развитие сверхзвуковых зон вызывает увеличе­ние разрежения на задней половине профиля, что способствует увеличению коэффициента Сх, причем на больших числах М сверх­звуковые зоны разрежения охватывают более задние участки про­филя, поэтому разность величин коэффициентов давления впереди профиля и за ним резко возрастает. Это вызывает более значитель­ный рост и коэффициента Сх.

3. Так как в скачке уплотнения происходит необратимый про­цесс сжатия воздуха, то величина давления за скачком оказывает­ся несколько меньше, чем на докритических числах М. Это также способствует некоторому увеличению Сх.

4. Немалую роль в росте коэффициента Сх может играть также волновой срыв пограничного слоя (см. рис. 6 в). Срыв пограничного слоя связан с тем, что скачок уплотнения начинается не на самой поверхности профиля (непосредственно у поверхности ско­рости течения пограничного слоя дозвуковые). Следовательно скачок уплотнения начинается на некотором (малом) расстоянии от поверхности профиля, где пограничный слой становится звуко­вым. Следует помнить, что пограничный слой воздуха всегда стре­мится перемещаться из области высокого давления в область низ­кого. Так как давление на профиле постепенно понижается от пе­редней кромки до скачка уплотнения, то пограничный слой на этом участке перемещается в направлении основного потока. За скач­ком уплотнения давление в основном потоке и пограничном слое значительно больше, чем перед скачком в сверхзвуковой зоне. Вследствие такой разности давлений пограничный слой от задней кромки профиля перемещается под скачком уплотнения в сверх­звуковую зону. Такое течение вызывает утолщение пограничного слоя и отрыв его от поверхности крыла перед скачком уплотнения. Вихри, возникающие в зоне срыва, сносятся потоком и постепенн