Вероятностные сетевые модели
ВЕРОЯТНОСТНЫЕ СЕТЕВЫЕ МОДЕЛИ
Выпускная квалификационная работа
| Обучающегося | 4 курса |
| Направления подготовки | 01.03.04 Прикладная математика |
| Форма обучения | очная |
| Научный руководитель доцент кафедры информатики, кандидат физико-математических наук, доцент | Л.И. Руденко |
| К ЗАЩИТЕ ДОПУСКАЮ: Заведующий кафедрой прикладной математики, доктор физико-математических наук, | В.Н. Чехов |
Симферополь, 2017
Аннотация
Мартынюк Д. С.Вероятностные сетевые модели. Выпускная квалификационная работа бакалавра по направлению подготовки 01.03.04 Прикладная математика. Таврическая академия Крымского федерального университета имени В. И. Вернадского.
Работа посвящена анализу методов математического моделирования задач управления проектами и использованию альтернативных сетевых моделей в прикладных задачах.
Ключевые слова: управление проектами, сетевые модели, альтернативные сетевые модели.
Страниц – 51, таблиц – 25, иллюстраций – 25, приложений – 1, библиографических источников – 25.
Оглавление
Введение. 4
1. Управление проектами и сетевые модели. 6
1.1. Основные этапы развития сетевых технологий. 6
1.2. Основные понятия проектного управления. 8
1.3. Структурная декомпозиция работ. 10
1.4. Сетевое планирование и управление. 12
1.4.1. Классификация сетевых моделей. 13
1.4.2. Детерминированная модель. 15
1.4.3. Вероятностная модель. 22
1.4.4. Альтернативные сетевые модели. 25
1.5. Выводы.. 30
2. Прикладные задачи с использованием альтернативных сетевых моделей. 31
2.1. Задача анализа времени производственного процесса. 31
2.2. Задача разработки оборудования для высокотемпературных систем.. 35
2.3. Задача выполнения научно-исследовательской работы.. 41
Заключение. 47
Список литературы.. 48
Приложение. 50
Введение
Разработка и внедрение в производство сетевых моделей начинается в середине XX столетия. Потребность в реализации масштабных проектов с привлечением большого количества материальных и трудовых ресурсов вызвала необходимость в использовании проектного подхода, моделирования. Это стало возможным благодаря развитию вычислительной техники. В конце 50-х в США были разработаны методы сетевого планирования и управления, такие как диаграмма Гантта (Gantt chart), CPM (Critical Path Method – Метод определения критического пути), PERT (Program Evaluation and Review Technique – техника оценки и анализа проектов), ставшие основой современных методик. Широкое внедрение ЭВМ поспособствовало развитию методов управления проектами (Project Management). В настоящее время управление проектами с использованием сетевых моделей применяется во многих сферах деятельности. Существует множество настольных программных комплексов и приложений с web‑интерфейсом, обладающих широкой функциональностью.
Несмотря на широкое распространение и внедрение в практику электронных систем управления проектами, знание теоретических основ разработки оптимизации и применения сетевых моделей остается актуальным и в настоящее время, позволяя правильно интерпретировать и анализировать результаты расчетов моделей, выполненных машинами. В особенности это относится к классу альтернативных моделей, в которых заранее не задана топология сети, а временные параметры имеют вероятностный характер. Тем более, что программное обеспечение, позволяющее строить и управлять проектами, основанными на данных моделях, не имеет широкого распространения.
Целью работы является изучение вероятностных сетевых моделей и особенностей их применения в решении практических задач управления.
Основные задачи работы включают:
- анализ основных типов вероятностных моделей на основе описания, сравнения, формализации, классификации;
- освоение математического аппарата расчета временных параметров в сетях различных типов;
- исследование альтернативных сетевых моделей и методов их построения и оптимизации;
- построение альтернативных сетевых моделей для задач управления.
Работа включает два раздела. В первом разделе проведен обзор и анализ методов сетевого планирования в применении к задачам управления проектами, рассмотрено математическое обоснование и имеющиеся программные средства. Все приведенные формулы и типы графических средств используются в прикладной части работы. Особое внимание уделено альтернативным сетевым моделям. Получены некоторые выводы о современном состоянии теории сетевого планирования и управления, а также о программных приложениях.
Во втором разделе рассмотрен ряд примеров использования сетевых моделей в прикладных задачах анализа и управления проектами (производством). В их числе два примера выполнены на основе задач, найденных в литературных источниках, а третий пример представляет сформулированную нами задачу анализа научно-исследовательского проекта на основе сетевых моделей разных типов. Проведены подробные вычисления, представленные в тексте работы и в Приложении. Получены сравнительные выводы о применении к данной задаче разных типов моделей. Выявлена необходимость в автоматизации процесса оптимизации вероятностной и альтернативной сетевой модели.
Основные понятия проектного управления
Одно из наиболее общих определений термина «проект» приводится в [2]: «проект – это ограниченное по времени и специально организованное, целенаправленное изменение отдельной системы в рамках запланированных ресурсов и установленных требований к качеству результатов». Автор отмечает, что проект отличается от производства своей уникальностью, а понятия «целенаправленное изменение» и «отдельная система» характеризует проект как целостную структуру, обособленную от иных проектов и предприятий. Однако производство обладает схожими характеристиками, а методология управления производством имеет общие черты с управлением проектами.
Любой проект в некоторой степени обладает ограниченностью, которую называют «тройственной». Это понятие опирается на три важнейших параметра проекта: время, стоимость и объём выполняемых работ. В этом ключе проект рассматривается как задача оптимизации с тремя основными ограничениями, где целевая функция — качество реализации [3, 13].
Проект имеет жизненный цикл, то есть набор определённых этапов, которые он проходит в зависимости от направленности и методов контроля. Основные (обобщенные) фазы жизненного цикла проекта представлены на Рис. 1.1.
Рис. 1.1. Фазы жизненного цикла проекта.
Проекты можно классифицировать по многим характеристикам, например, по масштабу, срокам реализации, сложности, причине возникновения и другим параметрам [2, 10, 11, 13]. В частности, по основным сферам деятельности различают такие типы проектов:
- социальные;
- экономические;
- организационные;
- технические;
- смешанные.
Классификация проектов полезна при выборе методов планирования, выделении главных целей и параметров, построении взаимосвязей между участниками проекта.
Однако проект не может существовать сам по себе. Разработка, реализации и последующий анализ осуществляют с помощью методов управления проектом. УП часто рассматривается в двух плоскостях:
- как форма воздействия на социально-экономическую систему;
- управление проектом в процессе формирования его результатов [6].
В [9, с. 107] представлена классификация проектного управления по конченой цели и внутреннему наполнению проекта (Таблица 1.1), хотя авторы подчёркивают, что любая классификация проектов, как и систем, носит весьма условный характер.
Таблица 1.1.
| Классификация проектного управления. | |||
| Содержание | |||
| Неограниченное | Ограниченное | ||
| Цель | Терминальная | Мультипроектное управление | Терминальный проект |
| Нетерминальная | Открытый проект | Развивающийся проект |
С другой стороны, в [6] представлено чёткое структурирование целей по типам, а именно:
- требуемое конечное состояние проектируемой системы (монопроект);
- требуемый порядок смены состояний – программа движения (мультипроект);
- требуемое направление движения системы без фиксации конечной точки (мегапроект).
Несмотря на различия в терминологии, группировка проектов по целям имеет общие черты с классами проектного управления по [14].
Участниками проекта называются юридические или физические лица, которые или непосредственно участвуют в его реализации, или их интересы могут быть затронуты по мере его осуществления [2]. Очевидно, что в простых проектах участие может принимать и одно лицо, тогда как в комплексных набор участников может включать в себя множество компаний, органы власти, частные лица и т.д.
Всех участников проекта можно разделить на категории:
- управленческий аппарат заказчика проекта;
- управленческий аппарат исполнителя проекта;
- команды проектов [3].
Внешняя среда по отношению к проекту называется окружением проекта. Окружение проекта способно оказывать значительное влияние как на сам проект, так и на его организаторов, и служит источником рисков.
Методология, то есть совокупность правил и методов, должна определять конкретные составляющие для эффективного осуществления проекта. Существует много методологий управления проектом, в том числе:
- каскадная или «классический проектный менеджмент» – предполагает неизменность базовых задач;
- PERT-оценка продолжительности работ и PERT/COST-анализ материальных затрат;
- МКП – наглядный способ календарного планирования;
- PRINCE2 (стандарт УП в Великобритании);
- RWP (планирование методом набегающей волны);
- LEAN (от. англ. «бережливый») – концентрация на устранении потерь.
Детерминированная модель
Будем вначале рассматривать детерминированные сетевые модели. Построение любой сетевой модели начинается с определения списка работ (событий) и построения логической взаимосвязи между ними. Если модель не имеет каких-либо числовых показателей и обозначений, она называется структурной сетевой моделью или топологией [14]. После определения топологии происходит оценка аналитических параметров (продолжительности работ, потребностей в ресурсах и др.). Затем проводится анализ и оптимизация модели.
Приведем требования к одноцелевой СМ с одним исходным событием:
- узлы пронумерованы в порядке выполнения, т. е. для каждой дуги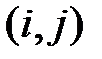 
;
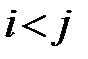- отсутствуют тупиковые узлы (кроме завершающего), т. е. такие, за которыми не следует хотя бы одна дуга;
- отсутствуют узлы (за исключением исходного), которым не предшествует хотя бы одна дуга;
- отсутствуют циклы, т. е. замкнутые цепи, соединяющие узел с ним же самим [20];
- между смежными узлами может проходить только одна дуга;
- узлы строят последовательно (стрелки направлены слева направо – от начала к окончанию);
- следует избегать пересечения дуг на графике;
- фиктивные работы обозначаются пунктирной линией.
Перед построением сетевой модели технологическую последовательность работ заносят в таблицу (
Таблица 1.3).
Таблица 1.3.
| Технологическая последовательность работ. | |
Предшествующие работы ( 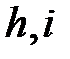 ) | Данные работы (  ) |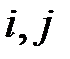
| — | 0,1 |
| 0,2 | |
| 0,3 | |
| 0,1 | 1,4 |
| 0,1 | 2,5 |
| 0,1 | 2,6 |
| 0,1 | 3,6 |
| 1,4 | 4,7 |
| 2,5 | 5,7 |
| 2,6 3,6 | 6,8 |
| 4,7 5,7 | 7,8 |
Построенный по этой таблице сетевой график приведён на
Рис. 1.4.
Рис. 1.4. Сетевой график типа «узел – событие».
Так как сеть – это ориентированный граф, который определяется через бинарное отношение, он также однозначно определяется через матрицы инцидентности [19]. А поскольку работы упорядочены во времени, и дуга связи всегда идёт от события с меньшим номером к событию с большим номером, то достаточно определить матрицу смежности. Расчёт временных и других параметров в компьютерных системах требует табличного или матричного представления проекта. Например, для описанной выше сетевой модели матричное представление выглядит так (Таблица 1.4):
Таблица 1.4.
| Матрица сетевого графика. | |||||||||
| События | |||||||||
Количество столбцов и строк в матрице равно количеству событий. Каждый столбец и строка нумеруются по порядку согласно количеству событий. Затем на пересечении каждой строки, соответствующей начальному событию, и столбцу, соответствующему последующему событию, ставится «1», а во всех остальных случаях – «0».
Наряду с понятиями работ и событий в сетевом моделировании очень важным является понятие пути.
Путь – это непрерывная последовательность работ между двумя событиям сети. Не каждая пара вершин имеет связывающий их путь.
Полный путь – это непрерывная последовательность работ между исходным и завершающим событием сетевой модели. Суммарная продолжительность работ, лежащих на пути, определяет длину пути [14]. Таких путей в сетевой модели может быть несколько.
Критический путь – это полный путь, длина которого максимальна. В модели может быть несколько критических путей, включающих разные последовательности работ. Примем следующие обозначения для аналитических параметров (Таблица 1.5).
Таблица 1.5.
| Аналитические параметры сетевой модели. | ||
| № п/п | Название параметра | Условное обозначение |
| Код данной работы | i,j | |
| Код начального события данной работы | i | |
| Код конечного события данной работы | j | |
| Код работы, предшествующей данной | h,i | |
| Код события, предшествующего работе (i,j) | h | |
| Код работы, следующей за конечным событием данной работы | j,k | |
| Код события, следующего за работой j,k | k | |
| Путь | L | |
| Продолжительность пути | TL | |
| Критический путь | Lкр | |
| Продолжительность критического пути | TLкр | |
| Продолжительность данной работы | tij | |
| Раннее начало данной работы |  | |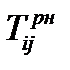
| Раннее окончание данной работы |  | |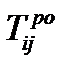
| Позднее начало данной работы |  | |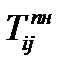
| Позднее окончание данной работы |  | |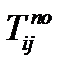
| Общий (полный) резерв времени данной работы |  | |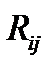
| Свободный резерв времени данной работы |  |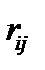
Учитывая время выполнения работы,
Таблица 1.3 дополняется ещё одним столбцом под названием «Продолжительность» (Таблица 1.6).
Ниже представлены графики с временной характеристикой. На Рис. 1.5. Сетевая модель «узел – событие» с изображена модель «узел – событие» (работы на дугах, AoA) с указанием времени выполнения работ.
Таблица 1.6.
| Технологическая последовательность работ с учетом продолжительности. | ||
| Предшествующие работы ( 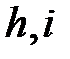) | Данная работа ( 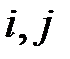) | Продолжительность  |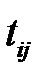
| — | 0,1 | |
| 0,2 | ||
| 0,3 | ||
| 0,1 | 1,4 | |
| 0,1 | 2,5 | |
| 0,1 | 2,6 | |
| 0,1 | 3,6 | |
| 1,4 | 4,7 | |
| 2,5 | 5,7 | |
| 2,6 3,6 | 6,8 | |
| 4,7 5,7 | 7,8 |
Рис. 1.5. Сетевая модель «узел – событие» с указанием временных параметров.
Модель «узел – работа» (AoN) имеет существенные отличия от предыдущей. В узле содержится следующая информация (Рис. 1.6).
Рис. 1.6. Параметры, описываемые в узле модели «узел – работа».
На Рис. 1.7 представлена модель «узел – работа», эквивалентная изображённой на Рис. 1.5.
Рис. 1.7. Сетевая модель «узел – работа» с временными параметрами.
Особенностью построения СМ «узел – работа» являются:
- добавление условных узлов «Начало», предшествующего всем узлам и «Окончание», следующего после всех работ (работы в этих узлах имеют нулевую продолжительность);
- работы можно нумеровать одним индексом;
- нет необходимости вводить фиктивные события, обозначающие логическую взаимосвязь событий;
- вычисление аналитических параметров удобно проводить прямо на графике.
Временные параметры работ и событий определяются на основе метода динамического программирования.
Ранние начало работ (время, раньше которого событие наступить не может) определяется последовательно от начального события до конечного. Для работ, выходящих из начального события, раннее начало равно нулю. Чтобы посчитать раннее начало последующих работ, необходимо определить раннее окончание работ, начинающихся от исходного. Раннее окончание вычисляется по формуле
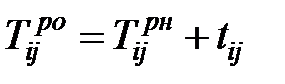 . | (1.1) |
Раннее начало данной работы равно максимальному из ранних окончаний предшествующих:
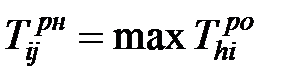 . | (1.2) |
Позднее начало и позднее окончание работы вычисляются в обратном порядке, причём поздние окончания работ, предшествующих заключительному событию(работу) выбираются как максимальное раннее окончание из этих работ. Позже этого времени ни одна работа не закончится. Позднее начало работы можно вычислить по формуле
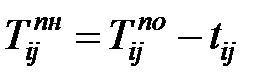 , | (1.3) |
а позднее окончание предшествующей работы всегда равняется минимуму из поздних начал последующих:
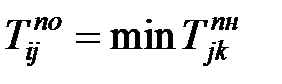 | (1.4) |
Критическими называются работы, лежащие на критическом пути. Для них обязательно выполнение следующих свойств.
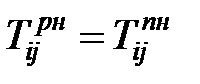 , | (1.5) |
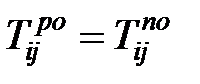 . | (1.6) |
То есть полный резерв времени работ, который можно вычислить по любой из двух формул
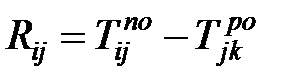 , | (1.7) |
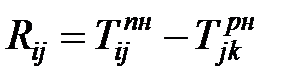 , | (1.8) |
для критических работ будет равен нулю.
Для остальных работ полный резерв означает, что можно увеличить её длительность или начать работу позже. Полный резерв принадлежит не конкретной работе, а всему пути, содержащему эту работу. Поэтому логично, что для любого пути, не являющегося критическим, вводится понятие общего (полного) резерва времени, который будет равен разнице между длиной критического и данного пути:
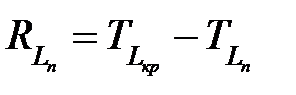 . | (1.9) |
Частный (свободный) резерв определяет, на сколько можно сдвинуть работу или увеличить её длительность, чтобы не повлиять на раннее начало других работ и общие резервы всех последующих работ, которые находятся на том же пути, что и данная. Частный резерв вычисляется по формуле
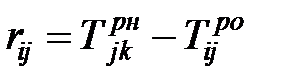 . | (1.10) |
Независимый резерв времени – это часть полного резерва при условии, что предшествующие работы завершаются в поздний срок, а последующие начинаются в ранний срок. Независимый резерв времени принадлежит только данной работе.
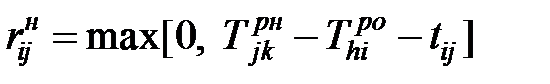 | (1.11) |
Для ручного способа расчёта сетевого графика может использоваться таблица следующего типа (Таблица 1.7):
Таблица 1.7.
| Расчёт аналитических параметров сетевого графика. | ||||||||||
 |  |  |  |  |  |  |  |  |  |  |
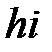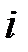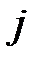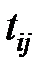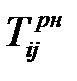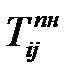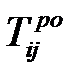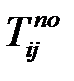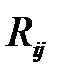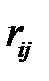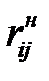В столбец 1 записывают количество предшествующих работ, в столбец 2 – номер начального события, в столбец 3 – номер конечного события, в столбец 4 – время выполнения работы. Остальные столбцы рассчитываются согласно описанным выше правилам. Для модели из примера расчётная таблица будет иметь следующий вид (Таблица 1.8).
Таблица 1.8.
Расчет временных параметров
| | | | | | | | | | | |
| — | ||||||||||
| — | ||||||||||
| — | ||||||||||
| — | — | — | — | — |
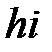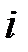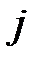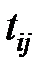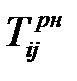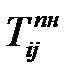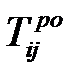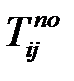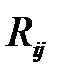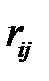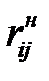Из приведенной таблицы легко увидеть, что путь «0 – 2 – 6 – 8» является критическим, так как резервы времени равны работ нулю (в таблице работы, находящиеся на этом пути, выделены).
Для каждого проекта выбирается своя единица времени в зависимости от масштаба и необходимой точности. Основной целью введения временных параметров является определение продолжительности проекта (длина критического пути), длительности остальных путей, временных резервов путей и отдельных работ с целью дальнейшей оптимизации модели.
Если известна продолжительность каждой работы, можно вычислить длительность всего проекта. Один из базовых и наиболее простых методов анализа – Метод критического пути (МКП) заключается в определении работ (событий), которые должны быть выполнены (наступить) точно в срок, их длительности не могут быть увеличены без увеличения длительности всего проекта. На такие работы обычно направляется больше ресурсов.
Когда все временные параметры вычислены, остаётся только обозначить критический путь на графике. Расчёт критического пути можно проводить, используя особые способы записи на самом графике (четырёхсекторный метод, дробный метод, метод потенциалов). Все методы эквивалентны, так как используют единый аппарат расчёта [11, с. 254].
Вероятностная модель
Рассмотрим теперь случай, когда топология сети детерминирована, а продолжительность работ имеет вероятностную оценку. Методы для расчёта такого типа моделей впервые применялись в рамках методики PERT, о которой уже упоминалось выше.
Пусть продолжительность любой из работ – случайная величина, обладающая такими характеристиками, как средняя продолжительность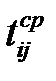 
и дисперсия работы 
.
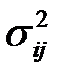Очевидно, что в данном случае на распределение длительности работ накладывается ряд ограничений. Это распределение должно быть неотрицательным, унимодальным, конечным и непрерывным [4]. Для расчёта продолжительности используют так называемые «экспертные» оценки длительности:
- наиболее вероятная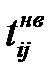 
(в формулах – m);
- пессимистичная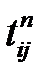 
(в формулах – b);
- оптимистичная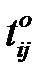 
(в формулах – a).
На основе многочисленных исследований, отмеченных в [3, с. 8], определено, что в качестве закона распределения можно использовать бета-распределение, которое удовлетворяет всем указанным условиям.
Функция плотности бета-распределения определяется на отрезке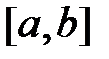 
следующим образом:
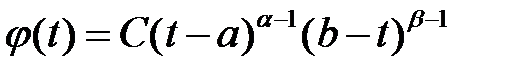 , | (1.12) |
где
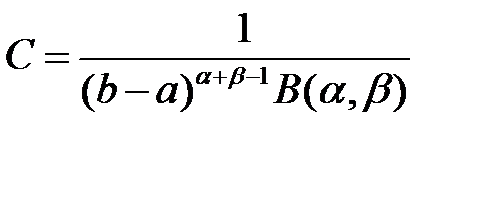 ; | (1.13) |
в свою очередь бета-функция –
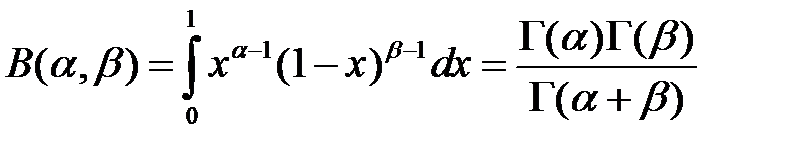 , | (1.14) |
где гамма-функция определяется по формуле
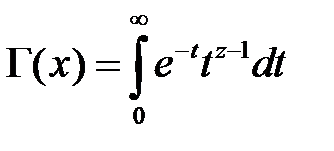 . | (1.15) |
Расчёт коэффициентов бета-функции α и β производится по следующим формулам.
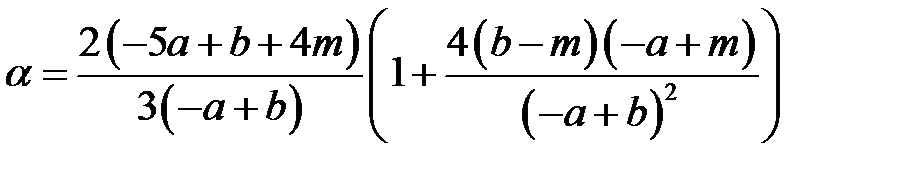 , | (1.16) |
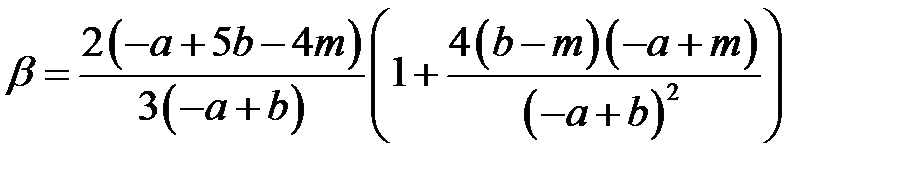 , | (1.17) |
где a – оптимистичная продолжительность работы,
b – пессимистичная продолжительность работы,
m – наиболее вероятная продолжительность работы.
На
Рис. 1.8 изображены график функции плотности вероятности (а) и функции распределения (б) для бета-распределения с параметрами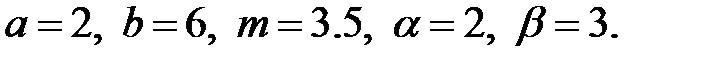 
| - а) плотность; | б) функция распределения. |
Рис. 1.8. Бета-распределение.
Правила вывода формул (1.16) и (1.17) описаны в [22]. Следует отметить, что средняя продолжительность работы является математическим ожиданием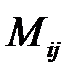 
случайной величины «длительность работы» и вычисляется по формуле
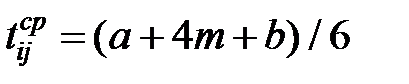 . | (1.18) |
Дисперсия оценки продолжительности работы определяется так:
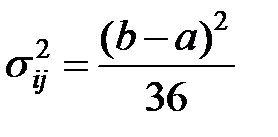 . | (1.19) |
Таким образом,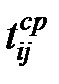 
характеризует наиболее вероятную длительность операции, тогда как 
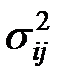определяет величину диапазона возможных длительностей. Чем меньше величина дисперсии, тем меньше неопределённость длительности работы.
Согласно [4], формулы (1.18) и
(1.19) «носят полуэмпирический характер». Голенко-Гинзбургом в качестве альтернативы методам расчёта PERT была предложена модель на основе двух оценок, которая значительно упрощает процесс расчёта и имеет ряд преимуществ перед технологией PERT [4, с. 17], а статистический анализ проекта в этом случае показывает несущественные изменения.
Плотность распределения определена следующим образом:
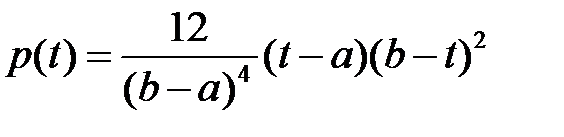 , | (1.20) |
средняя длительность работы:
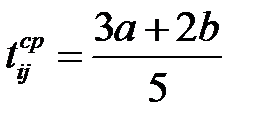 , | (1.21) |
дисперсия:
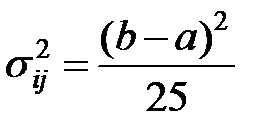 . | (1.22) |
Некоторые авторы предлагают различные альтернативы методу PERT, например метод А. А. Мешкова [5].
Ожидаемую длительность проекта вычисляют как среднюю продолжительность критического пути – это сумма средних длительностей работ, лежащих на этом пути, а отклонение длительности – сумма отклонений работ:
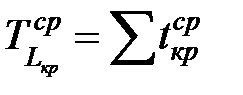 . | (1.23) |
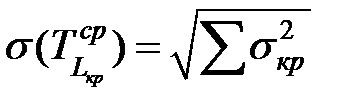 . | (1.24) |
Но величина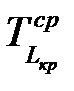 
не всегда удовлетворительна, поэтому дополнительно выбирают директивную продолжительность 
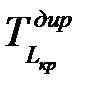[14], и оценивают вероятность завершения работы до предписанного срока 
:
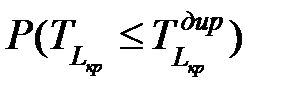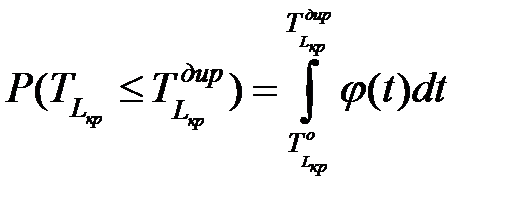 , | (1.25) |
где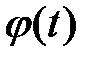 
– функция плотности,
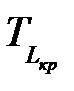– продолжительность критического пути,
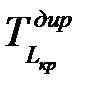– директивная длительность критического пути,
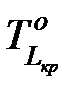– оптимистичная (наименьшая) продолжительность критического пути.
PERT-анализ обладает рядом недостатков, из-за которых вместо него выбирают альтернативные решения. Среди недостатков метода:
- субъективная оценка продолжительности работ;
- выбранная функция распределения для вычисления средней продолжительности работ часто не совпадает с реальным законом распределения;
- для продолжительных проектов оценка с помощью PERT при разработке может кардинально отличаться от оценки, проводимой на одном из этапов реализации (требуются постоянные корректировки);
- неточная оценка критического пути: работы не на критическом пути с большой дисперсией могут стать критическими во время выполнения.
Выводы
Приведенный обзор методов сетевого планирования и управления свидетельствует о широких возможностях их применения для различных классов задач, в том числе и для проектного управления. Выделены три основных типа сетевых моделей: детерминированные сетевые модели (ДСМ), вероятностные сетевые модели (ВСМ), альтернативные сетевые модели (АСМ). Приведены методы расчета временных параметров сетей и методы преобразования (минимизации) сетей.
Обзор программных средств показал, что существуют популярные программы (Microsoft Project, Spider Project, Project Libre, Gantt Pro, Lucid Chart, EDraw Max и др.), автоматизирующие вычисления для МКП, PERT, способные строить диаграммы Гантта и отображать сетевые графики, а также создавать сопутствующую информацию по различным параметрам модели. При этом наблюдается дефицит программного обеспечения для расчётов альтернативных сетей.
Необходимость применения того или иного типа сетевой модели основывается на специфике реализуемого проекта с учётом требований к качеству и ресурсных ограничений. Тем не менее, нет объективных критериев, позволяющих однозначно выбрать тип модели и методы её анализа.
Заключение
В работе в соответствии с целью исследования рассмотрены этапы становления методов сетевого планирования и управления вплоть до современных технологий, мощно поддерживаемых компьютерными средствами расчетов и визуализации.
Проанализированы основные подходы к классификации сетевых моделей по различным признакам и получены сравнительные результаты.
Установлено, что даже на современном этапе использование вероятностных и тем более альтернативных сетевых моделей сопряжено с трудоёмкими рутинными операциями. В Microsoft Project и других подобных системах реализована поддержка задания временных оценок, но их возможности сильно ограничены в случае многокритериальных задач. Что касается программного обеспечения для альтернативных моделей, то можно констатировать его дефицит.
Практические результаты работы связаны с построением примеров использования сетевых моделей в прикладных задачах анализа комплексов работ. Детально приведены этапы анализа по каждой задаче и получены выводы.
Несмотря на недостатки каждого типа моделей, можно сделать следующее утверждение. Для производственных проектов или проектов научного профиля обязательно использовать альтернативные сетевые модели, поскольку эти проекты содержат много проверок (создающих петли и контуры), альтернативы и некоторую степень неопределённости в исходах (эксперимент, контроль качества и др.).
При выполнении практической части произведена оценка числа шагов, расчётов, элементарных операций. Установлено, что ручная оптимизация методом GERT характеризуется большими временными затратами. Поэтому остро стоит вопрос о программных средствах для GERT-анализа.
Список литературы