Производная и ее применение для решения прикладных задач

Ответ:

Физические производные величины:

1) υ(t) = х^/ (t) – скорость

2) a (t)=υ^/ (t) - ускорение

3) J (t) = q^/ (t) - сила тока

4) C(t) = Q^/ (t) - теплоемкость

5) d(l )=m^/ (l ) - линейная плотность

6) K (t) = l ^/ (t) - коэффициент линейного расширения

7) ω (t)= φ^/ (t) - угловая скорость

8) а (t)= ω^/ (t) - угловое ускорение

9) N(t) = A^/ (t) – мощность

Дифференциальное исчисление широко применяется для экономического анализа как математический аппарат. В экономике очень часто требуется найти наилучшее или оптимальное значение показателя: наивысшую производительность труда, максимальную прибыль, максимальный выпуск, минимальные издержки и т. д. Каждый показатель представляет собой функцию от одного или нескольких аргументов. Таким образом, нахождение оптимального значения показателя сводится к нахождению экстремума функции.

Производная в экономических формулах:

П (t) = υ^/ (t) - производительность труда,

где υ (t) - объем продукции

J(x) = y^/ (x) - предельные издержки производства,

где y– издержки производства в зависимости от объема выпускаемой продукции x.

В работе рассмотрены прикладные задачи, способы решения которых можно использовать для решения нестандартных задач по алгебре и началам анализа, при подготовке к государственной итоговой аттестации, внешнему независимому оцениванию. Достаточно большое число задач раскрывают потенциальные возможности анализа бесконечно малых величин.

Понятие производной

Пусть y = f(x) есть непрерывная функция аргумента x, определенная в промежутке (a; b), и пусть х₀ - произвольная точка этого промежутка

Дадим аргументу x приращение ∆x, тогда функция y = f(x) получит приращение ∆y = f(x + ∆x) - f(x). Предел, к которому стремится отношение ∆y / ∆x при ∆x → 0, называется производной от функции f(x).

y'(x)=

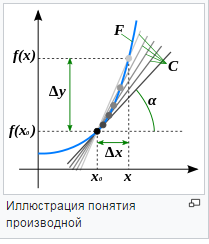
Понятие производной

Пусть y = f(x) есть непрерывная функция аргумента x, определенная в промежутке (a; b), и пусть х₀ - произвольная точка этого промежутка

Дадим аргументу x приращение ∆x, тогда функция y = f(x) получит приращение ∆y = f(x + ∆x) - f(x). Предел, к которому стремится отношение ∆y / ∆x при ∆x → 0, называется производной от функции f(x).

y'(x)=

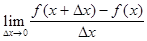
Геометрический смысл производной состоит в том, что она равна угловому коэффициенту касательной. Рассмотрим график функции

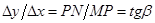(рис.). Видно,что , т.е. это отношение равно угловому

коэффициенту секущей mm. Если 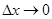, то секущая,поворачиваясь вокруг точки М, в пределе переходит в касательную

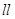, так как касательная является предельным

положением секущей, когда точки пересечения сливаются.

Таким образом,

.

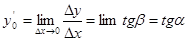
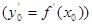Уравнение касательной

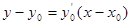, где

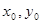- координаты точки касания, а

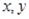- текущие координаты точки касательной прямой.

Физический смысл производнойзаключается в скорости изменения функции.

Пусть s = s (t ) — закон прямолинейного движения. Тогда v (t ₀ ) = s '(t ₀ ) выражает мгновенную скорость движения в момент времени t ₀ . Вторая производная a (t ₀ ) = s ''(t ₀ ) выражает мгновенное ускорение в момент времени t ₀ .Вообще производная функции y = f (x ) в точке x ₀ выражает скорость изменения функции в точке x ₀ , то есть скорость протекания процесса, описанного зависимостью y = f (x ).

Дифференциал

Пусть дана функция

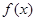и

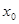- внутренняя точка её области определения. Придадим аргументу приращение

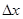и рассмотрим приращение функции

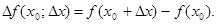
Если это приращение

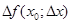можно представить в виде

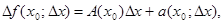где величина

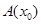не зависит от приращения

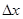, а

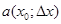- бесконечно малая при

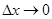величина, имеющая больший порядок малости, чем

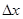, то произведение

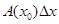называется дифференциалом функции

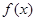в точке

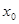и обозначается

.
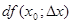