Задача 15. По условию задачи составить дифференциальное уравнение и решить его.

1. Определить кривую, проходящую через точку (3,4), если угловой коэффициент касательной в любой точке кривой равен квадрату ординаты точки касания.

2. Материальная точка с массой 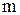движется вдоль оси 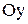, и на нее в каждый момент времени действует сила, пропорциональная отклонению точки от начала координат и направленная к началу координат. Найти закон движения точки, если в момент 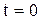она имела ординату 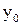и скорость .

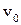3. Корабль замедляет свое движение под действием силы сопротивления воды, которая пропорциональна скорости корабля. Начальная скорость корабля 10 м/с, скорость его через 5 с станет 8 м/с. Когда скорость уменьшится до 1 м/с?

4. Доказать, что кривая, угловой коэффициент касательной в любой точке которой пропорционален абсциссе точки касания, есть парабола.

5. Найти кривую, для которой угловой коэффициент касательной в какой-либо точке в n раз больше углового коэффициента прямой, соединяющей ту же точку с началом координат.

6. Определить путь S, пройденный телом за время t, если его скорость пропорциональная проходимому пути и если тело проходит 100 м в 10 с и 200 м в 15 с.

7. Найти кривую, обладающую тем свойством, что отрезок касательной к кривой, заключенный между осями координат, делится в точке касания пополам.

8. Найти кривую, обладающую тем свойством, что величина перпендикуляра, опущенного из начала координат на касательную, равна абсциссе точки касания.

9. Определить кривую, у которой отношение отрезка, отсекаемого касательной на оси к радиусу-вектору, равно постоянной величине.

10. Найти кривую, для которой длина отрезка, отсекаемого на оси ординат нормалью, проведенной в какой-нибудь точке кривой, равна расстоянию этой точки от начала координат.

11. Точка массы m движется прямолинейно. На нее действует сила, пропорциональна времени (коэффициент пропорциональности 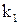). Кроме того, точка испытывает сопротивление среды, пропорциональное скорости (коэффициент пропорциональности 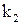). Найти зависимость скорости от времени, считая, что в начальный момент скорости равна нулю.

12. Найти кривые, обладающие тем свойством, что отрезок, который касательная в любой точке кривой отсекает на оси 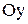, равен квадрату абсциссы точки касания.

13. Найти кривую, в которой отрезок, отсекаемый касательной на оси ординат, равен полусумме координат точки касания.

14. Дана 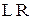– цепь с э.д.с. равной а) 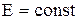, б) 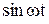. Найдите ток 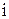в цепи как функцию времени 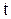, если в начальный момент ток в контуре равен нулю.

15. Найти кривую, для которой произведение абсциссы какой-нибудь точки на величину отрезка, отсекаемого нормалью на оси 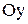, равно удвоенному квадрату расстояния от этой точки до начала координат.

16. Найти время, нужное для того, чтобы упасть на Землю с высоты 400000 км (приблизительно расстояние Луны от центры Земли), если эта высоты исчисляется от центра Земли, и радиус равен приблизительно 6400 км.

17. Материальная точки движется по прямой со скоростью, обратно пропорциональной пройденному пути. В начальный момент движения точка находилась на расстоянии 5 м от начала отсчета пути и имела скорость 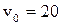м/с. Определить пройденный путь и скорость точки через 10 с после начала движения.

18. Найти закон движения материальной точки массы m по прямой ОА под действием отталкивающей силы, обратно пропорциональной третьей степени расстояния точки 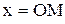от неподвижного центра О.

19. Определить кривую, у которой радиус кривизны равен постоянной величине.

20. Тело массой m падает с некоторой высоты со скоростью v. При падении тело испытывает сопротивление, пропорциональной квадрату скорости. Найти закон движения падающего тела.

21. Материальная точка массы m движется прямолинейно под действием силы F, прямо пропорциональной времени от начала движения и обратно пропорциональной скорости v. Установить зависимость между скоростью v и временем t, если при .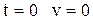

Указание: согласно второму закону Ньютона, .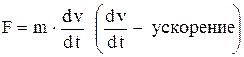

22. Тело движется прямолинейно с ускорением, пропорциональным произведению скорости движения v на время t. Установить зависимость между скоростью и временем, если при .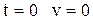

23. Замедляющее действие трения на диск, вращающийся в жидкости, пропорционально угловой скорости 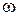. Выразить 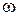как функцию времени, если известно, что за 25 с с начала движения угловая скорость снизилась со 100 об/с до 50 об/с.

24. Найти кривую, проходящую через начало координат, и такую, что площадь треугольника, образованного касательной к кривой в некоторой точке, ординатой этой точки и осью 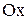, пропорциональна площади криволинейной трапеции, образованной кривой, осью 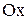и ординатой этой точки.

25. Найти уравнение кривой, проходящей через точку 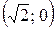, если сумма длин ее касательной и подкасательной равна произведению координат точки касания.

26. Найти уравнение кривой, проходящей через точку (1; 2), если ее подкасательная вдвое больше абсциссы точки касания.

27. Найти уравнения кривых, у которых длина отрезка нормали постоянна и равна а.

28. Найти уравнения кривых, у которых поднормаль имеет постоянную

длину а.

29. Найти уравнение кривой, проходящей через точку 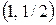, если для любого отрезка 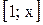площадь криволинейной трапеции, ограниченной соответствующей другой этой кривой, равна отношению абсциссы 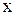концевой точки к ординате.

30. Найти уравнение кривой, проходящей через начало координат, если для любого отрезка 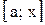площадь криволинейной трапеции, ограниченной соответствующей дугой этой кривой, равна кубу ординаты концевой точки дуги.