Математическое обеспечение САПР (ЛЕКЦИИ)

Математическое обеспечение САПР (ЛЕКЦИИ)

Содержание

• 7.1. Определение, назначение, цель
• 7. 2. Принципы создания САПР конструкции и технологии
• 7.3. Классификация САПР
• 7.4. Структура САПР
• Виды обеспечения САПР
• 7.5. САПР РЭС и их место среди других автоматизированных систем
• Этапы жизненного цикла промышленных изделий
• Контрольные вопросы

Основное назначение лекции - показать сущность процесса проектирования РЭС, основные принципы проектирования. Особенное внимание уделяется системному подходу к проектированию конструкции и технологии производства РЭС.

Содержание

• 8.1. Требования, предъявляемые к техническому обеспечению
• 8.2. Типы сетей
• 8.3. Эталонная модель взаимосвязи открытых систем
• 8.4. Состав технического обеспечения САПР

Основное назначение лекции - показать сущность процесса проектирования РЭС, основные принципы проектирования. Особенное внимание уделяется системному подходу к проектированию конструкции и технологии производства РЭС.

Требования, предъявляемые к техническому обеспечению

Используемые в САПР технические средства должны обеспечивать:

• o выполнение всех необходимых проектных процедур, для которых имеется соответствующее программное обеспечение;
• взаимодействие между проектировщиками и ЭВМ, поддержку интерактивного режима работы;
• взаимодействие между членами коллектива, работающими над общим проектом.

Первое из этих требований выполняется при наличии в САПР вычислительных машин и систем с достаточными производительностью и емкостью памяти.

Второе требование относится к пользовательскому интерфейсуи выполняется за счет включения в САПР удобных средств ввода/вывода данных и, прежде всего, устройств обмена графической информацией.

Третье требование обусловливает объединение аппаратных средств САПР в вычислительную сеть.

В результате общая структура компьютерной сети представляет собой сеть узлов, связанных между собой средой передачи данных (рис. 8.1).

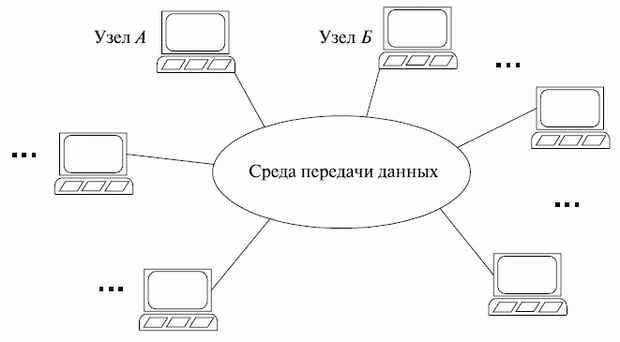
Рис. 8.1. Общая структура компьютерной сети

Узлами (станциями данных) являются рабочие места проектировщиков, часто называемые автоматизированными рабочими местами ( АРМ ), илирабочими станциями (WS - Workstation); ими могут быть также большие ЭВМ ( мейнфреймы ), отдельные периферийные и измерительные устройства.

Именно в АРМ должны существовать средства для интерфейса проектировщика с ЭВМ. Что касается вычислительной мощности, то она может быть распределена между различными узлами вычислительной сети.

Среда передачи данных представлена каналами передачи данных, состоящими из линий связи и коммутационного оборудования.

В каждом узле можно выделить оконечное оборудование данных ( ООД ), выполняющее определенную работу по проектированию, и аппаратуру окончания канала данных ( АКД ), предназначенную для связи ООД со средой передачи данных. Например, в качестве ООД можно рассматривать персональный компьютер, а в качестве АКД - вставляемую в компьютер сетевую плату.

Канал передачи данных - средство двустороннего обмена данными, включающее в себя АКД и линию связи. Линией связи называют часть физической среды, используемую для распространения сигналов в определенном направлении; примерами линий связи могут служить коаксиальный кабель, витая пара проводов, волоконно-оптическая линия связи (ВОЛС).

Близким является понятие канала( канала связи ) ,под которым понимают средство односторонней передачи данных. Примером канала связи может быть полоса частот, выделенная одному передатчику при радиосвязи.

В некоторой линии можно образовать несколько каналов связи, по каждому из которых передается своя информация. При этом говорят, что линия разделяется между несколькими каналами.

Типы сетей

Существуют два метода разделения линии передачи данных: временное мультиплексирование (иначе - разделение по времени,или TDM - Time Division Method),при котором каждому каналу выделяется некоторый квант времени, и частотное разделение (FDM - Frequency Division Method),при котором каналу выделяется некоторая полоса частот.

В САПР небольших проектных организаций, насчитывающих не более единиц-десятков компьютеров, которые размещены на малых расстояниях один от другого (например, в одной или нескольких соседних комнатах), объединяющая компьютеры сеть является локальной. Локальная вычислительная сеть ( ЛВС ), или LAN (Local Area Network),имеет линию связи, к которой подключаются все узлы сети. При этом топология соединений узлов (рис. 8.2) может быть шинная (bus), кольцевая (ring), звездная (star). Протяженность линии и число подключаемых узлов в ЛВС ограничены.

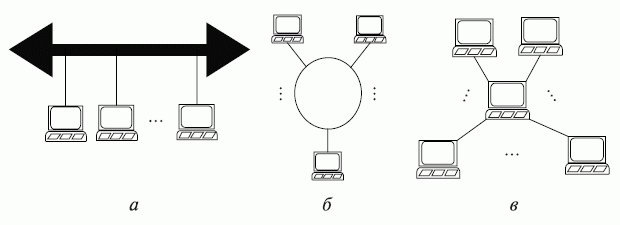
Рис. 8.2. Варианты топологии локальных вычислительных сетей: а - шинная; б - кольцевая; в - звездная

В более крупных по масштабам проектных организациях в сеть включены десятки-сотни и более компьютеров, относящихся к разным проектным и управленческим подразделениям и размещенных в помещениях одного или нескольких зданий. Такую сеть называют корпоративной .В ее структуре можно выделить ряд ЛВС, называемых подсетями,и средства связи ЛВС между собой. В эти средства входят коммутационные серверы (блоки взаимодействия подсетей). Если коммутационные серверы объединены отделенными от ЛВС подразделений каналами передачи данных, то они образуют новую подсеть, называемую опорной (или транспортной), а вся сеть оказывается иерархической структуры.

Если здания проектной организации удалены друг от друга на значительные расстояния (вплоть до их расположения в разных городах), то корпоративная сеть по своим масштабам становится территориальной сетью (WAN- Wide Area Network).В территориальной сети различают магистральные каналы передачи данных ( магистральную сеть ), имеющие значительную протяженность, и каналы передачи данных, связывающие ЛВС (или совокупность ЛВС отдельного здания или кампуса) с магистральной сетью и называемые абонентской линией или соединением "последней мили".

Обычно создание выделенной магистральной сети, т. е. сети, обслуживающей единственную организацию, обходится для этой организации слишком дорого. Поэтому чаще прибегают к услугам провайдера,т. е . фирмы, предоставляющей телекоммуникационные услуги многим пользователям. В этом случае внутри корпоративной сети связь на значительных расстояниях осуществляется через магистральную сеть общего пользования. В качестве такой сети можно использовать, например, городскую или междугородную телефонную сеть или территориальные сети передачи данных. Наиболее распространенной формой доступа к этим сетям в настоящее время является обращение к глобальной вычислительной с ети Internet.

Для многих корпоративных сетей возможность выхода в Internet является желательной не только для обеспечения взаимосвязи удаленных сотрудников собственной организации, но и для получения других информационных услуг. Развитие виртуальных предприятий, работающих на основе CALS-технологий, с необходимостью подразумевает информационные обмены через территориальные сети, как правило, через Internet. Нужно, однако, отметить, что использование сетей общего пользования существенно усложняет задачу обеспечения информационной безопасности.

Структура ТО САПР для крупной организации представлена на рис. 8.3.

Здесь показана типичная структура крупных корпоративных сетей САПР, называемая архитектурой клиент-сервер.В сетях "клиент-сервер" выделяется один или несколько узлов, называемых серверами,которые выполняют в сети управляющие или общие для многих пользователей проектные функции, а остальные узлы (рабочие места) являются терминальными - их называют клиентами,в них работают пользователи.

В общем случае сервером называют совокупность программных средств, ориентированных на выполнение определенных функций.Но если эти средства сосредоточены на конкретном узле вычислительной сети, то тогда понятие "сервер" относится именно к узлу сети.

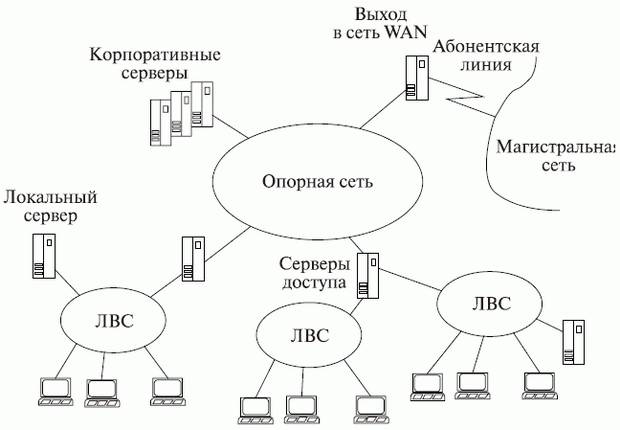
Рис. 8.3. Структура корпоративной сети САПР

Сети "клиент-сервер" различают по характеру распределения функций между серверами - другими словами, их классифицируют по типам серверов. Различают файл-серверы для хранения файлов, разделяемых многими пользователями, серверы баз данных АС, серверы приложений для решения конкретных прикладных задач, коммутационные серверы (называемые также блоками взаимодействия сетей или серверами доступа) для взаимосвязи сетей и подсетей, специализированные серверы для выполнения определенных телекоммуникационных услуг, например серверы электронной почты. В случае специализации серверов по определенным приложениям сеть называют сетью распределенных вычислений.Если сервер приложений обслуживает пользователей одной ЛВС, то такой сервер называют локальным. Но поскольку в САПР имеются приложения и базы данных, разделяемые пользователями разных подразделений и, следовательно, кли ентами разных ЛВС, соответствующие серверы относят к группе корпоративных, подключаемых обычно к опорной сети.

Наряду с архитектурой "клиент-сервер" применяют одноранговые сети, в которых любой узел в зависимости от решаемой задачи может выполнять функции как сервера, так и клиента. Организация взаимодействия в таких сетях при числе узлов более нескольких десятков становится довольно сложной, поэтому одноранговые сети нашли преимущественное распространение в небольших по масштабам САПР.

В соответствии со способами коммутации различают сети с коммутацией каналов и коммутацией пакетов.В первом случае при обмене данными между узлами А и В сети создается физическое соединение между А и В, которое во время сеанса связи используется только этими абонентами. Примером сети с коммутацией каналов может служить телефонная сеть. Здесь передача информации происходит быстро, но каналы связи используются неэффективно, так как при обмене данными возможны длительные паузы и канал "простаивает". При коммутации пакетов физического соединения, которое в каждый момент сеанса связи соединяло бы абонентов А и В, не создается. Сообщения разделяются на порции, называемые пакетами,которые передаются в разветвленной сети от А к В или обратно через промежуточные узлы с возможной буферизацией (временным запоминанием) в них. Таким образом, любая ли ния может разделяться многими сообщениями, попеременно пропуская при этом пакеты разных сообщений с максимальным заполнением упомянутых пауз.

9. Лекция: Технические средства САПР и их развитие (окончание)

Рассматриваются состав, классификация, потоки команд, потоки данных, составляющих основу технического обеспечения современных САПР.

Содержание

• 9.1. Высокопроизводительные технические средства САПР и их комплексирование
• 9.2. Режимы работы технических средств САПР
• 9.3. Разработка технического обеспечения САПР

Цель лекции заключается в создании полной характеристики технического обеспечения САПР.

Содержание

• 10.1. Назначение и состав методического обеспечения САПР
• 10.2. Математическое обеспечение САПР
• 10.3. Лингвистическое обеспечение САПР
• 10.4. Программное обеспечение САПР

Изучение одного из важнейших видов обеспечения САПР - методического обеспечения и его составных частей: математического и лингвистического видов обеспечения.

Содержание

• 11.1. Назначение, сущность и составные части информационного обеспечения (ИО) САПР
• 11.2. Уровни представления данных
• 11.3. Проектирование базы данных

Основное назначение лекции - представление информационного обеспечения САПР как составной части современных информационных технологий. Именно с этой позиции рассматриваются назначение, сущность и состав информационного обеспечения.

Содержание

• 12.1. Иерархическая структура проектных спецификаций и иерархические уровни проектирования
• 12.2. Требования к математическим моделям
• 12.3. Классификация ММ

Показать необходимость блочно-иерархического подхода к проектированию РЭС и необходимость включения в качестве своей основы иерархию математических моделей.

Требования к математическим моделям

При построении математических моделей используют различные математические средства описания объекта - теорию множеств, теорию графов, теорию вероятностей, математическую логику, математическое программирование, дифференциальные или интегральные уравнения и т. д.

Выполнение проектных операций и процедур в САПР основано на оперировании ММ. С их помощью прогнозируются характеристики и оцениваются возможности предложенных вариантов схем и конструкций, проверяется их соответствие предъявляемым требованиям, проводится оптимизация параметров, разрабатывается техническая документация.

В САПР для каждого иерархического уровня сформулированы основные положения математического моделирования - выбран и развит соответствующий математический аппарат, получены типовые ММ элементов проектируемых объектов, формализованы методы получения и анализа математических моделей систем. Сложность задач проектирования и противоречивость требований высокой точности, полноты и малой трудоемкости анализа обусловливают целесообразность компромиссного удовлетворения этих требований с помощью соответствующего выбора моделей. Это обстоятельство приводит к расширению множества используемых моделей и развитию алгоритмов адаптивного моделирования.

Основными требованиями, предъявляемыми к математическим моделям, являются требования адекватности, универсальности и экономичности.

Модель считается адекватной, если отражает заданные свойства объекта с приемлемой точностью. Точность определяется как степень совпадения значений выходных параметров модели и объекта. Пусть 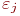- относительная погрешность модели по 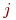-му выходному параметру

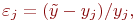(12.1)

где 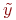- -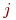й выходной параметр, рассчитанный с помощью модели;

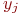- тот же выходной параметр, существующий в моделируемом объекте.

Погрешность модели 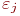по совокупности учитываемых выходных параметров оценивается одной из норм вектора .

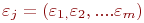Точность модели различна в разных условиях функционирования объекта. Эти условия характеризуются внешними параметрами. Если задаться предельной допустимой погрешностью \varepsilon _{пред}, то можно в пространстве внешних параметров выделить область, в которой выполняется условие

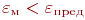(12.2)

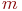Эту область называют областью адекватности (ОА) модели. Возможно введение индивидуальных предельных значений для каждого выходного параметра и определение ОА как области, в которой одновременно выполняются все условий вида .

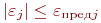Определение областей адекватности для конкретных моделей - сложная процедура, требующая больших вычислительных затрат. Эти затраты и трудности представления ОА быстро растут с увеличением размерности пространства внешних параметров. Определение ОА - более трудная задача, чем, например, задача параметрической оптимизации. Для моделей унифицированных элементов расчет областей адекватности становится оправданным в связи с однократностью определения ОА и многократностью их использования при проектировании различных систем. Знание ОА позволяет правильно выбирать модели элементов из числа имеющихся и тем самым повышать достоверность результатов машинных расчетов.

В библиотеку моделей элементов, наряду с алгоритмом, реализующим модель, и номинальными значениями параметров, должны включаться граничные значения внешних параметров 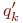и 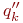, задающие область адекватности.

При определении ОА необходимо выбрать совокупность внешних параметров и совокупность выходных параметров 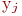, отражающих учитываемые в модели свойства. Типичными внешними параметрами при этом являются параметры нагрузки и внешних воздействий (электрических, механических, тепловых, радиационных и т. п.). Увеличение числа учитываемых внешних факторов расширяет применимость модели, но существенно удорожает работу по определению ОА. Выбор совокупности выходных параметров также неоднозначен, однако для большинства объектов число и перечень учитываемых свойств и соответствующих им выходных параметров сравнительно невелики, достаточно стабильны и составляют типовой набор выходных параметров. Например, для макромоделей логических элементов БИС такими выходными параметрами являются уровни выходного напряжения в состояниях логических "0" и "1", запасы помехоустойчивости, задержка распространения сигнала, рассеиваемая мощность.

Если адекватность характеризуется положением и размерами ОА, то универсальность модели определяется числом и составом учитываемых в модели внешних и выходных параметров.

Экономичность модели характеризуется затратами вычислительных ресурсов для ее реализации, а именно затратами машинного времени 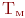и памяти 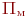. Общие затраты 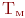и 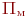на выполнение в САПР какой-либо проектной процедуры зависят как от особенностей выбранных моделей, так и от методов решения.

В большинстве случаев при реализации численного метода происходят многократные обращения к модели элемента, входящего в состав моделируемого объекта. Тогда удобно экономичность модели элемента характеризовать затратами машинного времени при обращении к модели, а число обращений к модели должно учитываться при оценке экономичности метода решения.

Экономичность модели по затратам памяти оценивается объемом оперативной памяти, необходимой для реализации модели.

Требования широких областей адекватности, высокой степени универсальности, с одной стороны, и высокой экономичности - с другой, являются противоречивыми. Наилучшее компромиссное удовлетворение этих требований оказывается неодинаковым в различных применениях. Это обстоятельство обусловливает использование в САПР многих моделей для объектов одного и того же типа - различного рода макромоделей, многоуровневых, смешанных моделей и т. п.

13. Лекция: Математические модели (ММ) на различных иерархических уровнях

Приводится иерархия математических моделей как основа блочно-иерархического подхода к проектированию радиоэлектронных средств.

Содержание

• 13.1. Иерархия математических моделей в САПР
• 13.2. Микро-, макро- и метауровни
• Математические модели на микроуровне
• Математические модели на макроуровне
• Математические модели на метауровне
• Математические модели с использованием целочисленного программирования
• Математические модели с использованием систем массового обслуживания
• Математические модели с использованием сетей Петри
• 13.3. Структурные модели

Назначение лекции - показать основу, базу современного подхода к проектированию РЭС, дать более глубокие сведения о математических моделях, используемых при проектировании РЭС.

Микро-, макро- и метауровни

В зависимости от сложности объекта при его проектировании используют большее или меньшее число уровней абстракции. Объединение уровней, родственных по характеру используемого математического аппарата, приводит к образованию в иерархии функциональных моделей для большинства проектируемых сложных объектов трех укрупненных уровней: микро-, макро- и метауровней.

На микроуровне используют математические модели, описывающие физическое состояние и процессы в сплошных средах. Для моделирования применяют аппарат уравнений математической физики. Примерами таких уравнений служат дифференциальные уравнения в частных производных - уравнения электродинамики, теплопроводности, упругости, газовой динамики. Эти уравнения описывают поля электрического потенциала и температуры в полупроводниковых кристаллах интегральных схем. К типичным фазовым переменным на микроуровне относятся электрические потенциалы, давление, температура, концентрации частиц, плотности токов. Независимыми переменными являются время и пространственные координаты. В качестве операторов 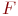и 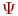в уравнениях (13.2) фигурируют дифференциальные и интегральные операторы. Уравнения (13.2), дополненные краевыми условиями, составляют ММ объектов на микроуровне. Анализ таких моделей сводится к решению краевых задач математической физики.

На макроуровне производится дискретизация пространств с выделением в качестве элементов отдельных деталей, дискретных электрорадиоэлементов, участков полупроводниковых кристаллов. При этом из числа независимых переменных исключают пространственные координаты. Функциональные модели на макроуровне представляют собой системы алгебраических или обыкновенных дифференциальных уравнений. Для их получения и решения используют соответствующие численные методы. В качестве фазовых переменных фигурируют электрические напряжения, токи, силы, скорости, температуры, расходы и т. д. Они характеризуют проявления внешних свойств элементов при их взаимодействии между собой и внешней средой в электронных схемах или механических конструкциях.

На метауровне с помощью дальнейшего абстрагирования от характера физических процессов удается получить приемлемое по сложности описание информационных процессов, протекающих в проектируемых объектах. На метауровне для моделирования аналоговой РЭС широко применяют аппарат анализа систем автоматического управления, а для моделирования цифровой РЭС - математическую логику, теорию конечных автоматов, теорию массового обслуживания. Математические модели на метауровне - системы обыкновенных дифференциальных уравнений, системы логических уравнений, имитационные модели систем массового обслуживания.

Содержание

• 17.1. Основные понятия
• 17. 2. Части графа
• 17. 3. Способы задания графов
• Матрица смежности
• Матрица весовых соотношений
• Матрица инцидентности
• Контрольные вопросы

Изложить основные понятия теории графов, знание которых является обязательным при современном конструкторском проектировании РЭС.

Основные понятия

Теорию графов применяют для решения таких задач, как анализ электронных схем, разбиение и размещение электронных элементов, проектирование проводного и печатного монтажа, сетевое планирование и многих других. Это объясняется тем, что использование графов сокращает объём вычислений по сравнению с другими методами и, сохраняя наглядность описания объектов (конструкций), позволяет строить компактные и удобные для реализации на ЭВМ алгоритмы преобразований и оптимизации.

Понятие графа 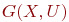опирается на понятие множества.

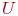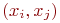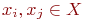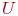Под абстрактным графом или просто графом G(X,U) понимают совокупность непустого множества и изолированного от него подмножества (возможно, пустого), представляющего собой множество всех упорядоченных пар , где . Элементы множеств и называют, соответственно, вершинами и дугами графа. Следовательно, граф - это множество всех вершин , связи между которыми определены множеством рёбер .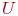

Геометрически граф можно представить в виде множества точек 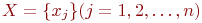в 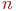-мерном евклидовом пространстве 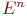и множества простых, направленных самонепересекающихся кривых

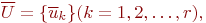
соединяющих 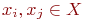, которые находятся в некотором отношении друг к другу.

То, что элемент 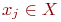находится в отношении 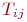к элементу 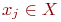, отображается на графе соединением элементов и 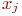линией со стрелкой в направлении от к 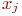. Такие соединения вершин графа с указанием направления называют ориентированными рёбрами или дугами и записывают так:

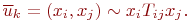
Граф, в котором все вершины соединены дугами, называют ориентированным, направленным или несимметрическим графом.

Аналитически любой ориентированный граф описывается системой алгебраических уравнений, связывающих параметры 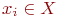, и наоборот, любая система алгебраических уравнений может быть представлена в виде направленного графа.

Пример. Рассмотрим граф, показанный на рис. 17.1.

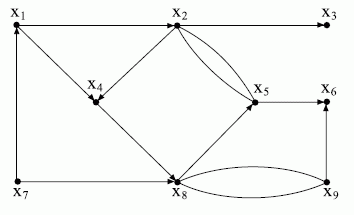
Рис. 17.1. Ориентированный граф

Этот граф определяет следующую систему уравнений:

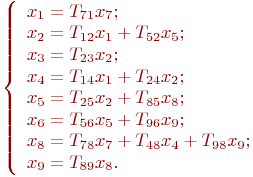
Граф, в котором для любых двух вершин 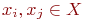справедливо выражение 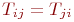, называют неориентированным, ненаправленным или симметрическим графом.

В таком графе вершины и 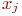соединены ненаправленной кривой, называемой неориентированным ребром или просто ребром графа (рис. 17.2).

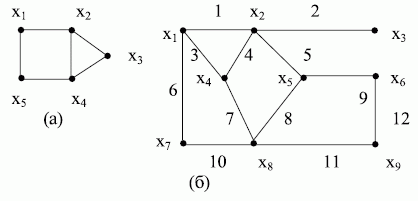
Рис. 17.2. Неориентированные графы

В дальнейшем рассматриваются в основном неориентированные графы, т.к. при решении большинства задач конструкторского проектирования существенным является лишь наличие или отсутствие связей между отдельными элементами конструкции.

При анализе электронных схем, наоборот, пользуются только направленными графами.

На рис. 17.2 неориентированные рёбра обозначены цифрами 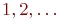.и т.д.

Две вершины 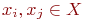считаются смежными, если они определяют ребро ( дугу ) и, соответственно, два различных ребра ( дуги ) смежны, если они имеют общую вершину.

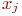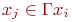Иными словами, вершина смежна , если , где 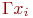- отображение на множестве .

В связи с тем, что отображение 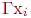представляет собой совокупность всех вершин графа 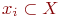, смежных 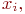получаем ещё один способ задания графа:

Граф задан, если задано непустое множество 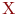и отображение 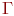множества 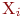в 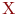. Обозначим его 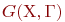. При геометрической реализации такого графа каждую вершину 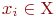соединяют со всеми вершинами .

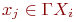Например, для графа 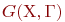(рис. 17.2,б) можно записать:

(.\)

Для графа

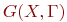
(рис. 17.2, а) запись будет следующей:

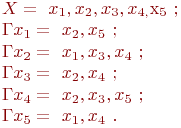
Вершина инцидента ребру ( дуге ) 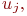если она является началом или концом ребра ( дуги ). Аналогично утверждение, что ребро ( дуга ) 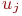инцидентно вершине , если оно входит или выходит из этой вершины.

Число рёбер ( дуг ), инцидентных некоторой вершине , называют локальной степенью вершины и обозначают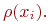

Для графа (рис. 17.2, б) можно записать:

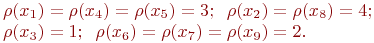
Учитывая, что каждое ребро неориентированного графа инцидентно двум вершинам, получим выражение, связывающее число рёбер графа со степенями вершин

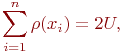(U()

где 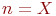- число вершин графа;

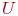- число рёбер графа.

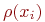Из этого выражения следует, что число вершин с нечётной степенью в графе чётное, так как при опускании всех вершин с чётными степенями сумма слева остаётся чётной.

Вершину, неинцидентную никакому ребру ( дуге ), называют изолированной.

Граф, состоящий только из изолированных вершин ( 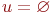), называют нуль - графом и обозначают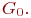

При использовании графов для анализа радиоэлектронных устройств в отдельных случаях целесообразно введение связи вершины самой с собой, т.е.

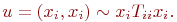
Такую связь называют петлёй.

Если граф 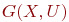имеет петлю при вершине 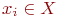, то .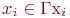

Отсюда следует, что необходимым и достаточным условием отсутствия петель в графе является

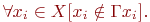
При геометрической реализации графа петля представляется замкнутой дугой, начинающейся и оканчивающейся в одной и той же вершине

и не проходящей через другие вершины графа. Поскольку концевые точки петли совпадают, то петлю считают неориентированной.

Граф называют конечным,если число его рёбер конечно и бесконечным, если число его рёбер бесконечно.

Граф называют однородным степени t, если степени всех его вершин равны t , т.е.

Лекция: Характеристические числа графов и их применение в конструкторском проектировании РЭС

Рассматриваются некоторые характеристические числа графа, позволяющие в ряде случаев упростить решение задач исследования топологических свойств графа.

Содержание

• 18. 1. Цикломатическое число
• 18. 2. Хроматическое число
• 18.3. Плоские графы
• Критерии планарности графов
• Разбиение графа на плоские суграфы
• 18.4. Представление конструкции РЭС с помощью графов
• Контрольные вопросы

Изложить основные понятия теории графов, знание которых является обязательным при современном конструкторском проектировании РЭС.

Рассмотрим некоторые характеристические числа графа, позволяющие в ряде случаев упростить решение задач исследования топологических свойств графа. К таким числам, не зависящим от изоморфных преобразований, относятся: цикломатическое 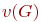и хроматическое 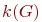числа, числа внутренней 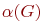и внешней 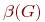устойчивости графа.

Цикломатическое число

При рассмотрении произвольного неориентированного графа 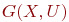без петель с 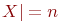и 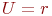, состоящего из " 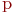" компонент связности, величину

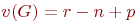(18.1)

называют цикломатическим числом графа.

Иногда вводят понятие ранга графа

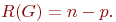(18.2)

В этом случае цикломатическое число

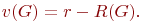(18.3)

Цикломатическое число графа указывает то наименьшее число рёбер, которое нужно удалить из данного графа, чтобы получить дерево (для связного графа) или лес (для несвязного графа), т.е. добиться отсутствия у графа циклов.

Цикломатическое число всегда неотрицательно.

Основное свойство цикломатического числа формулируется в виде теоремы:

Цикломатическое число мультиграфа равно максимальному числу независимых циклов.

Знание цикломатического числа оказывается полезным при анализе топологии электронных схем, а также для решения целого класса задач конструкторского проектирования РЭС.

Пример. Если рассматривать конструкцию печатной платы, то схему электрических соединений можно интерпретировать графом 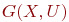, где - множество областей контактных площадок, внутри которых проведение проводников запрещено, a 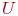- множество трасс.

При этом всё коммутационное пространство разбивается проведёнными соединениями на отдельные, локально замкнутые области

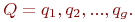(18.4)

Любые две вершины 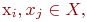находящиеся в различных областях 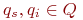, не могут быть соединены ребром 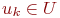без пересечения рёбер (соединений), ограничивающих област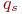и и .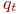

В связи с этим возникает необходимость контроля непопадания смежных вершин в различные изолированные области.

Цикломатическое число 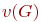позволяет определить ч