Метод кортежей для представления градуированных сетей

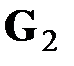Легко видеть, что предложенная выше группа геометрических показателей, вообще говоря, не определяет сетевую структуру однозначно (в отличие от матрицы смежности) – легко построить примеры неизоморфных сетей и , обладающих одинаковыми значениями перечисленных выше коэффициентов. Тем не менее, в работе [12] высказывалось предположение, что предложенная группа геометрических коэффициентов, будучи модифицированной (измененной или расширенной некоторым дополнительным списком геометрических характеристик сети), в совокупности может дать вполне определенное представление о строении организационной сети и даже определять эту организационную сеть однозначно с точностью до изоморфизма. Далее мы покажем, что это действительно так – мы модифицируем введенные геометрические характеристики и с их помощью полностью решим задачу определяемости градуированных сетей набором геометрических характеристик.

Решение поставленной задачи об определяемости сетей оказывается возможным благодаря методу кортежей, впервые введенному в [14]. Метод кортежей, наряду с матрицами смежности, даёт еще один, более простой способ задания и описания сетей [15]. С математической точки зрения, дальнейшие построения и результаты настоящего и следующего разделов означают полноту и категоричность [16] представленного набора геометрических характеристик.

Пусть дана градуированная сеть 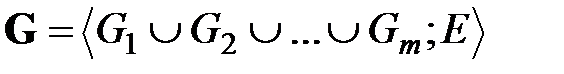. Определим для каждого узла , лежащего на уровне , две характеристики:

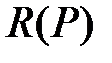– количество ребер (степень вершины, число организационных связей), идущих из узла 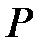в узлы того же ранга, т.е. в узлы того же уровня 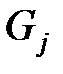, на котором лежит узел ;

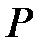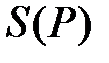– количество ребер (степень вершины, число организационных связей), идущих из узла 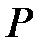в узлы следующего ранга, т.е. в узлы уровня 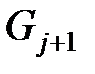, лежащего непосредственно под уровнем узла .

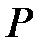По определению градуированной сети, ребра из узла 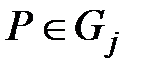в узлы уровня 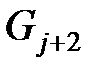идти не могут, поэтому общее число ребер, исходящих из узла 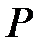в узлы равного или меньшего рангов точности равно .

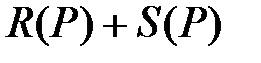Занумеруем произвольным образом натуральными числами узлы каждого уровня 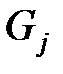, т.е. сопоставим каждому узлу 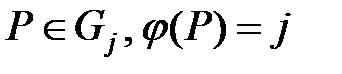некоторое натуральное число 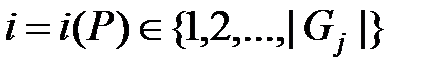– номер этого узла на уровне 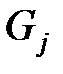, здесь 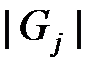– количество узлов сети ранга , т.е. число элементов на уровне 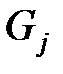. Подразумеваем, естественно, что нумерация 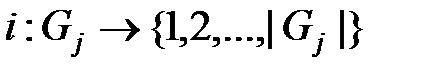является биективным [5,6] отображением, в частности, номера разных узлов 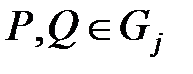не могут совпадать: 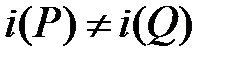. Легко видеть, что различных нумераций данного уровня 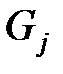всего существует 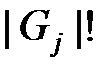штук.

После того, как узлы каждого уровня сети занумерованы, сопоставим каждому узлу 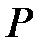сети следующий кортеж натуральных чисел:

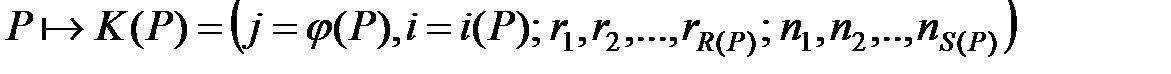. (1)

В кортеже первые два числа суть ранг 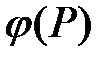узла 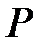и номер 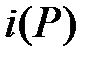узла 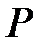на его уровне 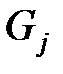в зафиксированной нумерации. Назовем первые два числа 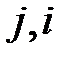кортежа его префиксной частью.

Числа 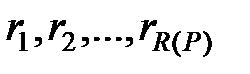суть номера узлов на уровне 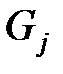, инцидентных узлу 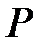(связанных с ним организационной связью), то есть номера узлов, смежных с узлом 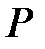на уровне 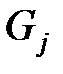(все эти узлы имеют ранг, равный рангу узла 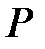). Договоримся, что если узел 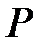не связан с узлами своего уровня 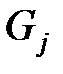, то в кортеже на месте группы чисел 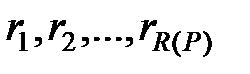стоит число 0. Числа 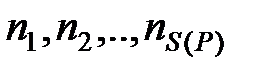суть номера узлов на уровне 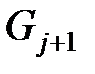, инцидентных узлу 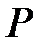, т.е. номера узлов, лежащих на следующем (более низком) уровне 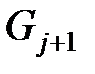и связанных с узлом 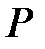(все такие узлы имеют ранг, в точности равный 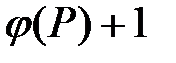). Договоримся, что если узел 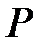не связан с узлами следующего уровня 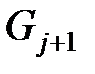, то в кортеже на месте группы чисел 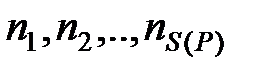стоит число 0. Будем называть числа 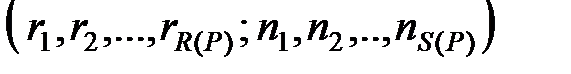– суффиксной частью кортежа .

В результате сопоставления всем узлам сети соответствующих кортежей, получим набор кортежей вида (1) для всех узлов сети . Каждый кортеж является геометрической характеристикой узла сети – в кортеже содержится информация о ранге узла и его организационных связях.

По набору кортежей построим таблицу кортежей , организованную следующим образом – в -й строке таблицы кортежей расположены все кортежи узлов уровня 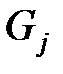в порядке возрастания номеров этих узлов, т.е. первые два числа каждого кортежа являются, соответственно, номером строки и номером столбца ячейки таблицы, в котором находится данный кортеж . (Отметим, что после организации кортежей в таблицу, в целях экономии памяти, первые два числа из каждого кортежа (префиксную часть) можно удалить, поскольку префикс однозначно восстанавливается по расположению кортежа в таблице ).

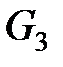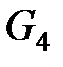уровни

Рис. 2.7. Пример градуированной сети и соответствующей таблицы кортежей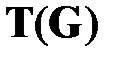

Таблица кортежей 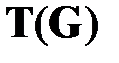(1,1; 0; 1,2)       (2,1; 0; 1,2) (2,2; 0; 3,4)     (3,1; 2; 0) (3,2; 1; 0) (3,3; 0; 1,2) (3,4; 0; 2,3) (4,1; 0; 0) (4,2; 0; 0) (4,3; 0; 0)

Сеть

Пример градуированной сети и соответствующей таблицы кортежей приведен на рисунке 2.7.