Задачи прочности и устойчивости для мультиоператорных сетей

Организационные сети в практической деятельности изучаются с различных точек зрения – оптимизации потоков в сетях, задачи коммивояжера, задачи дискретной оптимизации, расчеты и прогнозирование эффективности процессов производства, управления, распределения ресурсов, инвестирования и т.д.

В условиях нормального функционирования экономики, а в еще большей степени – в условиях ее кризисного состояния, значительный интерес вызывает круг вопросов, связанный с прочностью и устойчивостью организационных структур. На практике постоянно происходят процессы преобразования сетей; одни сети распадаются, другие трансформируются, третьи перестают выполнять свои функции, начинают давать сбои и т.п.

Что происходит, и что может происходить с мультиоператорными сетями – важная и актуальная исследовательская задача (особенно в условиях кризиса, обостряющего и усиливающего воздействия на сетевые организационные структуры). Класс теоретических и практических задач прочности и устойчивости сетей (особенно в своей общей постановке – для многоосновных мультиоператорных сетей) является новой проблематикой в развитии теории организационных сетей, новым направлением исследований.

С нашей точки зрения, в этой проблематике, формально, можно выделить два широких класса задач.

Первый класс задач связан с геометрической (топологической) прочностью мультиоператорной сети. Задачи этого класса апеллируют к различным геометрическим и топологическим характеристикам рассматриваемых сетей. Очевидно, что, например, внешнее воздействие на сеть (действие сигнатурного оператора 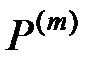), заключающееся в удалении или трансформации ребер или узлов сети, может привести к распаду (или разрыву) всей сети. Сеть перестанет, например, быть связной, распадется на отдельные фрагменты (несвязные компоненты) или резко уменьшится коэффициент связности между различными секторами сети.

На практике это может означать, что в результате какого-то внешнего воздействия, влекущего удаление ребер или узлов действующей сетевой структуры, ее реальная организационно-правовая или организационно-экономическая форма утратит свои функции, сеть разорвется, отдельные предприятия выйдут из общего организационного и экономического поля, экономические связи разрушатся. Практические последствия разрывов сети вследствие внешних воздействий могут быть крайне негативными.

Совершенно очевидно, что изучение вопросов прочности (живучести) сетей напрямую связано с организационной устойчивостью тех или иных организационных структур, с их жизнеспособностью, с экономической безопасностью регионов и подразделений, с энергетической и транспортной безопасностью регионов и т.д.

С формальной математической точки зрения, очерченный круг вопросов в проблематике прочности и устойчивости мультиоператорных сетей может быть представлен следующим образом. Пусть дана мультиоператорная сеть 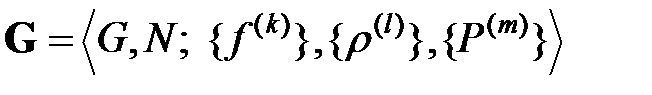. Удаление (закрытие) каких множеств 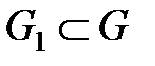и 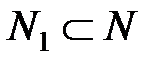(т.е. узлов и ребер), и обнуление (закрытие) каких потоков 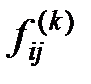между узлами сети приведет к распаду сети 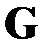на несвязные фрагменты? Ослабленный вариант постановки этой задачи – какое воздействие на сеть 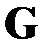некоторого «внешнего» оператора 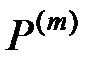повлечет критическое сокращение сетевых показателей эффективности работы получившейся сети ?

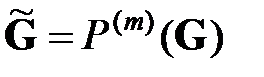Второй класс задач, относящихся к прочности и устойчивости сетей, связан с реальными часто происходящими ситуациями, когда разрыва и распада сети не происходит, но рассматриваемая сеть по тем или иным параметрам, показателям и оценкам, перестает выполнять свои функции. Это круг внутрисетевых вопросов, охватывающий устойчивость производственных процессов и стабильность внутриструктурных связей.

В этом круге вопросов, как правило, имеется некоторый оценочный функционал 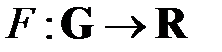, который по параметрам работы сети определяет некоторую числовую оценку 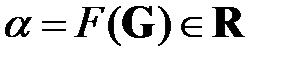качества и приемлемости процессов, протекающих в сети. Как только эта оценка, в силу каких-либо негативных случайных воздействий операторов 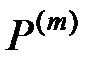на сеть, стала неудовлетворительной: 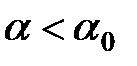, где 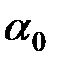– некоторое критическое значение оценочного параметра, будем говорить, что в сети возникла критическая ситуация по параметру оценки .

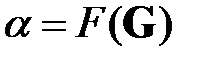Примером критической ситуации в сетевой структуре может служить следующая весьма часто возникающая производственная ситуация. Пусть, например, на узел-предприятие 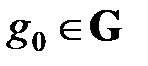осуществляются поставки сырья с разных узлов 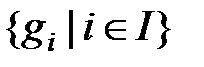рассматриваемой сети (рис. 2.3).

Орбита 1

Орбита 2

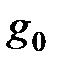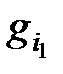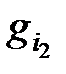Рис.2.3. Фрагмент мультиоператорной сети G. Узел 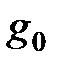со своими поставщиками-смежниками

Как только суммарный объем поставок 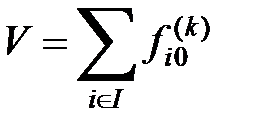некоторого k-го типа сырья в сторону узла 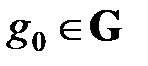со стороны узлов-поставщиков (узлов орбиты №2) уменьшился ниже допустимого уровня 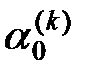(критического для производства), в сети возникает критическая ситуация, описываемая неравенством .

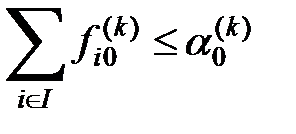Критическая ситуация не означает напрямую, что рассматриваемая сеть распалась или произошел разрыв на несвязные компоненты. Однако возникновение критических ситуаций, как правило, требует стабилизирующих воздействий: оперативного организационного нормирования и регламентирования, управленческих и производственных решений, принятия законов, финансовых займов, государственной поддержки и т.п.

Следует отметить, что при анализе и решении задач второго типа, наряду с традиционными дискретными методами анализа сетей, необходимо применять различные методы классической непрерывной математики, теории рисков, аппарата теории вероятностей и математической статистики. Это обстоятельство в значительной степени мотивируется тем, что операторы воздействия 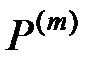на сеть в общем случае являются стохастическими и отражают случайный характер внешних воздействий на рассматриваемую сеть (директивных воздействий, сбоев, невыполнений контрактов, различных форс-мажорных ситуаций), приводящих к возникновению критических ситуаций в сетях по одному или нескольким параметрам оценки 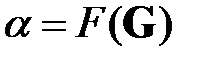.