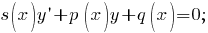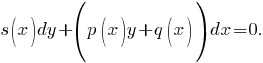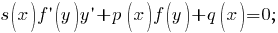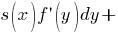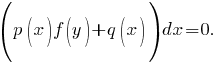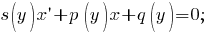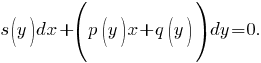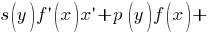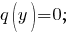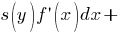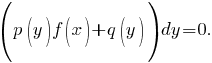Экстремум функции двух переменных
Говорят, что функция 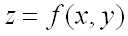 имеет максимум в точке
имеет максимум в точке 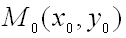 , т.е. при
, т.е. при 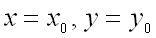 , если
, если 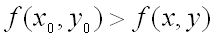 для всех точек
для всех точек 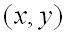 , достаточно близких к точке
, достаточно близких к точке 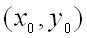 и отличных от неё.
и отличных от неё.
Говорят, что функция 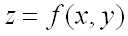 имеет минимум в точке
имеет минимум в точке 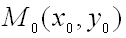 , т.е. при
, т.е. при 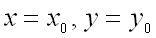 , если
, если 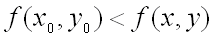 для всех точек
для всех точек 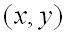 , достаточно близких к точке
, достаточно близких к точке 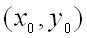 и отличных от неё.
и отличных от неё.
Максимум и минимум функции называются экстремумами функции.
Теорема (необходимое условие экстремума функции двух переменных). Если функция 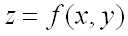 достигает экстремума при
достигает экстремума при 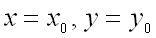 , то каждая частная производная первого порядка от
, то каждая частная производная первого порядка от 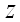 или обращается в нуль при этих значениях аргументов, или не существует.
или обращается в нуль при этих значениях аргументов, или не существует.
Теорема (достаточное условие экстремума функции двух переменных). Пусть в некоторой области, содержащей точку 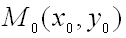 функция
функция 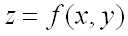 имеет непрерывные частные производные до третьего порядка включительно. Пусть, кроме того, точка
имеет непрерывные частные производные до третьего порядка включительно. Пусть, кроме того, точка 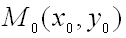 является критической точкой функции
является критической точкой функции 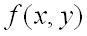 , т.е.
, т.е.
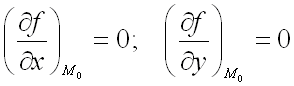 ,
,
тогда при 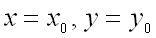 :
:
1) 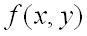 имеет максимум, если дискриминант
имеет максимум, если дискриминант 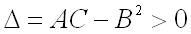 и
и 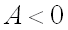 , где
, где 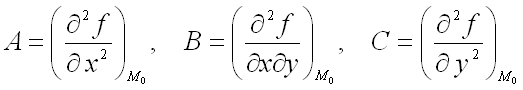 ;
;
2) 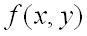 имеет минимум, если дискриминант
имеет минимум, если дискриминант 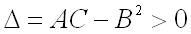 и
и 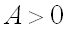 ;
;
3) 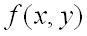 не имеет ни минимума, ни максимума, если дискриминант
не имеет ни минимума, ни максимума, если дискриминант 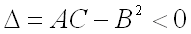 ;
;
4) если 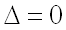 , то экстремум может быть, а может и не быть (требуется дополнительное исследование).
, то экстремум может быть, а может и не быть (требуется дополнительное исследование).
Дифференциальным уравнением первого порядка называется уравнение вида F(x, y, y ′ ) = 0, в котором x — независимая переменная, y(x) — неизвестная функция. Диф- ференциальным уравнением первого порядка, разрешенным относительно производной, называется уравнение dy dx = f(x, y). Правую часть уравнения будем считать определенной на некотором открытом множестве D плоскости (x, y). Иногда уравнение записывают в виде M(x, y) dx + N(x, y) dy = 0 (0.3) и называют уравнением первого порядка, записанным в дифференциалах
Дифференциальные уравнения с разделенными переменными
Дифференциальные уравнения с разделенными переменными имеют вид f(y)dy=g(x)dx. К ним сводятся многие дифференциальные уравнения первого порядка. В общем случае решение такого уравнения — это интегрирование обеих частей:
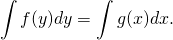
Уравнения с разделяющимися переменными Дифференциальное уравнение первого порядка y′=f(x,y) называется уравнением сразделяющимися переменными, если функцию f(x,y) можно представить в виде произведения двух функций, зависящих только от x и y: f(x,y)=p(x)h(y), где p(x) и h(y) − непрерывные функции.
Уравнение Бернулли является одним из наиболее известных нелинейных дифференциальных уравнений первого порядка. Оно записывается в видеy′+a(x)y=b(x)ym,где a(x) и b(x) − непрерывные функции.
Если m=0, то уравнение Бернулли становится линейным дифференциальным уравнением. В случае когда m=1, уравнение преобразуется в уравнение с разделяющимися переменными.
В общем случае, когда m≠0,1, уравнение Бернулли сводится к линейному дифференциальному уравнению с помощью подстановки z=y1−m.Новое дифференциальное уравнение для функции z(x) имеет видz′+(1−m)a(x)z=(1−m)b(x)
Дифференциальное уравнение xdy+ydx=0 является уравнением в полных дифференциалах, так как d(xy)= xdy+ydx . Поэтому xy = C есть общее решение этого уравнения. 2. Аналогично для уравнения 2xydx+x2dy=0 выражение x2y=C есть общее решение, так как левая часть этого уравненияявляется дифференциалом функции u(x,y)=x2y .
| Дифференциальные уравнения, допускающие понижение порядка |
| В общем случае дифференциальное уравнение второго порядка можно записать в видеF(x,y,y′,y′′)=0,где F − заданная функция указанных аргументов. Если дифференциальное уравнение можно разрешить относительно второй производной y′′, то его можно представить в следующем явном виде:y′′=f(x,y,y′).В частных случаях функция f в правой части может содержать лишь одну или две переменных. Такие неполные уравнения включают в себя 5 различных типов:y′′=f(x),y′′=f(y),y′′=f(y′),y′′=f(x,y′),y′′=f(y,y′).С помощью определенных подстановок эти уравнения можно преобразовать в уравнения первого порядка. В случае произвольных дифференциальных уравнений второго порядка, их порядок можно понизить, если эти уравнения обладают определенной симметрией. Ниже мы обсудим 2 типа таких уравнений (случаи 6 и 7): · Функция F(x,y,y′,y′′) является однородной функцией аргументов y,y′,y′′; · Функция F(x,y,y′,y′′) является точной производной функции первого порядка Φ(x,y,y′). |
Типы дифференциальных уравнений Перечислены основные типы обыкновенных дифференциальных уравнений (ДУ), допускающие решение. Для каждого типа указана ссылка на страницу, содержащую метод решения и подробные примеры. См. также: Дифференциальные уравнения – основные определения, классификация и свойства их решений Линейные дифференциальные уравнения в частных производных первого порядка Далее в тексте  - функции своих аргументов. Штрих ' означает производную по аргументу. - функции своих аргументов. Штрих ' означает производную по аргументу. 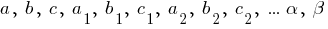 - постоянные. Дифференциальные уравнения первого порядка Особенности дифференциальных уравнений первого порядка При решении уравнений первого порядка функцию y и переменную x следует считать равноправными. То есть решение может быть в виде y(x) так и в виде x(y). Дифференциальные уравнения первого порядка, разрешенные относительно производной Уравнения с разделяющимися переменными - постоянные. Дифференциальные уравнения первого порядка Особенности дифференциальных уравнений первого порядка При решении уравнений первого порядка функцию y и переменную x следует считать равноправными. То есть решение может быть в виде y(x) так и в виде x(y). Дифференциальные уравнения первого порядка, разрешенные относительно производной Уравнения с разделяющимися переменными 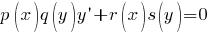 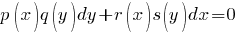 Подробнее >>> Уравнения, приводящиеся к уравнениям с разделяющимися переменными Подробнее >>> Уравнения, приводящиеся к уравнениям с разделяющимися переменными 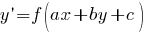 Подробнее >>> Однородные уравнения Подробнее >>> Однородные уравнения 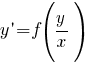 Подробнее >>> Уравнения, приводящиеся к однородным Подробнее >>> Уравнения, приводящиеся к однородным 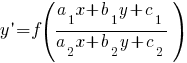 Подробнее >>> Обобщенные однородные уравнения Подробнее >>> Обобщенные однородные уравнения 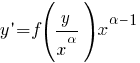 Подробнее >>> Линейные дифференциальные уравнения Подробнее >>> Линейные дифференциальные уравнения
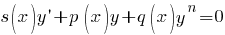 Подробнее >>> Уравнения Риккати Подробнее >>> Уравнения Риккати 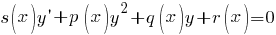 Подробнее >>> Уравнения Якоби Подробнее >>> Уравнения Якоби 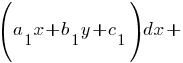 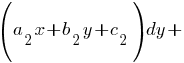 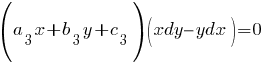 Подробнее >>> Уравнения в полных дифференциалах Подробнее >>> Уравнения в полных дифференциалах 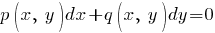 при условии при условии 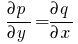 |
/