Сложение и вычитание многозначных чисел

Сложение и вычитание многозначных чисел, кроме случаев, .к.манных выше, выполняется приемами письменных вычислений. !(>< повой алгоритмов сложения и вычитания чисел любого класса |ииляется поразрядное сложение и вычитание.

Казалось бы, между сложением и вычитанием трехзначных и Многозначных чисел нет существенной разницы. Однако наблюде­ния и анализ ученических работ показывают, что чем больше числа, т. е. чем больше в них знаков, тем труднее они оказывают­ся для умственно отсталых школьников, тем больше ошибок они допускают в действиях с этими числами. Одной из причин ошибок 6 примерах с многозначными числами является неустойчивость внимания, быстрая утомляемость учащихся.

При подборе примеров надо соблюдать такой порядок:

1) на первом этапе выполняются действия сложения и вычита-
|ния без перехода через разряд;

2) на втором этапе выполняются действия с переходом через
[разряд в одном, затем в двух и более разрядах;

3) на третьем этапе выполняются действия на вычитание, в
которых уменьшаемое содержит один или несколько нулей или
нули в уменьшаемом чередуются с единицами:

97 000-378;

801 010-57 528.

Для учащихся оказываются неодинаковыми по трудности при­меры с различным количеством знаков в слагаемых. Примеры, в которых меньше знаков содержит первое слагаемое, чем второе, вызывают больше трудностей, чем примеры, в которых меньше знаков содержит второе слагаемое, чем первое, или примеры с одинаковым числом знаков (424 735+102 524). Это относится и к вычитанию.

При сложении и вычитании соблюдается поклассная и пораз­рядная запись чисел в столбик. Сложение и вычитание произво­дятся поразрядно, начиная с единиц первого класса. Например:

385 457 4425 381 132

355 784

12 115

367 899

Перова М. Н.

На первых уроках надо требовать от учащихся объяснен! поразрядного сложения и вычитания, т. е. объяснения того, кг разрядные единицы складываются или вычитаются. Затем объя нение свертывается.

Перед решением примеров на сложение и вычитание с перех дом через разряд необходимо проводить подготовительные упраж нения, которые облегчат письменные вычисления. Например:

7 ед. + 8 ед. = 15 ед. 5 дес.+8 дес. = 13 дес. 6 сот.+9 сот. = 15 сот. 10 ед. — это 1 дес. 10 ед. тыс. — это 1 дес. тыс. 10 сот. тыс. — это 1 млн

15 ед. — это 5 ед. и 1 дес.

13 дес. — это 3 ед. и 1 дес.

15 сот. — это 5 сот. и 1 тыс

10 дес. — это 1 сот.

10 сот. — это 1 тыс.

10 дес. тыс. — это 1 сот. тыс

Приводим рассуждения, которыми сопровождается решение числовых выражений на сложение и вычитание с переходом чере:< разряд:

К 5 ед. прибавим 6 ед., получим 11 ед. 11 ед. — это 1 ед. и 1 дес. 1 ед. запишем под единицами, 1 дес. прибавим к десяткам. К 4 дес. прибавим 5 дес., получим 9 дес. К 9 дес. прибавим 1 дес., получим 10 дес. 10 дес. — это 0 дес. и 1 сот. 0 дес. запишем под десятками, а 1 сот. прибавим к сотням и т. д.

37 845

283 405 ' 1 748 281 657

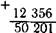От 5 ед. нельзя от нять 8 ед. Занимаем 1 дес., но десятков нет в уменьшаемом Занимаем 1 сот. и дробим ее в десят ки. В сотне 10 дес. 1 дес. зани маем и дробим его в единицы. Над десятками и над сотнями ставим точки. 1 дес. и 5 ед. — это 15 ед. Вычитаем 8 ед. из 15 ед. и получаем 7 ед. Записы­ваем 7 ед. под единицами. Из 9 дес. вычитаем 4 дес., получаем 5 дес. 5 дес. записываем под де­сятками и т. д.

Особого внимания заслуживают случаи, в которые входят сла­гаемые, содержащие нули, или случаи, в ответах которых получа­ются нули в одном или нескольких разрядах.

Например:

58475 1 526

,350007 ,355736

"*" 125 080 ⁺ 4 572

475 087

Выполняя действие вычитания, в котором уменьшаемое содер-11 несколько нулей подряд, надо вспомнить решение случаев ида 500-235, 1000-384.

Трудность выполнения действий возрастает по мере увеличения

|цсла нулей в уменьшаемом (40 457-6750; 40 007-6750; 40 000-

-0750; 40 107-6750; 40 100-6750). Особенно трудны случаи (пос-

И'дыие два), в которых в уменьшаемом нули перемежаются со знача-

Лцими цифрами. При их решении умственно отсталые учащиеся пере-

Мюсят без изменения свой опыт выполнения действий на вычитание

чисел, в которых нули в уменьшаемом были расположены подряд:

10 10 10 ' 16 756 23 344

Ю 10 10

' 16 756

Во втором примере к 9 сотням учащиеся не прибавляют 1 сотню и вычитают 7 сотен не из 10 сотен, а из 9 сотен.

Выполнение действий сложения и вычитания с двумя компо­нентами сопровождается проверкой обратными действиями, кроме этого, сложение проверяется перестановкой слагаемых, а вычита­ние — не только сложением, но и вычитанием. Проверка дейст­вий выполняется и на счетах.

Решаются также примеры с тремя и четырьмя компонентами вида 54 800+147 385+4768; 100 070+148 280-7525; 378 040-—275 896+178 608. В первых двух примерах учащиеся выполня­ют одно действие, а в третьем последовательно два действия. Необходимо указать на различие в записи и решении этих приме­ров.

Практическое использование сочетательного закона сложения обычно сопровождается заданием: решить наиболее удобным спо­собом (37 864+15 000+7000+4836). В этом случае учащиеся должны устно сложить 15 тыс. и 7 тыс., а затем провести пись­менно сложение трех слагаемых: 37 864+22 000+4836.

Разнообразить упражнения на сложение и вычитание можно,
предлагая задания на сравнение результатов действий, на провер­
ку правильности расстановки знаков равенств и неравенств. На­
пример, решить столбик примеров и расположить числа, получен­
ные в ответах, от большего к меньшему; выписать из ответов
четные или нечетные, простые или составные числа; проверить,
правильно ли поставлены знаки:
8* 227

38'-000-17 380>45 000-37 945 57 605+15 708=81 735-8 420

Решаются также примеры на нахождение неизвестных коми» нентов действий сложения и вычитания.

Разнообразие заданий, их вариации позволяют поддерживат • интерес к выполнению действий, повышают эффективность про цесса обучения, предупреждают вербализм.

Умножение и деление многозначных чисел

Умножение и деление многозначных чисел представляют гораз до больше трудностей, чем сложение и вычитание. Это связано с тем, что ученики нетвердо знают таблицу умножения. Даже т<-учащиеся, которые запомнили таблицу умножения, затруднялись применить ее при решении примера с многозначными числами, т. е. актуализировать свои знания и использовать их.

Трудности возникают и тогда, когда надо единицы низшего разряда перевести в высший, удержать их в памяти (умножение с переходом через разряд). Неумение долгое время сосредоточить внимание на выполнении действия приводит к тому, что учащиеся низшие разряды числа умножают правильно, а при умножении высших разрядов допускают ошибки. Неустойчивость внимания, стереотипность мышления являются нередко и причиной таких ошибок: умножая первый множитель на двузначный второй мно­житель, умственно отсталый школьник производит умножение только на единицы, т. е. находит первое неполное произведение, а на десятки умножение не производит, при этом считает, что дей­ствие им выполнено полностью.

Как и при умножении в пределах 1000, наибольшее затрудне­ние вызывают случаи, в которых в множителе нуль находится в середине или на конце (105x9, 580x4).

Умения и навыки в делении многозначных чисел, особенно на двузначное и трехзначное числа, вырабатываются с еще большим трудом. Умственно отсталым школьникам трудно, а некоторым даже непосильно самостоятельно применить алгоритм деления. Требуется помощь учителя, его наводящие вопросы, чтобы ученик все операции при делении применил последовательно и правиль­но. Особенно трудно подобрать цифру частного и устно прове­рить, подходит ли она. Например, характерная ошибка, которая 228

[тречается при делении, — неправильный выбор цифры частно-I, получение остатка больше делителя.

Умственно отсталые школьники, даже старших классов, отно-1тся к полученным ответам некритично. Они редко себя контро-_Фуют, не замечают абсурда (частное может получиться больше Делимого), полученного в ответе, и это их не смущает, не натал­кивает на мысль о неправильности выполнения деления.

Наибольшего внимания и большего количества упражнений требуют примеры, в которых в частном получаются нули, как в середине, так и на конце.

24__

33240 24

72 ~204~ 168 320 216 104 96

Примеры на умножение и деление много­значных чисел неоднородны по трудности их решения. Трудность возрастает с увеличением числа знаков во множителе и делителе, а также с увеличением числа замен крупных разрядов более мелкими. Поэтому с умножением и деле­нием надо знакомить учащихся в определенной последовательности, которая определяется на­растающей степенью трудности различных слу­чаев.

8 (ост.)

В школе VIII вида оправдала себя следующая последовательность в изучении действий умно­жения и деления:

1. Умножение и деление на 10, 100, 1000 (деление без остатка

и с остатком).

2. Умножение и деление на однозначное число.

3. Умножение и деление на круглые десятки, сотни и тысячи.

4. Умножение и деление на двузначные и трехзначные числа:

а) умножение и деление двузначного числа на двузначное;

б) умножение и деление трехзначного числа на двузначное (в
частном число десятков равно сначала 1, а затем 2 и т. д.);

в) умножение и деление четырехзначного числа на двузначное
(число сотен в частном сначала равно 1, затем 2 и т. д.);

г) деление четырехзначного числа на двузначное, когда число
сотен в делимом меньше, чем в делителе, и т. д.

Для лучшей отработки приемов осуществления этих действий, их дифференцировки, установления взаимосвязи между действия­ми на каждом этапе изучения действий сначала отрабатываются приемы умножения, а затем деления, действия сопоставляются,

показывается их взаимосвязь. Учащиеся знакомятся также с п| веркой действий.

После первоначального знакомства с алгоритмом умножени» деления необходимо дать достаточное количество вариативных |_ ражнений, для того чтобы учащиеся научились применять его к различным числам. Затем учащиеся учатся закреплять алгоритм и разных ситуациях, сначала под руководством учителя, а потом и самостоятельно.

2. Умножение и деление разрядных чисел на ^позначное число начинается с повторения этих действий [уже известными учащимся числами — умножаются и делятся: ) десятки (30x3, 80x4, 90:3); б) сотни (700x2, 800:4). Затем рассматриваются устные случаи умножения и деления единиц тысяч: 3000-2, 9000:3. Действия с этими числами сопоставляют-| си с действиями над простыми единицами:

9:3=3 9 тыс.:3=3 тыс.

3-2=6

3 тыс.-2=6 тыс.

и деление разрядных 20 000:4 800 000:4

Умножение и деление многозначных чиселна однозначное число

Последовательность выполнения действий:

1. Подготовительные упражнения.

2. Умножение и деление разрядных чисел на однозначное
число.

3. Умножение и деление многозначных чисел на однозначные
без раздробления и превращения разрядных единиц (12 432x2,
69 396:3).

4. Умножение и деление многозначных чисел на однозначные с
раздроблением и превращением разрядных единиц сначала в
одном, а затем в двух и более разрядах (2743-2, 42 696:3).

5. Особые случаи умножения и деления, в которых нули стоят
в середине или на конце множимого (3840 «3), делимого
(75 048:3, 42 360:3) или получаются в частном (75 130:5).

1. Подготовительные упражнения необходимы для повторения и обобщения имеющихся знаний учащихся о действи­ях умножения и деления, а также для подготовки их к более сознательному восприятию нового материала.

Необходимо повторить с учащимися, что действие умноже­ния — это нахождение суммы одинаковых слагаемых. Поэтому полезны упражнения на замену произведения суммой одинаковых слагаемых и наоборот:

8.3=8+8+8; 20+20+20+20=20-4.

Повторяется также табличное умножение и деление, умноже­ние единицы и нуля (1x7, 29x1, 0x3, 43x0), деление единицы и нуля (1:1, 0:8), деление на единицу (17:1). Учащиеся вспоми­нают названия компонентов действий умножения и деления и их результатов.

Аналогично объясняется умножение чисел в пределах 100 000 и 1 000 000.

30 000 • 3 300 000 - 2

Приемами устных вычислений выполняются действия умноже­ния и деления и над круглыми числами: 15 000:5, 12 000-2, 350 000:7, 24 000-2. Действия с числами указанных выше ви­дов выполняются устно и включаются, как правило, на уроках математики в устный счет.

3. Умножение и деление многозначных чисел на однозначное число без раздробления и превращения не представляют собой ничего нового по сравнению с выполнением этих действий в пределах 1000. Поэтому эти действия также следует рассматривать как подготовительные к следующему, более трудному этапу. Нужно повторить, как подписываются числа при записи примеров в столбик, требовать подробных объ­яснений, затем объяснения свертываются (разрядные единицы не называются):

х 3

..2243

* 2

Далее учащиеся решают примеры на умножение, а затем и на деление с раздроблением и превращением разрядных единиц.