Проверка правильности построения эпюр с использованием

дифференциальных зависимостей между Q, M, j , v

Из теории изгиба балок известно, что величины Q, M, j и v связаны между собой дифференциальными зависимостями:

; ; ; .

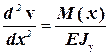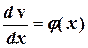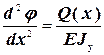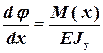На основании этих зависимостей строятся правила контроля и построения эпюр углов поворота и прогибов:

1.а) Если изгибающий момент М>0, то эпюра прогибов представляет собой

кривую, выпуклую вниз;

б) Если изгибающий момент М<0, то эпюра прогибов представляет собой

кривую, выпуклую вверх.

2.Если изгибающий момент М=0(при смене знака) или имеет скачок (при смене знака) в каком-то сечении балки, то на эпюре прогибов наблюдаем точку перегиба (т.п.).

3.Если угол поворота j =0 (при смене знака) в каком-то сечении балки, то на

эпюре прогибов наблюдаем точку экстремума (т.э.).

4.а) Если поперечная сила Q>0, то эпюра углов поворота представляет собой кривую, выпуклую вниз;

б) Если поперечная сила Q <0, то эпюра углов поворота представляет собой кривую, выпуклую вверх.

5. Если поперечная сила Q=0 (при смене знака) или имеет скачок (при смене

знака) в каком-то сечении балки, то на эпюре углов поворота наблюдаем

точку перегиба (т.п.).

6.Если изгибающий момент М=0 (при смене знака) или имеет скачок (при смене знака) в каком-то сечении балки, то на эпюре углов поворота наблюдаем точку экстремума (т.э.).

7. Если на эпюре изгибающих моментов в каком-то сечении балки наблюдается скачок, то на эпюре углов поворота наблюдаем точку излома (т.и.).

10. Для выбранного в пункте 3 типа сечения (двутавр или два швеллера) из условия жесткости определяем номер прокатного профиля, приняв допускаемый прогиб 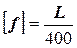, где L – длина пролета.

По эпюре прогибов (рис.3) приближенно определяем максимальное по абсолютной величине значение прогиба

| v_max|= 8,12∙10^{-3 м =} .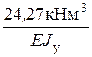

Допускаемый прогиб 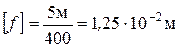, где длина пролета L=5 м.

Из условия жесткости v_max 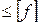определяем требуемый момент инерции

.

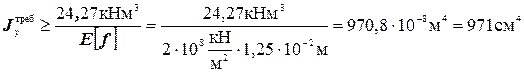Для сечения, состоящего из двух швеллеров 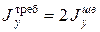, поэтому

.

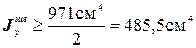По сортаменту прокатной стали выбираем швеллер № 14, т.к. его момент инерции 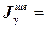491 см⁴.

Чтобы одновременно выполнялись оба условия прочности и жесткости необходимо выбрать сечение, состоящее из двух швеллеров № 16.

Задача 2. Расчет на прочность и жесткость статически неопределимой

Балки

В статически определимой балке (рис.1) заменяем левую опору жесткой заделкой. В результате получаем схему, показанную на рис.8.

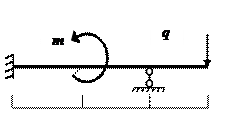Исходные данные:

a= 2 м;b= 3 м;c= 1 м;

q=15 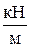;m=20 кНм;F=30 кН.

Рис.8.

Для полученной расчетной схемы статически неопределимой балки требуется:

1.Определить опорные реакции, раскрывая статическую неопределимость

методом начальных параметров.

2. Построить эпюры поперечных сил и изгибающих моментов.

3.Проверить прочность балки из прокатного профиля, подобранного в первой

задаче.

4. Вычислить значения углов поворота поперечных сечений и прогибов оси

балки в характерных точках. Построить их эпюры.

5.Определить величину максимального прогиба и проверить жесткость

балки, приняв допускаемый прогиб [f]= 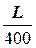, где L– длина пролета.

Статически неопределимыми являются балки, у которых число неизвестных опорных реакций превышает число независимых уравнений равновесия (уравнений статики).

Степень статической неопределимости задачи определяется как разность между количеством неизвестных опорных реакций и количеством уравнений статики.

Решение

Определение опорных реакций

Заменим действие опор A и B опорными реакциями (рис.9). В нашем примере неизвестных опорных реакций четыре: R_A, H_A, M_A, R_B ; а число независимых равнений статики – 3,

Рис.9. поэтому балка 1 раз статически неопределима.

а) Статическая сторона задачи

; .

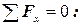
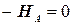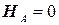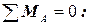-M_A+ m - q·3(2+1, 5) + R_B·5-F·6 =0;

- M_A + 20- 15·3·3, 5 + R_B·5- 30·6 =0;

- M_A+ R_B·5 =317, 5. (5)

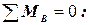- M_A- R_A·5+ m + q·3·1, 5- F·1 =0;

-M_A- R_A·5 + 20 +15·4, 5 -30 =0;

M_A+ R_A·5 =57, 5 . (6)

Получено два независимых уравнения статики - (5) и (6) относительно трех неизвестных опорных реакций.

б) Геометрическая сторона задачи - кинематические граничные условия

На опоре A: v_A= 0; j _A = 0;

На опоре B : v_B= v(5) =0. (7)

в) Физическая сторона задачи - уравнение метода начальных параметров, которое получено на основе закона Гука

Начальные параметры (начало отсчета на опоре A):

v₀ = v_A= 0; j ₀ = j _A = 0; M₀ = M_A; F₀ = R_A,

поэтому уравнение метода начальных параметров для прогиба имеет следующий вид:

Iучасток: 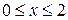IIучасток: 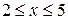IIIучасток: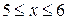

v(x) = 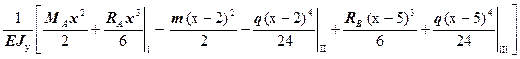.(8)

Последнее выражение (8) отличается от выражения (3) для прогиба только изменением значений начальных параметров. Теперь j ₀ =0; M₀= M_A.

Используя граничное условие (7) (прогиб на опоре B равен нулю) и выражение (8), получаем дополнительное уравнение (уравнение деформаций) для определения опорных реакций

v_B=v (5) = .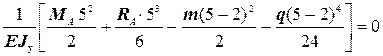

Подставляя в полученное уравнение значения m и q, получаем

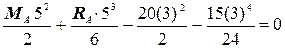½× ;

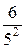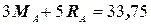. (9)

Уравнения (5),(6),(9) образуют систему трех уравнений относительно неизвестных опорных реакций R_A, M_A, R_B:

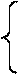- M_A+ 5R_B =317, 5 ;

M_A + 5R_A=57, 5 ; (10)

3 M_A + 5R_A=33, 75 .

Вычитая из третьего уравнения системы (10) второе, определяем M_A:

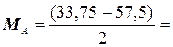-11,875 кНм = -11, 9 кНм.

Из второго уравнения системы (10) находим R_A

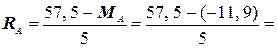13, 88 кН =13, 9 кН.

Из третьего уравнения системы (10) находим R_B:

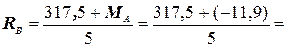61,12 кН =61, 1 кН.

После определения опорных реакций необходимо сделать несколько проверок:

а) проверка правильности решения системы уравнений (10)

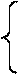- M_A+ 5R_B-317, 5=0? -(-11, 9) + 5∙61, 1- 317, 5 = 317, 4-317, 5 = 0, 1 = 0;

M_A + 5R_A -57, 5=0? (-11, 9) + 5∙13, 9- 57, 5 = 57, 6-57, 5 = 0, 1 = 0;

3M_A + 5R_A-33, 75=0? 3∙ (-11, 9) + 5∙13, 9- 33, 75 = 33, 8-33, 75 = 0, 05 = 0.

б) статическая проверка (сумма проекций всех сил на вертикальную ось z должна быть равна 0)

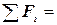R_A - q·3 + R_B- F = 13, 9 - 15·3 + 61, 1 - 30 = 75 - 75=0.

в) кинематическая проверка (прогиб на опоре B должен быть равен нулю)

v _B=v (5) =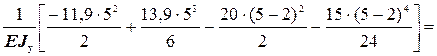

.

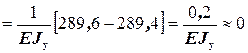Проверки показывают, что опорные реакции найдены правильно.

2.Построение эпюр поперечной силы Q и изгибающего момента M

RA=13,9кН

HA=0

B

A

RB=61,1кН

x3

MA=- 11,9кНм

1м

3м

2м

m=20кНм

x1

x2

Рис.10.

I участок ;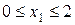

Q(x₁) = R_A =13, 9 кН;

M(x₁)= M_A+ R_A x₁ = – 11, 9+13, 9x₁;

M (0) = – 11, 9 кНм; M(2)= = – 11, 9+13, 9·2=15, 9 кНм.

II участок ;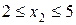

Q(x₂) = R_A– q(x₂- 2) = 13, 9- 15(x₂- 2) =43, 9- 15x₂;

Q (2) = 43, 9- 30=13, 9 кН;

Q (5) = 43, 9 -15·5= -31, 1 кН .

Поскольку поперечная сила меняет знак в пределах участка, определяем координату, при которой она обращается в нуль:

Q(x₀) = 43, 9- 15x₀=0; x₀= 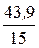=2,93 м;

M(x₂) = M_A +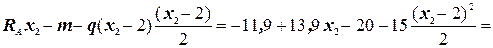

=-31, 9 + 13, 9x₂ - 7, 5(x₂-2)²;

M (2) = -31, 9 + 13, 9∙2 - 7, 5(2-2)²= 4, 1кНм;

M(2, 93) = -31, 9 + 13, 9∙2, 93 - 7, 5(2, 93-2)²= 2, 34кНм;

M(5) = -31, 9 + 13, 9∙5 - 7, 5(5 - 2)²= - 29, 9кНм = – 30 кНм.

III участок 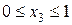(начало отсчета на правом конце);

Q(x₃) = F= 30 кН;

M(x₃) = – F x₃ = - 30x₃; M(0)= 0 кНм; M(1)= - 30 кНм.

Используя полученные значения, строим в масштабе эпюры поперечных сил и изгибающих моментов, как показано на рис.11.

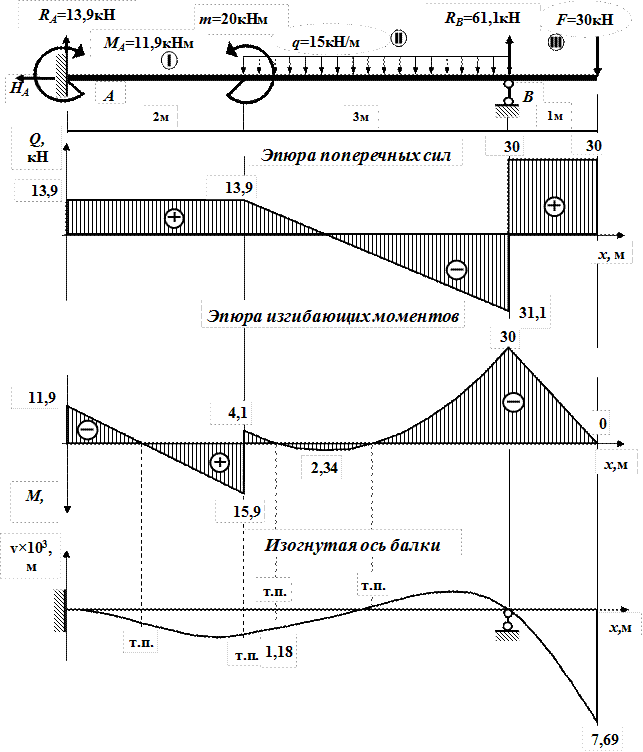
Рис.11.