Задача 1. Расчет на прочность и жесткость статически определимой балки

Утверждено на заседании

кафедры сопротивления

материалов 6 декабря 2012 г.

МЕТОДИЧЕСКИЕ УКАЗАНИЯ

по выполнению расчетно-графической работы

по дисциплине «Сопротивление материалов»

«РАСЧЕТ БАЛОК НА ПРОЧНОСТЬ И ЖЕСТКОСТЬ»

(для бакалавров и специалистов)

Ростов-на-Дону

2013 г.

УДК 620.178.32 (076.5)

Методические указания по выполнению расчетно-графической работы

по дисциплине «Сопротивление материалов» «Расчет балок на прочность и жесткость». – Ростов н/Д: Рост. гос. строит. ун-т, 2013. – 23с.

Методические указания содержат теоретические положения, примеры и порядок выполнения студентами расчетно-графической работы по сопротивлению материалов «Расчет балок на прочность и жесткость». Методические указания предназначены для бакалавров и специалистов, следующих направлений подготовки(специальностей): 270800 «Строительство», 270200 «Реконструкция и реставрация», 230400 «Информационные системы и технологии», 221700 «Стандартизация и метрология», 190600 «Эксплуатация транспортных машин и комплексов»

УДК 620.178.32 (076.5)

Составители: канд. техн. наук, проф.Краснобаев И.А.

канд. физ.-мат. наук, доц.Стрельников Г.П.

канд. техн. наук, доц. Бондаренко В.П.

Редактор М.А. Нестеренко

Темплан 2013г., поз.110

Подписано в печать 11.01.13. Формат 60х84/16

Бумага писчая. Ризограф. Уч.-изд.л. 1,0.

Тираж 200 экз. Заказ

Редакционно-издательский центр

Ростовского государственного строительного университета.

344022, Ростов-на-Дону, Социалистическая, 162.

© Ростовский государственный

строительный университет,2013

В расчетно-графической работе «Расчет балок на прочность и жесткость» студенту предлагается выполнить расчет двух типов балок.

Задача 1. Расчет на прочность и жесткость статически определимой балки

Для заданной расчетной схемы балки на двух опорах (рис.1) требуется:

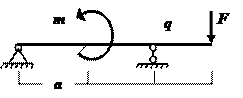Исходные данные:

a=2 м; b=3 м; c=1 м;

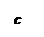q=15 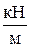;m=20 кНм; F=30 кН.

Рис.1.

1.Определить опорные реакции.

2.Для каждого участка балки, используя метод сечений, составить выра-

жения поперечных сил (Q) и изгибающих моментов(M). Построить их

эпюры.

3.Из условия прочности по методу допускаемых напряжений подобрать

сечение балки из двутавра или двух швеллеров, приняв допускаемое

нормальное напряжение [s]=160МПа.

4. Проверить прочность балки по касательным напряжениям, приняв

допускаемое касательное напряжение [t] =0,6[s ].

5.Составить выражения для прогибов и углов поворота поперечных сече-

ний по методу начальных параметров.

6.Определить начальный угол поворота из условия закрепления балки на

правом шарнире.

7.Найти значение жесткости поперечного сечения (ЕJ _y).

8.Вычислить значения углов поворота поперечных сечений и прогибов

оси балки в характерных точках. Построить их эпюры.

9.Проверить правильность построения эпюр, используя дифференциаль-

ные зависимости между Q, M, j , v .

10. Для выбранного в пункте 3 типа сечения (двутавр или два швеллера) из

условия жесткости определить номер прокатного профиля, приняв

допускаемый прогиб [ f ]= 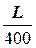, где L – длина пролета.

Решение

Определение опорных реакций

Для балки, изображенной на рис.2, составляем три уравнения статики:

; .

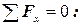
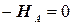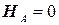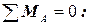m - q·3(2+1, 5) + R_B·5- F·6 =0;

20- 15·3·3, 5 + R_B·5- 30·6 =0;

20- 157, 5 + R_B·5- 180 =0;

-317, 5 + R_B·5=0; R_B= 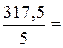63, 5 кН.

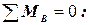- R_A·5+ m + q·3·1, 5- F·1 =0;

- R_A·5 + 20 +15·4, 5 -30 =0;

- R_A·5 + 20 +67, 5 - 30 =0;

-R_A·5 + 57, 5 =0; R_A= 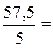11, 5 кН.

Построение их эпюр

HA=0

2м

RB=63,5кН

A

1м

3м

m=20кНм

B

RA=11,5кН

x3

x1

x2

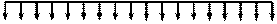
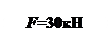
Рис.2.

I участок ;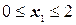

Q(x₁) = R_A=11, 5 кН;

M(x₁) = R_A x₁ = 11, 5 x₁;

M (0) =0; M (2) = 11, 5·2=23 кНм.

II участок ;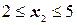

Q(x₂) = R_A– q(x₂- 2) = 11, 5- 15(x₂- 2) =41, 5- 15x₂;

Q (2) = 41, 5- 30=11, 5 кН;

Q (5) = 41, 5 -15·5=41, 5 -75 = -33, 5 кН.

Поскольку поперечная сила меняет знак в пределах участка, определяем координату, при которой она обращается в нуль (напоминаем, что в этом сечении изгибающий момент принимает экстремальное значение):

Q(x₀) = 41, 5- 15x₀=0; x₀= 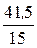=2, 77 м;

M(x₂) =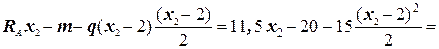

;

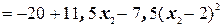M (2) = 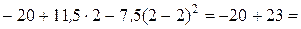3 кНм;

M (2, 77) = 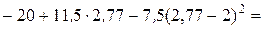7,408 кНм = 7, 41 кНм;

M (5) = 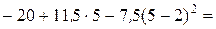– 30 кНм.

III участок 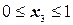(начало отсчета на правом конце);

Q(x₃) = F= 30 кН;

M(x₃) = – F x₃ = - 30x₃ ;

M(0) = 0 кНм;

M(1) = - 30 кНм.

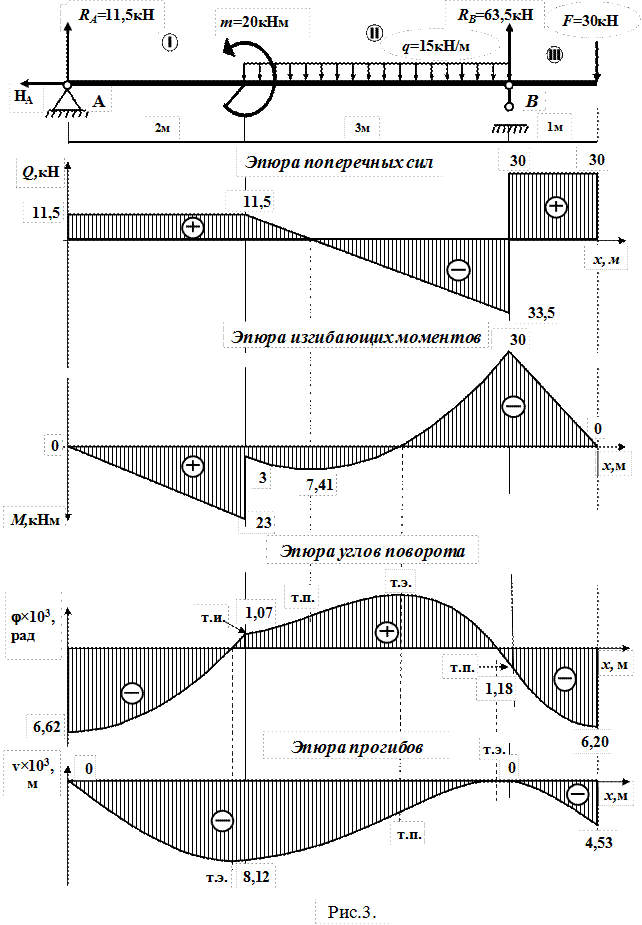
Используя полученные значения, строим в масштабе эпюры поперечных сил и изгибающих моментов, как показано на рис.3.

Допускаемых напряжений

Условие прочности при изгибе по нормальным напряжениям по методу допускаемых напряжений имеет вид:

s_max 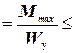[s] (1)

В этой формуле:

s_max - максимальное нормальное напряжение;

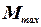- максимальное по абсолютной величине значение изгибающего

момента (определяется по эпюре изгибающих моментов);

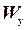- момент сопротивления относительно оси y;

[s] - допускаемое нормальное напряжение.

В опасном сечении по нормальным напряжениям (сечение, проходящее через опору B на рис.3)

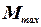=30 кНм = 30×10^-3 МНм.

Из условия прочности (1) определяем требуемую величину момента сопротивления:

.

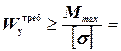
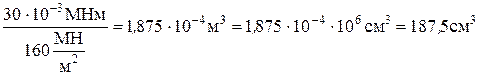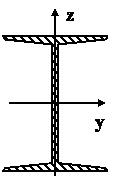
Выполним подбор профиля двутаврового сечения (рис.4). По сортаменту прокатной стали ближайшим к 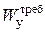является значение момента сопротивления 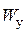=184 см³, которое соответствует двутавру №20.

Итак, для двутавра №20 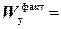184см³=184·10^{-6 м3} проверяем выполнение условия прочности:

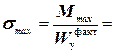
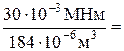163 МПа> [s] =160 МПа.

Полученный результат показывает, что балка перегружена.

Определяем величину перегрузки:

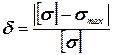×100 % 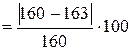%=1,88 % .

Рис.4.

Величина перегрузки не превышает 5%, что допустимо при расчете по методу допускаемых напряжений.

Проведем подбор сечения, состоящего из двух швеллеров (рис.5).

Момент сопротивления одного швеллера должен удовлетворять условию

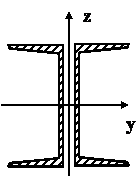
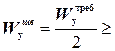
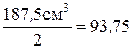см³.

Здесь индексом “шв”обозначается момент сопротивления одного швеллера.

По сортаменту прокатной стали выбираем швеллер № 16, т.к. его момент сопротивления 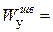93,4 см³, тогда

Рис.5. 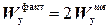=2·93,4 см³=186,8 см³=186,8 ·10^{-6 м3}.

Для выбранного сечения проверяем выполнение условия прочности: 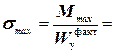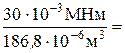160,60 МПа =161 МПа > [s] =160 МПа.

Последнее условие показывает, что балка перегружена и, очевидно, что величина перегрузки не превышает 5%, поэтому можно выбрать сечение, состоящее из двух швеллеров №16.

Оба профиля перегружены, но первый ( 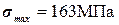) перегружен больше, чем второй ( 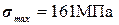). Поэтому окончательно выбираем сечение, состоящее из двух швеллеров № 16.

Балки

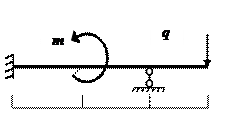
В статически определимой балке (рис.1) заменяем левую опору жесткой заделкой. В результате получаем схему, показанную на рис.8.

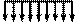
Исходные данные:

a= 2 м;b= 3 м;c= 1 м;

q=15 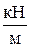;m=20 кНм;F=30 кН.

Рис.8.

Для полученной расчетной схемы статически неопределимой балки требуется:

1.Определить опорные реакции, раскрывая статическую неопределимость

методом начальных параметров.

2. Построить эпюры поперечных сил и изгибающих моментов.

3.Проверить прочность балки из прокатного профиля, подобранного в первой

задаче.

4. Вычислить значения углов поворота поперечных сечений и прогибов оси

балки в характерных точках. Построить их эпюры.

5.Определить величину максимального прогиба и проверить жесткость

балки, приняв допускаемый прогиб [f]= 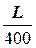, где L– длина пролета.

Статически неопределимыми являются балки, у которых число неизвестных опорных реакций превышает число независимых уравнений равновесия (уравнений статики).

Степень статической неопределимости задачи определяется как разность между количеством неизвестных опорных реакций и количеством уравнений статики.

Решение

Определение опорных реакций

Заменим действие опор A и B опорными реакциями (рис.9). В нашем примере неизвестных опорных реакций четыре: R_A, H_A, M_A, R_B ; а число независимых равнений статики – 3,

Рис.9. поэтому балка 1 раз статически неопределима.

а) Статическая сторона задачи

; .

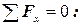
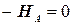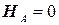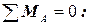-M_A+ m - q·3(2+1, 5) + R_B·5-F·6 =0;

- M_A + 20- 15·3·3, 5 + R_B·5- 30·6 =0;

- M_A+ R_B·5 =317, 5. (5)

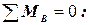- M_A- R_A·5+ m + q·3·1, 5- F·1 =0;

-M_A- R_A·5 + 20 +15·4, 5 -30 =0;

M_A+ R_A·5 =57, 5 . (6)

Получено два независимых уравнения статики - (5) и (6) относительно трех неизвестных опорных реакций.

б) Геометрическая сторона задачи - кинематические граничные условия

На опоре A: v_A= 0; j _A = 0;

На опоре B : v_B= v(5) =0. (7)

в) Физическая сторона задачи - уравнение метода начальных параметров, которое получено на основе закона Гука

Начальные параметры (начало отсчета на опоре A):

v₀ = v_A= 0; j ₀ = j _A = 0; M₀ = M_A; F₀ = R_A,

поэтому уравнение метода начальных параметров для прогиба имеет следующий вид:

Iучасток: 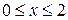IIучасток: 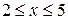IIIучасток: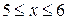

v(x) = 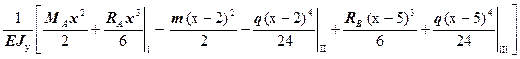.(8)

Последнее выражение (8) отличается от выражения (3) для прогиба только изменением значений начальных параметров. Теперь j ₀ =0; M₀= M_A.

Используя граничное условие (7) (прогиб на опоре B равен нулю) и выражение (8), получаем дополнительное уравнение (уравнение деформаций) для определения опорных реакций

v_B=v (5) = .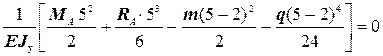

Подставляя в полученное уравнение значения m и q, получаем

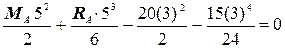½× ;

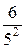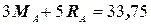. (9)

Уравнения (5),(6),(9) образуют систему трех уравнений относительно неизвестных опорных реакций R_A, M_A, R_B:

- M_A+ 5R_B =317, 5 ;

M_A + 5R_A=57, 5 ; (10)

3 M_A + 5R_A=33, 75 .

Вычитая из третьего уравнения системы (10) второе, определяем M_A:

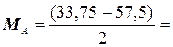-11,875 кНм = -11, 9 кНм.

Из второго уравнения системы (10) находим R_A

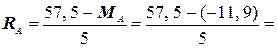13, 88 кН =13, 9 кН.

Из третьего уравнения системы (10) находим R_B:

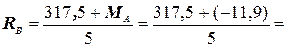61,12 кН =61, 1 кН.

После определения опорных реакций необходимо сделать несколько проверок:

а) проверка правильности решения системы уравнений (10)

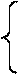- M_A+ 5R_B-317, 5=0? -(-11, 9) + 5∙61, 1- 317, 5 = 317, 4-317, 5 = 0, 1 = 0;

M_A + 5R_A -57, 5=0? (-11, 9) + 5∙13, 9- 57, 5 = 57, 6-57, 5 = 0, 1 = 0;

3M_A + 5R_A-33, 75=0? 3∙ (-11, 9) + 5∙13, 9- 33, 75 = 33, 8-33, 75 = 0, 05 = 0.

б) статическая проверка (сумма проекций всех сил на вертикальную ось z должна быть равна 0)

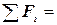R_A - q·3 + R_B- F = 13, 9 - 15·3 + 61, 1 - 30 = 75 - 75=0.

в) кинематическая проверка (прогиб на опоре B должен быть равен нулю)

v _B=v (5) =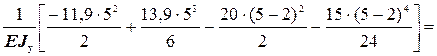

.

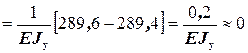Проверки показывают, что опорные реакции найдены правильно.

2.Построение эпюр поперечной силы Q и изгибающего момента M

RA=13,9кН

HA=0

B

A

RB=61,1кН

x3

MA=- 11,9кНм

1м

3м

2м

m=20кНм

x1

x2

Рис.10.

I участок ;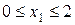

Q(x₁) = R_A =13, 9 кН;

M(x₁)= M_A+ R_A x₁ = – 11, 9+13, 9x₁;

M (0) = – 11, 9 кНм; M(2)= = – 11, 9+13, 9·2=15, 9 кНм.

II участок ;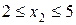

Q(x₂) = R_A– q(x₂- 2) = 13, 9- 15(x₂- 2) =43, 9- 15x₂;

Q (2) = 43, 9- 30=13, 9 кН;

Q (5) = 43, 9 -15·5= -31, 1 кН .

Поскольку поперечная сила меняет знак в пределах участка, определяем координату, при которой она обращается в нуль:

Q(x₀) = 43, 9- 15x₀=0; x₀= 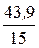=2,93 м;

M(x₂) = M_A +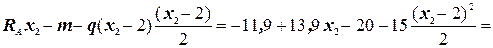

=-31, 9 + 13, 9x₂ - 7, 5(x₂-2)²;

M (2) = -31, 9 + 13, 9∙2 - 7, 5(2-2)²= 4, 1кНм;

M(2, 93) = -31, 9 + 13, 9∙2, 93 - 7, 5(2, 93-2)²= 2, 34кНм;

M(5) = -31, 9 + 13, 9∙5 - 7, 5(5 - 2)²= - 29, 9кНм = – 30 кНм.

III участок 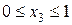(начало отсчета на правом конце);

Q(x₃) = F= 30 кН;

M(x₃) = – F x₃ = - 30x₃; M(0)= 0 кНм; M(1)= - 30 кНм.

Используя полученные значения, строим в масштабе эпюры поперечных сил и изгибающих моментов, как показано на рис.11.

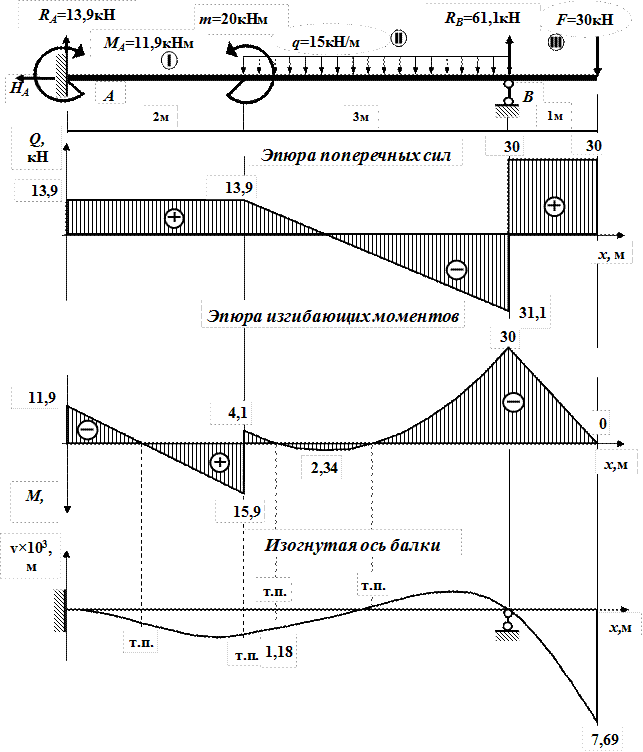
Рис.11.

Утверждено на заседании

кафедры сопротивления

материалов 6 декабря 2012 г.

МЕТОДИЧЕСКИЕ УКАЗАНИЯ

по выполнению расчетно-графической работы

по дисциплине «Сопротивление материалов»

«РАСЧЕТ БАЛОК НА ПРОЧНОСТЬ И ЖЕСТКОСТЬ»

(для бакалавров и специалистов)

Ростов-на-Дону

2013 г.

УДК 620.178.32 (076.5)

Методические указания по выполнению расчетно-графической работы

по дисциплине «Сопротивление материалов» «Расчет балок на прочность и жесткость». – Ростов н/Д: Рост. гос. строит. ун-т, 2013. – 23с.

Методические указания содержат теоретические положения, примеры и порядок выполнения студентами расчетно-графической работы по сопротивлению материалов «Расчет балок на прочность и жесткость». Методические указания предназначены для бакалавров и специалистов, следующих направлений подготовки(специальностей): 270800 «Строительство», 270200 «Реконструкция и реставрация», 230400 «Информационные системы и технологии», 221700 «Стандартизация и метрология», 190600 «Эксплуатация транспортных машин и комплексов»

УДК 620.178.32 (076.5)

Составители: канд. техн. наук, проф.Краснобаев И.А.

канд. физ.-мат. наук, доц.Стрельников Г.П.

канд. техн. наук, доц. Бондаренко В.П.

Редактор М.А. Нестеренко

Темплан 2013г., поз.110

Подписано в печать 11.01.13. Формат 60х84/16

Бумага писчая. Ризограф. Уч.-изд.л. 1,0.

Тираж 200 экз. Заказ

Редакционно-издательский центр

Ростовского государственного строительного университета.

344022, Ростов-на-Дону, Социалистическая, 162.

© Ростовский государственный

строительный университет,2013

В расчетно-графической работе «Расчет балок на прочность и жесткость» студенту предлагается выполнить расчет двух типов балок.

Задача 1. Расчет на прочность и жесткость статически определимой балки

Для заданной расчетной схемы балки на двух опорах (рис.1) требуется:

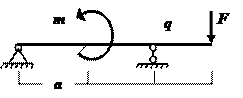Исходные данные:

a=2 м; b=3 м; c=1 м;

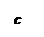q=15 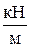;m=20 кНм; F=30 кН.

Рис.1.

1.Определить опорные реакции.

2.Для каждого участка балки, используя метод сечений, составить выра-

жения поперечных сил (Q) и изгибающих моментов(M). Построить их

эпюры.

3.Из условия прочности по методу допускаемых напряжений подобрать

сечение балки из двутавра или двух швеллеров, приняв допускаемое

нормальное напряжение [s]=160МПа.

4. Проверить прочность балки по касательным напряжениям, приняв

допускаемое касательное напряжение [t] =0,6[s ].

5.Составить выражения для прогибов и углов поворота поперечных сече-

ний по методу начальных параметров.

6.Определить начальный угол поворота из условия закрепления балки на

правом шарнире.

7.Найти значение жесткости поперечного сечения (ЕJ _y).

8.Вычислить значения углов поворота поперечных сечений и прогибов

оси балки в характерных точках. Построить их эпюры.

9.Проверить правильность построения эпюр, используя дифференциаль-

ные зависимости между Q, M, j , v .

10. Для выбранного в пункте 3 типа сечения (двутавр или два швеллера) из

условия жесткости определить номер прокатного профиля, приняв

допускаемый прогиб [ f ]= 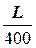, где L – длина пролета.

Решение

Определение опорных реакций

Для балки, изображенной на рис.2, составляем три уравнения статики:

; .

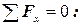
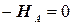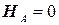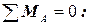m - q·3(2+1, 5) + R_B·5- F·6 =0;

20- 15·3·3, 5 + R_B·5- 30·6 =0;

20- 157, 5 + R_B·5- 180 =0;

-317, 5 + R_B·5=0; R_B= 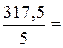63, 5 кН.

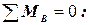- R_A·5+ m + q·3·1, 5- F·1 =0;

- R_A·5 + 20 +15·4, 5 -30 =0;

- R_A·5 + 20 +67, 5 - 30 =0;

-R_A·5 + 57, 5 =0; R_A= 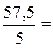11, 5 кН.