Достоверность статистических показателей

В лесохозяйственных исследованиях, связанных в основном со случайными событиями возникает необходимость характеризовать процессы и явления с определенной степенью достоверности. Для этого важно оперировать понятием ошибок и точности определения средних величин и других статистических показателей. Ошибки, по которым дается оценка достоверности называются ошибками репрезентативности, а. иными словами представительности.

Предельной ошибкой выборочного наблюдения 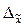называется разность между величиной средней в генеральной совокупности и ее величиной, вычисленной по результатам выборочного наблюдения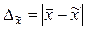

В теореме известного математика П.Л. Чебышева доказано, что величина предельной ошибки выборки не должна превышать соотношения

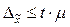, (2.20)

где величина μ, называется средним квадратическим отклонением выборочной средней от генеральной средней и определяется по зависимости

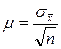(2.21)

где 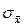- среднее квадратическое отклонение в генеральной совокупности;

n – число наблюдений.

t – коэффициент доверия, параметр, указывающий на конкретное значение вероятности того, на какую величину генеральная средняя будет отличаться от выборочной средней.

Соотношения между дисперсиями генеральной и выборочной совокупности выражается формулой

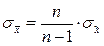(2.22)

Поскольку величина n/n-1 при достаточно больших n близка к 1, то можно приближенно считать, что выборочная и генеральные дисперсии равны. Математиком А.М. Ляпуновым составлены специальные таблицы, связывающие коэффициент доверия t с вероятностью того, что разность между выборочной и генеральной средними не превысит значения средней ошибки выборки μ.

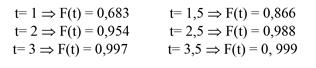
Из первой строки левого столбца видно , что с вероятностью 0,683 можно утверждать, что разность между выборочной и генеральной средними не превысит одной величины средней ошибки выборки. Или другими словами, в 68,3 % случаев ошибка репрезентативности не выйдет за пределы +- μ.. И далее видно, что чем больше пределы, в которых допускается возможная ошибка, тем с большей вероятностью судят о ее величине.

Зная выборочную среднюю величину признака 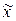и предельную ошибку выборки 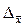, можно рассчитать границы ( пределы), в которых заключена генеральная средняя

.

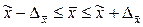Выборочные начальные и центральные моменты.

Асимметрия. Эксцесс.

Приведем краткий обзор характеристик, которые наряду с уже рассмотренными применяются для анализа статистических рядов и являются аналогами соответствующих числовых характеристик случайной величины.

Среднее выборочное и выборочная дисперсия являются частным случаем более общего понятия – момента статистического ряда.

Определение. Начальным выборочным моментом порядка называется среднее арифметическое - х степеней всех значений выборки:

или .

Из определения следует, что начальный выборочный момент первого порядка: .

Определение. Центральным выборочным моментом порядка называется среднее арифметическое -х степеней отклонений наблюдаемых значений выборки от выборочного среднего :

или .

Из определения следует, что центральный выборочный момент второго порядка:

.

Определение. Выборочным коэффициентом асимметрии называется число , определяемое формулой: .

Выборочный коэффициент асимметрии служит для характеристики асимметрии полигона вариационного ряда. Если полигон асимметричен, то одна из ветвей его, начиная с вершины, имеет более пологий «спуск», чем другая.

Если , то более пологий «спуск» полигона наблюдается слева; если - справа. В первом случае асимметрию называют левосторонней, а во втором - правосторонней.

Пример 2.10 использования функции СКОС()MSExcel для расчета асимметрии распределения. Асимметрия характеризует степень несимметричности распределения относительно его среднего. Положительная асимметрия указывает на отклонение распределения в сторону положительных значений. Отрицательная асимметрия указывает на отклонение распределения в сторону отрицательных значений.

Синтаксис: СКОС(число1;число2; …), где число1, число2, … – это от 1 до 30 аргументов, для которых вычисляется асимметричность. Можно использовать массив или ссылку на массив вместо аргументов, разделяемых точкой с запятой.

На рис. 2.8 приведено окно программы MS Excel, демонстрирующее применение функции СКОС()для определения коэффициента асимметрииА распределения толщины деревьев сосны, записанных в ячейках А2-А21 (см. пример 2.1). СКОС(A2:A21) равняется 0,55, т.е. правая ветвь растянута.

Определение. Выборочным коэффициентом эксцесса или коэффициентом крутости называется число 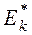, определяемое формулой:

.

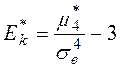Выборочный коэффициент эксцесса служит для сравнения на «крутость» выборочного распределения с нормальным распределением.

Коэффициент эксцесса для случайной величины, распределенной по нормальному закону, равен нулю.

Поэтому за стандартное значение выборочного коэффициента эксцесса принимают .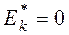

Если 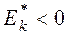, то полигон имеет более пологую вершину по сравнению с нормальной кривой; если 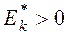, то полигон более крутой по сравнению с нормальной кривой.

Пример 2.11 использования функции ЭКСЦЕСС()MSExcel для расчета эксцесса множества данных. Эксцесс характеризует относительную остроконечность или сглаженность распределения по сравнению с нормальным распределением. Положительный эксцесс обозначает относительно остроконечное распределение. Отрицательный эксцесс обозначает относительно сглаженное распределение.

Синтаксис: ЭКСЦЕСС(число1;число2; …), где число1, число2, … – это от 1 до 30 аргументов, для которых вычисляется эксцесс. Можно использовать массив или ссылку на массив вместо аргументов, разделяемых точкой с запятой.

На рис. 2.8 приведено окно программы MS Excel, демонстрирующее применение функции ЭКСЦЕСС()для расчета показателя эксцессаЕ распределения толщин сосны, записанных в ячейках А2-А21 (см. пример 2.1). ЭКСЦЕСС(A2:A21) равняется 0,814, что говорит об островершинности кривой

Интервальные оценки

При выборке малого объема точечная оценка может существенно отличаться от оцениваемого параметра. В этом случае целесообразно использовать интервальные оценки.

Определение. Интервальной называют оценку, которая определяется двумя числами – концами интервала.

Пусть найденная по данным выборки величина 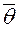служит оценкой неизвестного параметра 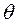. Оценка 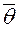определяет 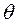тем точнее, чем меньше 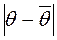, то есть чем меньше 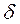в неравенстве .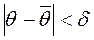

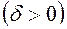Поскольку 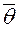- случайная величина, то и разность 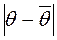- случайная величина. Поэтому неравенство 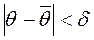, при заданном 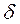может выполняться только с некоторой вероятностью.

Определение. Доверительной вероятностью (надежностью) оценки 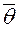параметра 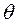называется вероятность 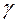, с которой выполняется неравенство .

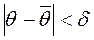Обычно задается надежность 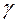и определяется 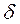. Чаще всего надежность задается значениями от 0,95 и выше, в зависимости от конкретно решаемой задачи.

Неравенство 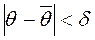можно записать .

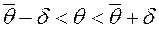Определение. Доверительным интервалом называется интервал 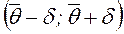, который покрывает неизвестный параметр с заданной надежностью .

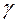Пример 2.12. Использование функции ДОВЕРИТ() MSExcel для расчета доверительного интервала для средней генеральной совокупности. Доверительный интервал – это интервал с обеих сторон от средней в выборке.

Синтаксис: ДОВЕРИТ(α; стандоткл; размер), где

α – это уровень значимости, используемый для оценки уровня надежности. Уровень надежности равняется 100(1 – α) процентам, или, другими словами, α равное 0,05 означает 95-процентный уровень надежности.

Стандоткл - это стандартное отклонение выборочной совокупности для интервала данных, предполагается известным.

Размер - это объем выборки.

· Если предположить, что альфа равняется 0,05, то нужно определить ту часть стандартной нормальной кривой, которая равняется (1 – α), или 95 процентам. Это значение из таблицы (см. приложение 1) равно 1,96. Доверительный интервал, следовательно, определяется следующим образом:

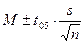(2.26)

Предположим, что при перечете 200 деревьев на пробной площади средний арифметический диаметр равен 14,4 см со стандартным отклонением 15,0 см. В таком случае, мы можем быть на 95 процентов уверены в том, что среднее для генеральной совокупности находится в интервале:

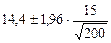
или:

ДОВЕРИТ(0,05;15;200) равняется 1,06066. Другими словами, средний диаметр генеральной совокупности равен 14,4 ± 1,06066 или от 13,3 до 15,5 см.