Классификационная скрытность
СИГНАЛОВ
8.1 Задача классификации сигналов
Различение случайных сигналов чаще всего производится по какому-либо параметру (центральной частоте, внутренней структуре, среднему значению, дисперсии и т.д.). Если явные простые признаки различия сигналов отсутствуют или не известны, то можно проводить классификацию наблюдаемых случайных процессов.
В задаче классификации все множество возможных реализаций случайного процесса разбивается на классы (группы), для которых выбраны характеристики случайных процессов - типичных представителей классов. Характеристики наблюдаемого случайного процесса сравниваются с характеристиками типичных представителей – определяются «расстояния» между ними. В результате принимается решение о принадлежности наблюдаемого процесса тому классу, для которого полученное «расстояние» минимально.
Для решения задачи классификации прежде всего необходимо выбрать модель анализируемых случайных процессов и метрику их сравнения.
8.2. Марковская модель случайного процесса
В качестве достаточно универсальной модели случайного квантованного по времени и уровню процесса  ,
,  - моменты квантования, наиболее целесообразно использовать простую цепь Маркова [1]. Марковский процесс
- моменты квантования, наиболее целесообразно использовать простую цепь Маркова [1]. Марковский процесс  может принимать одно из М возможных значений от
может принимать одно из М возможных значений от  до
до  , соответствующих уровням квантования
, соответствующих уровням квантования  . Значения
. Значения  меняются с ростом номера отсчета
меняются с ростом номера отсчета  , причем переход от одного
, причем переход от одного
состояния к другому является случайным и последующая величина  зависит только от предыдущей величины
зависит только от предыдущей величины  для всех
для всех  , как показано на рис. 8.1.
, как показано на рис. 8.1.
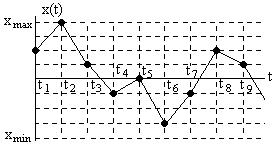
Рис. 8.1
Моделируемый процесс описывается квадратной матрицей переходных вероятностей 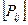 от значения
от значения 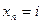 (номер строки) к значению
(номер строки) к значению 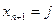 (номер столбца),
(номер столбца),
 =
= 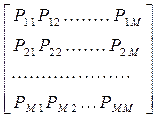 , (8.1)
, (8.1)
размера М´М, и матрицей-столбцом 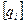 вероятностей начальных значений процесса
вероятностей начальных значений процесса 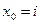 в момент времени
в момент времени  ,
,
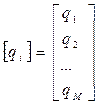 . (8.2)
. (8.2)
Для матрицы (8.1) для всех  выполняются условия
выполняются условия
 . (8.3)
. (8.3)
Классы сигналов проявляются в различных статистических свойствах наблюдаемого марковского процесса  и каждому из них должны соответствовать свои отличающиеся друг от друга матрицы
и каждому из них должны соответствовать свои отличающиеся друг от друга матрицы 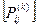 и
и 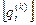 ,
, 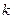 - номер класса. Они полностью определяют свойства анализируемых классов и фактически представляют собой «отпечатки» классифицируемых состояний.
- номер класса. Они полностью определяют свойства анализируемых классов и фактически представляют собой «отпечатки» классифицируемых состояний.
В качестве примера рассмотрим сигнал с четырьмя возможными значениями 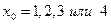 , матрица переходных вероятностей которого имеет вид
, матрица переходных вероятностей которого имеет вид
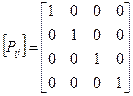 . (8.4)
. (8.4)
В этом случае при случайном выборе одного из начальных значений 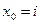 следующее значение может быть только тем же самым (с вероятностью 1). Таким образом матрица (8.3) порождает постоянный сигнал со случайным начальным значением.
следующее значение может быть только тем же самым (с вероятностью 1). Таким образом матрица (8.3) порождает постоянный сигнал со случайным начальным значением.
Для матрицы переходных вероятностей вида
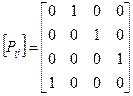 . (8.5)
. (8.5)
при случайном начальном значении 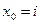 следующее значение детерминировано и равно
следующее значение детерминировано и равно 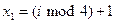 . При этом в дальнейшем сигнал представляет собой пилообразную функцию времени (получите этот результат самостоятельно, постройте графики). Пример программы расчета реализации сигнала показан на рис. 8.2.
. При этом в дальнейшем сигнал представляет собой пилообразную функцию времени (получите этот результат самостоятельно, постройте графики). Пример программы расчета реализации сигнала показан на рис. 8.2.
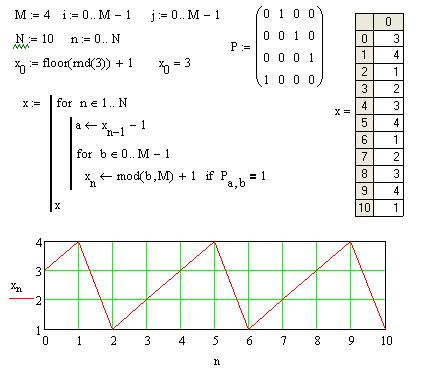
Рис. 8.2
На рис. 8.3 показана программа расчета реализации марковского случайного процесса при  . Как видно, в этом случае и форма сигнала становится случайной. Разработайте программы для произвольных значений числа
. Как видно, в этом случае и форма сигнала становится случайной. Разработайте программы для произвольных значений числа  градаций случайного процесса.
градаций случайного процесса.
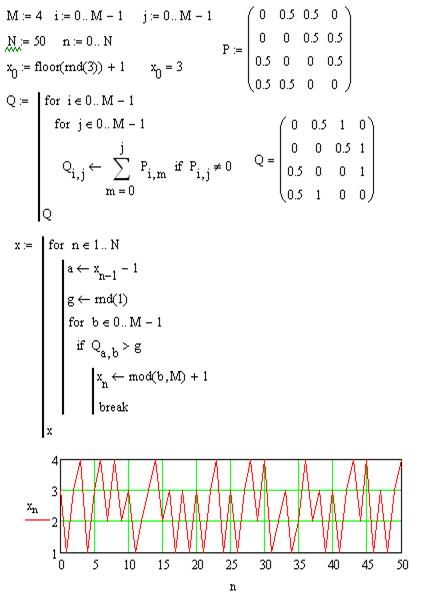
Рис. 8.3
8.3. Алгоритм классификации
Наблюдаемый марковский случайный процесс (сигнал)  может принадлежать одному из
может принадлежать одному из 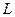 классов
классов 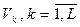 . В каждом k-ом классе дискретизированный процесс описывается матрицей переходных вероятностей вида
. В каждом k-ом классе дискретизированный процесс описывается матрицей переходных вероятностей вида
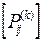 =
= 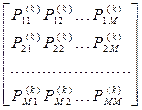 (8.6)
(8.6)
Пусть получена выборка значений 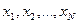 процесса
процесса  , содержащая
, содержащая  многоуровневых отсчетов. Тогда апостериорная вероятность принадлежности сигнала к классу
многоуровневых отсчетов. Тогда апостериорная вероятность принадлежности сигнала к классу 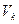 определяется выражением
определяется выражением
 , (8.7)
, (8.7)
где  - априорная вероятность появления сигнала из k-го класса,
- априорная вероятность появления сигнала из k-го класса, 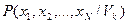 - вероятность появления заданной выборки отсчетов сигнала при условии его принадлежности классу
- вероятность появления заданной выборки отсчетов сигнала при условии его принадлежности классу 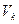 , а
, а 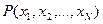 - безусловная вероятность выборки. Условная вероятность выборки
- безусловная вероятность выборки. Условная вероятность выборки 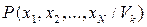 равна произведению вероятности
равна произведению вероятности  начальных значений
начальных значений 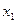 на вероятность перехода от
на вероятность перехода от 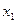 к
к 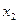 , затем на вероятность перехода от
, затем на вероятность перехода от 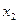 к
к 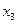 и так далее. Процесс умножения заканчивается
и так далее. Процесс умножения заканчивается
на вероятности перехода от  к
к 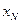 . Таким образом, получим (проделайте расчет самостоятельно)
. Таким образом, получим (проделайте расчет самостоятельно)
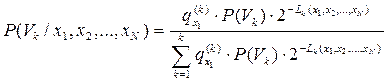 , (8.8)
, (8.8)
где
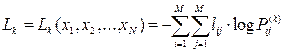 , (8.9)
, (8.9)
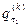 - вероятность начального значения
- вероятность начального значения  выборки в k-ом классе, через
выборки в k-ом классе, через 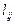 обозначено общее число переходов процесса из значения
обозначено общее число переходов процесса из значения  в значение
в значение 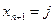 на следующем шаге для всех значений
на следующем шаге для всех значений 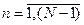 . Очевидно, что
. Очевидно, что
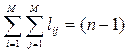 . (8.10)
. (8.10)
Как видно из (8.8), вероятность состояний определяется значениями 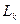 , k=1,...,L, которые в свою очередь зависят от выборки отсчетов случайного процесса. Величины
, k=1,...,L, которые в свою очередь зависят от выборки отсчетов случайного процесса. Величины 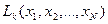 будем называть решающими статистиками, так как в них содержится вся необходимая для принятия решения информация о наблюдаемом процессе.
будем называть решающими статистиками, так как в них содержится вся необходимая для принятия решения информация о наблюдаемом процессе.
Процедура классификации заключается в следующем. Анализатор по поступающим выборочным отсчетам определяет числа 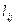 переходов процесса от одного значения к другому, которые накапливаются от начальных значений lij = 0 по мере появления новых отсчетов.
переходов процесса от одного значения к другому, которые накапливаются от начальных значений lij = 0 по мере появления новых отсчетов.
Затем вычисляются решающие статистики (8.9) для всех классов 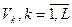 , выбирается минимальное значение
, выбирается минимальное значение 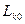 и минимальное из оставшихся значений
и минимальное из оставшихся значений 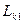 . Разность
. Разность  сравнивается с порогом
сравнивается с порогом
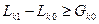 , (8.11)
, (8.11)
который определяется выражением
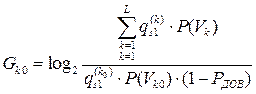 , (8.12)
, (8.12)
а при 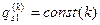 из (8.12) следует
из (8.12) следует
G = 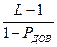 . (8.13)
. (8.13)
Доверительная вероятность 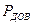 - это требуемый уровень условной вероятности выбранного класса для заданной выборки отсчетов сигнала. Она характеризует вероятность правильности принятого решения. Выражение (8.12) для порога с учетом (8.8) вытекает из равенства
- это требуемый уровень условной вероятности выбранного класса для заданной выборки отсчетов сигнала. Она характеризует вероятность правильности принятого решения. Выражение (8.12) для порога с учетом (8.8) вытекает из равенства
 . (8.14)
. (8.14)
Если неравенство (8.11) не выполняется, то принимается очередной отсчет и вновь вычисляются решающие статистики. Как только оно выполнится, анализ прекращается и выносится окончательное решение Vk0 с достоверностью не меньше Pдов.
Решающие статистики 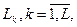 (8.9) определяют «расстояния» наблюдаемой реализации от соответствующих классов. Ее можно представить как точку в L-мерном гиперпространстве, координатами которой являются значения
(8.9) определяют «расстояния» наблюдаемой реализации от соответствующих классов. Ее можно представить как точку в L-мерном гиперпространстве, координатами которой являются значения 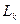 . На рис. 8.4 в качестве примера показаны области решающих статистик, соответствующие возможным различным решениям при L=2.
. На рис. 8.4 в качестве примера показаны области решающих статистик, соответствующие возможным различным решениям при L=2.
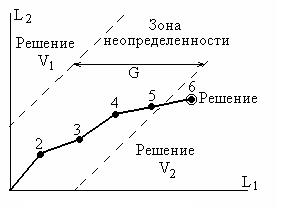
Рис. 8.4
Порог G определяет зону неопределенности (ограниченную пунктирными линиями на рис. 8.4), внутри которой решения не принимаются ввиду низкой достоверности. Левее расположена область, в которой принимается решение о принадлежности наблюдаемой реализации к первому классу, а правее – ко второму. Жирной линией показано движение точки, отображающей реализацию после поступления отсчетов с номерами 2, 3 и так далее (после шестого отсчета принимается решение 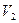 ).
).
В рамках предлагаемой методики классификации можно использовать сложные модели классов, определяемые несколькими марковскими моделями. В этом случае решающие
статистики целесообразно записать в виде двумерного массива 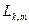 , где
, где 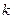 - номер класса, а
- номер класса, а 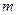 - номер модели внутри класса. Правило формирования решения предполагает определение минимального значения
- номер модели внутри класса. Правило формирования решения предполагает определение минимального значения 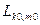 и следующего за ним
и следующего за ним 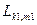 при
при 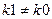 , а затем использование неравенства (8.11).
, а затем использование неравенства (8.11).
8.4. Обучение алгоритма классификации
Модели классов в виде матриц переходных вероятностей могут формироваться их теоретических (физических и математических) представлений о формировании классифицируемых сигналов. Достоверность классификации существенно зависит от точности используемых моделей.
На практике целесообразней использовать экспериментальные модели, полученные в результате обучения процедуры классификации. Обучение в технических системах может проводиться в режимах обучения с учителем и самообучения.
При обучении с учителем в систему классификации вводятся случайные сигналы с известными классами, по каторым формируются оценки матриц переходных вероятностей 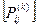 (8.1) и вероятностей начальных значений
(8.1) и вероятностей начальных значений 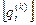 (8.2) для каждого из L классов. Для этого в реализациях
(8.2) для каждого из L классов. Для этого в реализациях 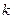 -ого класса определяется число переходов
-ого класса определяется число переходов 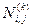 соседних отсчетов от i-ого значения к j-ому, тогда
соседних отсчетов от i-ого значения к j-ому, тогда
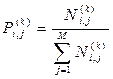 , (8.15)
, (8.15)
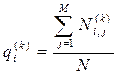 , (3.24)
, (3.24)
где  – общее число отсчетов. Матрицы
– общее число отсчетов. Матрицы 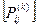 и
и 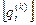 являются полным описанием (образом) k-ого класса. Возможно использование нескольких образов для описания классов сложной структуры в метрике решающей статистики.
являются полным описанием (образом) k-ого класса. Возможно использование нескольких образов для описания классов сложной структуры в метрике решающей статистики.
В режиме самообучения (обучения без учителя) используются неклассифицированные реализации случайных процессов. При этом согласно (8.15) и (8.16) оцениваются характеристики моделей для каждой реализации, и затем модели группируются по близости друг к другу в метрике решающей статистики (8.9). Проектирование системы классификации в режиме самообучения является достаточно сложной и неоднозначно решаемой задачей.
8.5. Результаты моделирования алгоритмов обучения
и классификации
Моделирование проведено с помощью пакета MathCAD 2001 для нормальных марковских процессов с различными дисперсиями 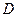 и коэффициентами корреляции
и коэффициентами корреляции 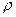 при заданных значениях объема обучающей реализации
при заданных значениях объема обучающей реализации 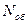 и доверительной вероятности
и доверительной вероятности 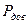 (напишите аналогичную программу самостоятельно). Число циклов моделирования выбиралось от 10000 до 50000.
(напишите аналогичную программу самостоятельно). Число циклов моделирования выбиралось от 10000 до 50000.
В программе формируются две обучающие реализации квазислучайных процессов с различными характеристиками длиной 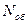 отсчетов, по которым в соответствии с (8.15), (8.16) определяются две марковские модели. Затем формируются
отсчетов, по которым в соответствии с (8.15), (8.16) определяются две марковские модели. Затем формируются 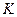 реализаций одного из процессов, и в соответствии с разработанной процедурой определяется их принадлежность к каждому из классов. После этого моделирование циклически повторяется для набора статистического материала.
реализаций одного из процессов, и в соответствии с разработанной процедурой определяется их принадлежность к каждому из классов. После этого моделирование циклически повторяется для набора статистического материала.
На рис. 8.5 показаны зависимости вероятности ошибки от объема обучающей выборки 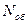 при классификации про-
при классификации про-
цессов по дисперсии для двух классов, первый характеризуется дисперсией 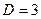 и коэффициентом корреляции
и коэффициентом корреляции 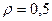 , а второй -
, а второй - 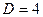 и
и 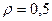 . На рис. 8.6 представлены величины среднего числа отсчетов
. На рис. 8.6 представлены величины среднего числа отсчетов  , необходимых для принятия решения с требуемой достоверностью.
, необходимых для принятия решения с требуемой достоверностью.
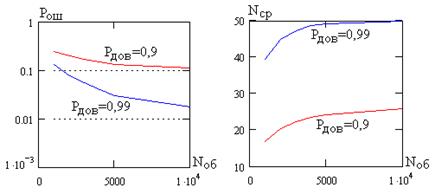
Рис. 8.5. Рис. 8.6
Как видно, при небольшом объеме обучающей выборки вероятность ошибки весьма высока (алгоритм «плохо обучен»). При накоплении информации о разделяемых классах она стремится к заданной величине 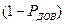 . Для обеспечения большей достоверности результата необходимо увеличивать
. Для обеспечения большей достоверности результата необходимо увеличивать 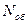 . Среднее число отсчетов сравнительно невелико, то есть алгоритм классификации работает достаточно быстро.
. Среднее число отсчетов сравнительно невелико, то есть алгоритм классификации работает достаточно быстро.
На рис. 8.7 представлена зависимость вероятности ошибки от объема обучающей выборки при классификации по коэффициенту корреляции. Первый класс имеет 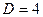 и
и 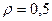 , а второй -
, а второй - 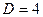 и
и  . На рис. 8.8 показаны аналогичные зависимости при различении близких классов по дисперсии, первый характеризуется
. На рис. 8.8 показаны аналогичные зависимости при различении близких классов по дисперсии, первый характеризуется 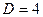 и
и 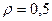 , а второй -
, а второй - 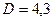 и
и 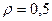 .
.
Рис. 8.7 Рис. 8.8
Результаты моделирования свидетельствуют, что процедура классификации уверенно определяет принадлежность наблюдаемой реализации к соответствующему семейству при различных условиях определения различий классов (параметрическое описание сигналов просто не требуется). Чем ближе друг к другу свойства классов, тем больший объем обучающей выборки необходим для их различения с заданной достоверностью.
8.6. Классификационная скрытность сигналов
Для выявления принадлежности случайного сигнала одному из выбранных классов с заданной достоверностью  необходимо затратить определенное среднее число
необходимо затратить определенное среднее число  отсчетов.
отсчетов.
Классификационная скрытность оценивается величиной  или длительностью реализации в единицах времени. Так как алгоритм классификации оптимален по критерию максимальной апостериорной вероятности, то при его использовании определяется потенциальная скрытность случайного сигнала.
или длительностью реализации в единицах времени. Так как алгоритм классификации оптимален по критерию максимальной апостериорной вероятности, то при его использовании определяется потенциальная скрытность случайного сигнала.
Классификационная скрытность повышается с ростом требуемой достоверности и при сближении статистических характеристик классов. Существенное влияние на характеристики алгоритма классификации оказывает процедура обучения и, в частности, продолжительность обучающих выборок. При обучении с учителем необходимо обеспечивать достоверную принадлежность обучающих выборок соответствующему классу.
8.7. Применение алгоритмов классификации
случайных процессов
Задача классификации случайных процессов возникает в самых различных областях человеческой деятельности.
В медицинской диагностике широко используются решении и принадлежности наблюдаемых процессов (кардиограмм, энцефалограмм и т.д.) соответствующему классу - состоянию пациента (норма, заболевание первой или второй степени, тяжелое состояние).
В технике необходимо по сигналам датчиков контролировать состояние устройства (авиационного или автомобильного двигателя, турбины на электростанции), в том числе и с целью прогнозирования возможной неисправности (классами могут быть состояния угрозы неисправности).
В военной технике необходимо определять тип выявляемого объекта (автомобиль, танк, колонна солдат, или тип пролетающего самолета) по наблюдаемым акустическим или электромагнитным случайным сигналам.
ЗАЩИЩЕННОСТЬ РАДИОЛИНИЙ
9.1. Основные понятия
Одной из важнейших характеристик системы связи является ее способность противостоять целенаправленному противодействию потенциального противника. Исследования в этом направлении проводятся практически непрерывно с момента возникновения систем радиосвязи.
Системы связи специального назначения должны функционировать в условиях радиопротиводействия со стороны противника. Его действия могут преследовать различные цели:
n обнаружение факта работы системы;
n определение параметров радиопередачи (частоты и др.);
n определение местоположения радиостанции;
n перехват информации;
n подавление радиосвязи преднамеренными помехами;
n уничтожение источника излучения.
Система связи должна иметь возможность препятствовать или затруднять противнику достижение его целей. Для этого она должна обеспечить максимальную неопределенность (неосведомленность) противника относительно интересующих его параметров передачи.
Если параметры неизменны в процессе функционирования, то неосведомленность противника обеспечивается их секретностью. Секретность - система мер, направленных на то, чтобы противник не получил необходимую информацию. Это организационные меры: охрана, ограничение доступа к информации, специальные режимы работы (радиомолчание) и др. Пример - шифрование передаваемой информации. Простые шифры - просто раскрываются. Сложные шифры - могут быть переданы противнику (пример - шифр командования сухопутных войск Германии во второй мировой войне). Секретность - ненадежный способ борьбы с радиопротиводействием.
Более эффективно обеспечивать неосведомленность противника за счет случайной (для него) оперативной смены рабочих параметров радиопередачи в процессе функционирования системы связи.
Противник располагает сведениями о совокупности возможных параметров системы связи (например, о множестве рабочих частот), но не знает их значений в текущем сеансе связи. Он вынужден определять их по принимаемым сигналам, а для этого необходимы аппаратные и временные затраты.
Скрытность - мера временных и аппаратных затрат противника для обнаружения и определения сменных параметров радиопередачи. Программа смены рабочих параметров должна быть случайной для противника и при необходимости защищаться мерами секретности.
Чем выше неопределенность противника о рабочих параметрах радиопередачи, тем выше необходимые энергетические затраты для ее подавления. Ресурсы постановщика помех всегда ограничены, имеют высокую стоимость. Источник помех может быть обнаружен и уничтожен, что также повышает затраты противника.
Защищенность - мера затрат противника (энергетических и аппаратных ресурсов, боеприпасов и др.) для решения задачи противодействия. Если рассматривается задача радиоподавления системы связи, то защищенность характеризуется необходимой суммарной мощностью создаваемых противником помех.
9.2. Защищенность и скрытность
Система радиосвязи функционирует в условиях естественных (шумовых, внутрисистемных, взаимных) помех и противодействия противника.
Естественные помехи учитываются на этапах проектирования и эксплуатации системы выбором технических средств, обеспечивающих требуемое качество связи.
Противодействие предполагает активное, целенаправленное воздействие противника на систему радиосвязи путем создания преднамеренных помех или, например, физического уничтожения элементов системы.
Активное "контрнаступление" на противника не входит в задачи системы радиосвязи. Ей отводится пассивная роль защиты от действий противника, заключающейся в создании условий, в которых противник будет вынужден затрачивать больше ресурсов и времени на решение поставленной ему задачи. Эта сторона деятельности системы характеризуется ее защищенностью -многоплановым понятием, структура которого приведена на рис. 9.1.

Рис. 9.1
Защищенность системы радиосвязи от воздействия со стороны противника включает в себя защищенность от радиоэлектронного подавления (РЭП) и защищенность от других воздействий, ведущих к физическому уничтожению ее элементов.
Для противодействия работе системы радиосвязи противник использует источники помех, которые либо затрудняют передачу сообщений, либо полностью подавляют радиоканал, исключая возможность передачи информации.
В первом случае свойства системы связи характеризуются помехозащищенностью - вероятностью  своевременной доставки сообщений в условиях РЭП за время,
своевременной доставки сообщений в условиях РЭП за время,
не большее заданной величины  . Это характеристика качества связи и мера мешающего действия противника, при котором система радиосвязи еще способна выполнять свои функции ценой допустимых затрат времени
. Это характеристика качества связи и мера мешающего действия противника, при котором система радиосвязи еще способна выполнять свои функции ценой допустимых затрат времени 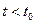 .
.
Всегда можно указать такой уровень организованных помех в определенном диапазоне частот, при котором работа системы радиосвязи будет полностью подавлена. В этой ситуации характеристикой защищенности является минимальная суммарная средняя мощность 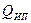 источника помех в заданном диапазоне частот на определенном удалении от системы связи, при которой величина вероятности доставки
источника помех в заданном диапазоне частот на определенном удалении от системы связи, при которой величина вероятности доставки 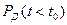 становится ниже допустимой. Величина
становится ниже допустимой. Величина 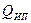 определяется свойствами радиостанций (сигналами, способами их обработки и пр.), действиями системы по уклонению от подавления (например, за счет смены рабочих частот) и характеристиками источника помех (его удалением, полосой частот, прицельностью помехи). При прочих равных условиях, чем больше требуемая мощность передатчика помех, тем выше защищенность системы связи от РЭП. Величина
определяется свойствами радиостанций (сигналами, способами их обработки и пр.), действиями системы по уклонению от подавления (например, за счет смены рабочих частот) и характеристиками источника помех (его удалением, полосой частот, прицельностью помехи). При прочих равных условиях, чем больше требуемая мощность передатчика помех, тем выше защищенность системы связи от РЭП. Величина 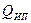 является характеристикой затрат ресурсов противника, необходимых для подавления системы радиосвязи. Очевидно, что абсолютное значение мощности источника помех неудобно в качестве меры защищенности в силу зависимости от большого числа параметров. Лучших результатов можно ожидать при использовании нормированных энергетических характеристик.
является характеристикой затрат ресурсов противника, необходимых для подавления системы радиосвязи. Очевидно, что абсолютное значение мощности источника помех неудобно в качестве меры защищенности в силу зависимости от большого числа параметров. Лучших результатов можно ожидать при использовании нормированных энергетических характеристик.
Эффективность подавления зависит от степени информированности противника о свойствах системы, то есть защищенность от РЭП (и от других воздействий) тесно связана с разведывательной защищенностью (скрытностью). По мере поступления дополнительных сведений (о сигналах, их частотах, параметрах структуры) противник получает возможность точнее "прицелиться" и снизить суммарные затраты мощности
источника помех или перейти от мешающего действия к полному подавлению системы связи.
Защищенность от других воздействий целесообразно оценивать вероятностью поражения  элементов системы радиосвязи. Современные системы включают в себя сотни радиостанций, а противник располагает ограниченными ресурсами и временем. Поэтому неизбежна необходимость избирательного поражения вполне определенных узловых элементов (центральной, реперных станций, узлов ретрансляции). В этом случае повышается роль разведзащищенности, тем более, что время изменения местоположения станций системы радиосвязи много больше времени смены параметров излучаемых сигналов.
элементов системы радиосвязи. Современные системы включают в себя сотни радиостанций, а противник располагает ограниченными ресурсами и временем. Поэтому неизбежна необходимость избирательного поражения вполне определенных узловых элементов (центральной, реперных станций, узлов ретрансляции). В этом случае повышается роль разведзащищенности, тем более, что время изменения местоположения станций системы радиосвязи много больше времени смены параметров излучаемых сигналов.
Смысл вероятности поражения зависит от ее величины. Если  близка к единице, то это мера успеха противника при однократном воздействии. При малой вероятности поражения (например, меньше 0,5) противник вынужден повторять попытки воздействия для повышения общей вероятности успеха, которая должна быть больше
близка к единице, то это мера успеха противника при однократном воздействии. При малой вероятности поражения (например, меньше 0,5) противник вынужден повторять попытки воздействия для повышения общей вероятности успеха, которая должна быть больше  . При независимых событиях вероятность успешного поражения за
. При независимых событиях вероятность успешного поражения за  попыток равна
попыток равна


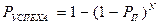 , (9.1)
, (9.1)
а среднее число попыток поражения  определяется равенством
определяется равенством
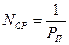 . (9.2)
. (9.2)
В этом случае  (обратная ей величина) характеризует затраты средств уничтожения. При эксплуатации системы радиосвязи необходимо обеспечивать снижение вероятности поражения ее узловых элементов, используя, например, их имитаторы.
(обратная ей величина) характеризует затраты средств уничтожения. При эксплуатации системы радиосвязи необходимо обеспечивать снижение вероятности поражения ее узловых элементов, используя, например, их имитаторы.
Таким образом, защищенность от воздействий системы радиосвязи можно определять тремя характеристиками :
- вероятностью 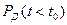 доставки сообщений за время
доставки сообщений за время  , не превышающее заданную величину
, не превышающее заданную величину  , при достаточно слабых воздействиях, когда сохраняется работоспособность системы;
, при достаточно слабых воздействиях, когда сохраняется работоспособность системы;
- нормированной суммарной мощностью источника помех при условии подавления системы (сильное воздействие);
- вероятностью поражения  , если противник решает задачу уничтожения.
, если противник решает задачу уничтожения.
Разведывательная защищенность (скрытность) системы радиосвязи рассматривается, как ее способность противостоять выявлению противником ее рабочего состояния (факта функционирования, сигналов, местоположения, структуры, передаваемой информации), что отражает диаграмма, приведенная на рис. 9.2.
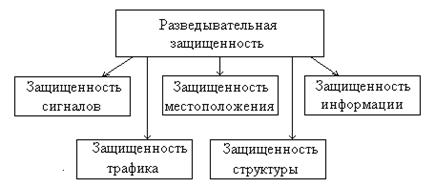 Рис. 9.2
Рис. 9.2
Целесообразно полагать, что противник всегда может с заданной достоверностью установить необходимый объем сведений о системе ценой соответствующих затрат времени и ресурсов. Важнейшей задачей противника является минимизация этих затрат. Тогда наиболее рациональной оказывается такая
мера разведзащищенности, как минимальное среднее время, необходимое для выявления с заданной достоверностью состояния системы радиосвязи одним оптимальным анализатором. Это определение полностью соответствует мере скрытности, введенной в [1] для произвольных событий.
Таким образом, разведзащищенность системы радиосвязи может оцениваться ее скрытностью и выражаться в двоичных измерениях (диз'ах) [1] или единицах времени.
9.3 Мера защищенности от подавления
Для радиоэлектронного подавления системы радиосвязи противник использует источник (передатчик) помех. Эффективность подавления определяется мощностью помехи в точке приема и ее оптимальностью - близостью к свойствам информационных сигналов.
Целесообразно пользоваться нормированной величиной - отношением  мощности помехи
мощности помехи 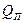 к мощности сигнала
к мощности сигнала 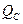 в точке приема,
в точке приема,
 (9.3)
(9.3)
Введем в рассмотрение идеальный постановщик помех (ИПП), располагающий всей информацией о подавляемой системе связи (о сигналах, синхронизации, местоположении и т.д.). Он характеризуется минимальной мощностью 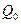 оптимальной помехи в точке приема, достаточной для подавления системы.
оптимальной помехи в точке приема, достаточной для подавления системы.
Характеристики качества системы радиосвязи (например, вероятность доставки сообщения) зависят от уровня и свойств помехи в точке приема. Для оценки защищенности необходимо установить обратную зависимость мощности помехи от характеристик системы.
В сложной системе связи можно выделить наиболее уязвимые подсистемы (синхронизации, передачи команд управления и другие). При этом защищенность системы в целом определяется свойствами отдельные ее компонент и зависит от текущего режима функционирования.
В наиболее простом случае в качестве основных характеристик системы связи можно рассматривать вероятность ошибки 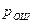 передачи дискретного символа. Она достаточно хорошо изучена для различных методов обработки сигналов и видов помех. Из имеющихся соотношений можно определить зависимость защищенности
передачи дискретного символа. Она достаточно хорошо изучена для различных методов обработки сигналов и видов помех. Из имеющихся соотношений можно определить зависимость защищенности  от допустимой вероятности ошибки
от допустимой вероятности ошибки 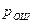 . Задача существенно усложняется при введении кодирования сообщений и учете свойств реальных каналов связи.
. Задача существенно усложняется при введении кодирования сообщений и учете свойств реальных каналов связи.
Применительно к двоичному каналу с частотным телеграфированием (ЧТ) и некогерентным приемом вероятность ошибки в условиях действия оптимальной помехи и при бесконечном отношении сигнал/шум 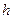 приближенно равна [6-8]
приближенно равна [6-8]
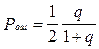 , (9.4)
, (9.4)
тогда получим
 . (9.5)
. (9.5)
Зависимость  от
от 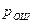 показана на рис. 9.3. Как видно, при малой допустимой вероятности ошибки защищенность мала, при
показана на рис. 9.3. Как видно, при малой допустимой вероятности ошибки защищенность мала, при 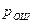 = 0,25 получим
= 0,25 получим 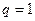 , что вполне соответствует подавлению канала связи при отсутствии кодирования, а при
, что вполне соответствует подавлению канала связи при отсутствии кодирования, а при 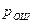 ®0,5 (используется мощная система помехоустойчивого кодирования) защищенность стремится к бесконечности.
®0,5 (используется мощная система помехоустойчивого кодирования) защищенность стремится к бесконечности.
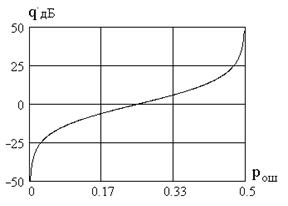
Рис. 9.3
9.4. Собственная защищенность
Введем величину собственной защищенности системы радиосвязи 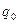 , равной
, равной
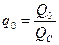 . (9.6)
. (9.6)
Она является характеристикой системы, предполагает воздействие идеального постановщика помех и не зависит от действий противника.
С помощью 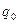 можно оценивать эффективность технических решений, принимаемых в системе для повышения ее защищенности от помех. Например, если в системе передачи дискретных сообщений при отсутствии специальных мер по защите информации ее работоспособность нарушается при
можно оценивать эффективность технических решений, принимаемых в системе для повышения ее защищенности от помех. Например, если в системе передачи дискретных сообщений при отсутствии специальных мер по защите информации ее работоспособность нарушается при 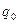 =0,01 (-20 дБ), а при использовании помехоустойчивого кодирования уровень собственной защищенности повышается до
=0,01 (-20 дБ), а при использовании помехоустойчивого кодирования уровень собственной защищенности повышается до 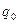 =0,1 (-10 дБ), то выигрыш составляет 10 дБ.
=0,1 (-10 дБ), то выигрыш составляет 10 дБ.
Следует ожидать, что собственная защищенность системы связи всегда будет сравнительно невелика ( 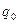 меньше единицы). Это относится и к системам с широкополосными сигналами, и к ППРЧ, так как идеальный постановщик помех располагает всей информацией о передаваемых сигналах. Эффективность различных методов защиты обусловлена лишь практической невозможностью реализации идеального постановщика помех.
меньше единицы). Это относится и к системам с широкополосными сигналами, и к ППРЧ, так как идеальный постановщик помех располагает всей информацией о передаваемых сигналах. Эффективность различных методов защиты обусловлена лишь практической невозможностью реализации идеального постановщика помех.
9.5. Мера защищенности
Как уже отмечалось, характеристикой затрат противника по подавлению системы радиосвязи является минимальная суммарная средняя мощность 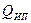 источника помех на определенном удалении от системы связи, при которой величина вероятности доставки
источника помех на определенном удалении от системы связи, при которой величина вероятности доставки 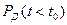 становится ниже допустимой. Мощность помех
становится ниже допустимой. Мощность помех 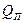 , создаваемая этим источником в точке приема, а точнее, ее относительный уровень q, характеризует защищенность системы. Связь между
, создаваемая этим источником в точке приема, а точнее, ее относительный уровень q, характеризует защищенность системы. Связь между 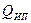 и
и 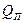 определяется характеристиками постановщика помех и трассы их распространения.
определяется характеристиками постановщика помех и трассы их распространения.
Неоптимальный характер помехи может быть обусловлен следующими причинами:
- требуемая точность установки параметров помехи (например, ее синхронность с принимаемым информационным сигналом) не реализуется на практике;
- противник не располагает всей необходимой априорной информацией о сменных параметрах сигналов системы радиосвязи и получает ее как результат текущей разведки при соответствующих временных затратах.
Первая из них может возникать в системах связи с ШПС, а вторая - при использовании ППРЧ.
Таким образом, в качествемеры защищенности от РЭП будем использовать норм
