Ранговый алгоритм обнаружения

СИГНАЛОВ С ППРЧ

7.1. Алгоритм обнаружения

Рассмотренный ранговый алгоритм многоканального обнаружения может быть использован для выявления наличия сигналов с ППРЧ, о чем может свидетельствовать снижение среднего значения ранга в том из каналов, в котором в данный момент времени присутствует сигнал. Накапливая уменьшающиеся средние ранги в каналах, по которым перестраивается передатчик, можно осуществить энергетическое обнаружение сигнала с ППРЧ в целом.

Пусть узкополосный радиосигнал (его энергетический спектр 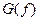показан на рис. 7.1) с шириной спектра Df₀ перестраивается по M каналам с несущими частотами 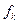, , 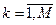оставаясь в каждом из них в течение N₀ отсчетов длительностью t₀=1/Df₀.

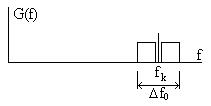
Рис. 7.1

В качестве иллюстрирующего примера допустим, что в каждом из каналов действует гауссовская помеха с дисперсией s_ш² и может присутствовать гауссовский случайный сигнал с общей для сигнала и помехи дисперсией s_с², равной

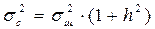. (7.1)

На рис.7.2 показаны временные реализации процессов

в каналах с номерами k₁ и k₂ при M=5, N₀=50, s_ш² =1 и h=3 (s_с² =10), t - дискретное время в числе интервалов квантования.

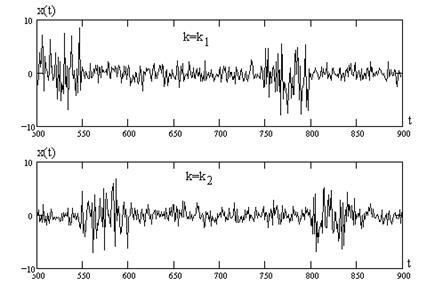
Рис. 7.2

На рис. 7.3 показана зависимость мгновенных значений ранга в канале j=k₁ (первый график на рис. 7.2).

Как видно, в целом имеет место снижение ранга в моменты появления сигнала (t=500-550 и t=750-800), но для его выявления необходимо усреднение рангов на интервале N₁ отсчетов. На рис. 7.4 показаны примеры такого усреднения при N₁=5 и N₁=30 соответственно для рангов на рис. 7.3.

Из приведенных зависимостей следует, что необходимо усреднение рангов при N₁ не менее нескольких десятков. С уменьшением отношения сигнал/помеха величина N₁ должна увеличиваться.

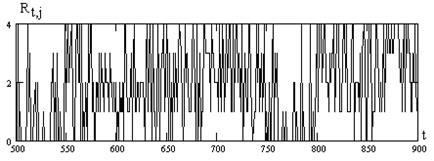Рис. 7.3

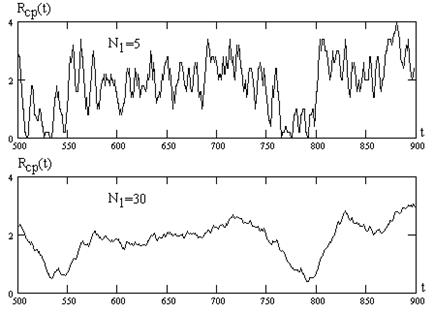
Рис. 7.4

На рис. 7.5 условно показаны сигналы 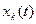и соответствующие им средние ранги 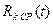для двух каналов. Допустим, что алгоритм обнаружения выделяет участки пониженного среднего ранга и формирует общий, объединенный по всем каналам общий ранг 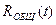, показанный на нижнем графике

рис. 7.5. Решения принимаются по выборке объема 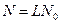, кратного продолжительности занятия одного канала N₀.

Проведем анализ в терминах нормированных рангов. Усредненные ранги имеют нормальное распределение вероятностей. При отсутствии сигнала среднее значение нормированного ранга 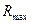равно (6.41)

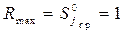, (7.2)

а при его наличии минимальная величина ранга 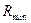определяется (6.42),

. (7.3)

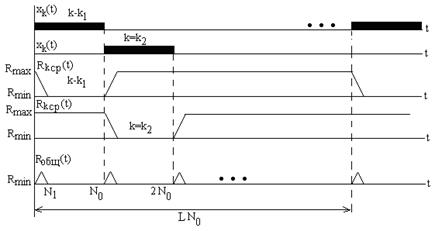
Рис. 7.5

Задачей обнаружителя является выявление каналов, в которых в данный момент времени наблюдается снижение среднего ранга, что свидетельствует о наличии сигнала. Возможны различные варианты решения этой задачи.

Оптимальный алгоритм должен формировать реализацию минимальных средних рангов, как показано на последнем графике рис. 7.5, соответствующем случаю N₀ > N₁ (медленная ППРЧ). В области 2N₀ > N₁ > N₀ возникает вариант, показанный на рис. 7.6. Как видно, оптимальный алгоритм предполагает идеальное выделение минимального среднего ранга, а значит будет обеспечивать наименьшее время обнаружения (его нижнюю оценку).

Рис. 7.6

Определим общее по всем каналам среднее значение ранга для рассмотренного оптимального алгоритма при наличии сигнала в соответствии с нижним графиком рис. 7.5 и рис. 7.6. Отмеченные на рис. 7.6 величины a и b равны

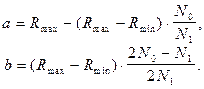(7.4)

Нетрудно показать, что

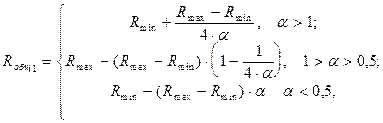(7.5)

где введено обозначение

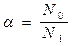, (7.6)

величина a представляет собой нормированную продолжительность занятия канала элементом сигнала с ППРЧ.

На рис. 7.7 показаны зависимости от отношения сигнал/шум h (в децибелах) величин R_max и R_min согласно (7.2) и (7.3), а на рис. 7.8 приведена зависимость (7.5) усредненного ранга R_{общ 1} от a для рассматриваемого идеального алгоритма и нормального распределения сигнала и помехи.

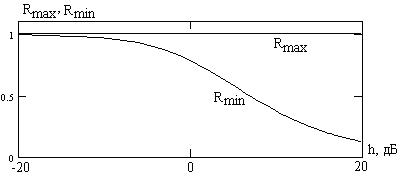
Рис. 7.7

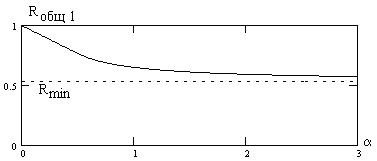
Рис. 7.8

Как видно из рис. 7.8, уменьшение продолжительности занятия одного канала 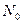по отношению к величине интервала предварительного накопления рангов 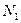(увеличение скорости ППРЧ) приводит к росту среднего ранга при наличии сигнала. Это обусловлено тем, что в интервал усреднения 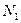в канале с сигналом могут попадать значения рангов при отсутствии сигнала (он еще не появился или передатчик переключился на другой канал внутри интервала 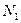) и количество таких мешающих отсчетов ранга повышается с уменьшением .

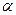Снижение влияния сигнальной компоненты в ранговой статистике можно отразить эквивалентным уменьшением отношения сигнал/помеха 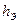. Для этого необходимо при заданных 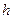и a определить 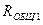и из (7.5) найти такое значение 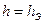, при котором 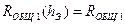. На рис. 7.9 показана зависимость 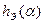при исходном отношении сигнал/помеха .

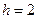Проведенный анализ свидетельствует о существенном снижении эквивалентного отношения сигнал/помеха 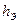в области a<0,5 (при a=0,5 получим 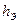=1,05 или в два раза меньше исходного).

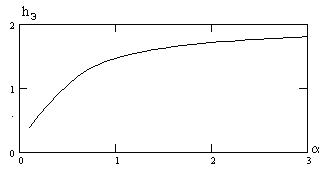
Рис. 7.9

Таким образом повышение скорости перестройки сигналов с ППРЧ (уменьшение 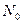) приводит к снижению эквивалентной помехоустойчивости разведывательного приемника.

Дисперсии рангов, усредненных по отрезкам из 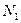отсчетов, согласно (6.44) приближенно равны

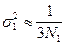, (7.7)

тогда дисперсия решающей статистики (среднего ранга по всей выборке объема N) определяется выражением

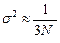. (7.8)

На рис. 7.10 приведена зависимость необходимых временных затрат N (энергетической скрытности сигнала с ППРЧ) от величины a (нормированного времени занятия одного канала) при 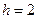(6 дБ), вероятности ошибок P=10^-3 и P=10^-1, 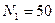и числе каналов M=256.

Как видно, временные затраты на обнаружение резко нарастают в области a < 1, при a = 0,1 величина N возрастает

на два порядка по сравнению с большими значениями a, при которых сигнал с ППРЧ соответствует узкополосному.

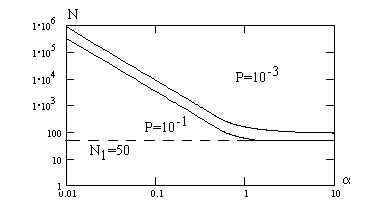
Рис. 7.10

Полученные для идеального алгоритма зависимости вида рис. 7.10 представляют нижнюю оценку необходимого числа отсчетов N.

Рассмотрим реальный и явно не высокоэффективный алгоритм принятия решения о наличии сигнала с ППРЧ. В каждом из каналов формируются усредненные в течение N₁ отсчетов значения нормированного к (6.40) среднего ранга R_i и вычисляется их произведение

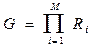(7.9)

Последовательные значения статистики G (7.9) накапливаются в течение N отсчетов (N кратно N₁) и сравниваются с порогом. Если полученная усредненная величина G_ср меньше заданного уровня, принимается решение о наличии сигнала с ППРЧ.

Статистику G можно приближенно представить в виде

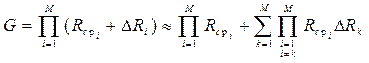(7.10)

где R_{ср i} - среднее значение ранга, равное единице при отсутствии сигнала в i-м канале и определяемое (7.3) при наличии сигнала, а DR_i - малое случайное отклонение ранга, DR_i << R_{ср i} , что имеет место при N₁>>1. Из (7.10) приближенно получим

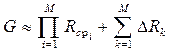. (7.11)

Ранговая статистика G является приближенно нормальной случайной величиной со средним значением, равным единице при отсутствии сигнала и R_{общ 1} из (7.5) при его наличии с дисперсией 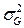, в M раз большей дисперсии ранговой статистики (7.8) для идеального алгоритма принятия решения,

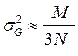. (7.12)

Таким образом, необходимый объем выборки N для рассматриваемого алгоритма обнаружения в M раз больше, чем для идеального. Полученные значения являются верхней оценкой энергетической скрытности сигналов с ППРЧ, выраженной в числе отсчетов.

7.2. Скрытность сигналов с ППРЧ

Энергетическая скрытность сигналов с ППРЧ, выраженная в числе N отсчетов определяется по описанной выше методике и характеризуется зависимостями вида рис. 7.10.

В абсолютных временных единицах энергетическая скрытность равна времени обнаружения сигнала с заданной достоверностью и определяется выражением

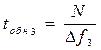, (7.13)

где 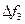- полоса частот узкополосного канала сигнала с ППРЧ. На рис. 7.11 показана зависимость времени обнаружения сигнала с ППРЧ от нормированной длительности элемента a для идеального алгоритма принятия решения при h=2, вероятности ошибок P=10^-3, N₁ = 50, числе каналов M=256 и Df₃=19,5 кГц.

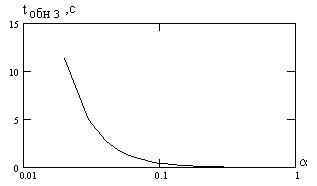
Рис. 7.11

Как видно, при a<0,1 (быстрая ППРЧ) энергетическая скрытность рассматриваемых сигналов резко нарастает.

Таким образом, энергетическая скрытность сигналов с ППРЧ существенно зависит от отношения сигнал/шум и скорости смены частот. Медленная ППРЧ при a>1 (в рассматриваемом примере менее 200 скачков в секунду) имеет крайне низкую энергетическую скрытность, близкую к скрытности узкополосных сигналов. При малых a энергетическая скрыт-

ность резко повышается, достигая максимума для поэлементной ППРЧ.

7.3. Сравнительный анализ энергетической скрытности

сигналов

Пусть ШПС занимает полосу частот сигнала с ППРЧ, тогда

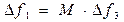, (7.14)

где Df₁ и Df₃ - полосы частот ШПС и узкополосного канала, а M - число частотных каналов в сигнале с ППРЧ. При одинаковой энергетике отношения сигнал/шум h₁² в широкополосном канале и h₃² для сигнала с ППРЧ связаны соотношением

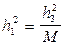. (7.15)

Тогда можно определить числа отсчетов N₁ и N₃ , необходимых для обнаружения ШПС и сигналов с ППРЧ соответственно.

В качестве примера рассмотрим ШПС с Df₁ = 5 МГц, 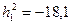дБ при оптимальном параметрическом обнаружении и сигнал с ППРЧ с M = 256, Df₃ = 19,5 кГц, h₁² = 6,021 дБ (h₁²=2) при ранговом алгоритме обнаружения. Тогда получим N₁ = 3,176 10⁵ (рис. 3.1) при ШПС и N₃ = 2,207 10⁵ (рис. 7.10) при поэлементной ППРЧ (N₀ = 1, a = 0,05). Как видно, в этом случае необходимое число измерений примерно одинаково.

Время обнаружения анализируемых сигналов определяется из (3.9) и (7.13), тогда в рассматриваемом примере получим

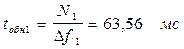(7.16)

для ШПС и

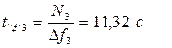(7.17)

для сигналов с ППРЧ.

Как видно, время обнаружения сигналов с поэлементной ППРЧ - энергетическая скрытность в единицах времени - значительно (в 178 раз) больше, чем ШПС. Это обусловлено тем, что при ППРЧ отсчеты сигнала формируются в узкополосном канале с частотой в M раз меньшей, чем для ШПС.

При снижении скорости смены частоты в четыре раза (a = 0,08, N₀ = 4) необходимое число отсчетов N₃ резко падает и энергетические скрытности сигналов с ППРЧ и ШПС становятся примерно одинаковыми.

Энергетическая скрытность резко возрастает с уменьшением отношения сигнал/шум h². Затраты на обнаружение противником узкополосных сигналов при h²>1 сравнительно невелики. Для ШПС при h²<<1 оптимальное параметрическое обнаружение практически нереализуемо из-за высоких требований к точности оценки мощности шума в канале разведывательного приемника.

Широкополосные сигналы с большой базой обладают высокой энергетической скрытностью и практически не обнаруживаются энергетическим приемником. Для их выявления необходимо использовать корреляционную обработку и соответствующую поисковую процедуру в множестве рабочих структур.

Энергетическая скрытность сигналов с медленной ППРЧ невелика и близка к скрытности узкополосных сигналов. Высокая энергетическая скрытность обеспечивается при длительности занятия частотного канала, меньшей продолжительности нескольких независимых отсчетов, то есть при использовании высокоскоростной ППРЧ. Наилучшие результаты имеют место для сигналов с поэлементной ППРЧ, энергетическая скрытность которых выше скрытности ШПС.