Классификация состояний цепи Маркова.

Пусть - простая цепь Маркова с состояниями А₁, А₂,…

Определение: Состояние А_i называется не существенным, если существует такое состояние А_j что для некоторого K_{0 ,} но _. В противном случае состояние А_i называется существенным.

Не существенное – если найдется А_j , такое что попав туда мы не сможем вернутся.

Определение: Два существенных состояния А_i и А_j называется сообщающимися если K и m, такие что и _. Иначе состояния не сообщающиеся.

А₁ и А₂ не существенные, А₃ и А₄ существенные и сообщающиеся.

Теорема солидарности.

Цепь называется неприводимой, если все состояния ее образуют единственный класс либо невозвратных, либо возвратных состояний.

Теорема солидарности.

В неприводимой цепи все состояния принадлежат одному типу: если хоть одно возвратно, то все возвратные, если хоть одно нулевое, то все нулевые, если хоть одно периодично, то все периодичны.

35.

Теорема о предельных вероятностях.

Если при некотором t₀ все элементы матрицы P^t =[u_ij^(t)] положительны, то существуют пределы

где j = 1, …, r. Предельные вероятности b_j не зависят от начального состояния E_i и являются единственным решением системы уравнений

где j=1, 2, ..., r.

Физический смысл этой теоремы заключается в том, что вероятности нахождения системы в состоянии E_j практически не зависит от того, в каком состоянии она находилась в далеком прошлом.

36.

Случайные процессы.

Случайный процесс (случайная функция) — семейство случайных величин, индексированных некоторым параметром, чаще всего играющим роль времени или координаты.

Пусть дано вероятностное пространство 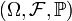. Параметризованное семейство 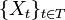случайных величин

,

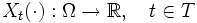где T произвольное множество, называется случайной функцией.

Если 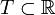, то параметр 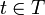может интерпретироваться как время. Тогда случайная функция {X_t} называется случайным процессом. Если множество T дискретно, например 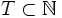, то такой случайный процесс называется случайной последовательностью.

Марковские процессы со счетным множеством состояний.

Марковский процесс — случайный процесс, эволюция которого после любого заданного значения временного параметра t не зависит от эволюции, предшествовавшей t, при условии, что значение процесса в этот момент фиксировано («будущее» процесса не зависит от «прошлого» при известном «настоящем»).

В марковских процессах со счетным множеством состояний – количество состояний ограничено, а переходы могут осуществляться как дискретно в определенные моменты времени t₁, t₂, … или в момент времени t.

Случайный процесс называется процессом с дискретными состояниями, если возможные состояния системы S₁, S₂,S₃…можно перечислить, а сам процесс состоит в том, что время от времени система S скачком (мгновенно) перескакивает из одного состояния в другое.

37.