Классическое определение вероятности.

Вероятностью события A называют отношение числа благоприятствующих этому событию исходов к общему числу всех равновозможных несовместных элементарных исходов, образующих полную группу. Итак, вероятность события A определяется формулой

P(A) = m/n,

где m – число элементарных исходов, благоприятствующих A; n – число всех возможных элементарных исходов испытания.

События называют несовместными, если появление одного из них исключает появление других событий в одном и том же испытании.

Несколько событий образуют полную группу, если в результате испытаний появится хотя бы одно из них.

События называют равновозможными, если есть основание считать, что ни одно из них не является более возможным, чем другое.

Свойства вероятности.

Свойство 1. Вероятность достоверного события равна 1.

Действительно, если событие достоверно, то каждый элементарный исход испытания благоприятствует событию. В этом случае m = n, следовательно,

P(A) = m/n = n/n = 1.

Свойство 2. Вероятность невозможного события равна 0.

Действительно, если событие невозможно, то ни один из общего числа элементарных исходов испытания не благоприятствует событию. В этом случае m = 0, следовательно,

P(A) = m/n = 0/n = 0.

Свойство 3. Вероятность случайного события, есть положительное число заключенное между нулем и единицей.

Действительно, случайному событию благоприятствует лишь часть из общего числа элементарных исходов испытания. В этом случае 0 < m < n, значит, 0 < m/n < 1, следовательно,

0 < P(A) < 1.

Итак, вероятность любого события удовлетворяет двойному неравенству

0 <= P(A) <= 1.

3.

Произвольное пространство элементарных событий.

Множество всех элементарных событий, которые могут появиться в испытании, называют пространством элементарных событий Ω, а сами элементарные события – точками пространства Ω.

3.2. Алгебра и σ - алгебра множеств.

Алгебра событий.

Пусть Ω - пространство элементарных исходов некоторого случайного эксперимента (т.е. непустое множество произвольной природы). Мы собираемся определить набор подмножеств Ω, которые будут называться событиями, и затем задать вероятность как функцию, определенную только на множестве событий.

Итак, событиями мы будем называть не любые подмножества Ω, а лишь элементы некоторого выделенного набора подмножеств множества Ω. При этом необходимо позаботиться, чтобы этот набор подмножеств был замкнут относительно обычных операций над событиями, т.е. чтобы объединение, пересечение, дополнение событий снова давало событие.

Сигма-алгебра множеств.

σ-алгебра — алгебра множеств, замкнутая относительно операции счётного объединения.

Борелевские множества.

Борелевская сигма-алгебра — это минимальная сигма-алгебра, содержащая все открытые подмножества топологического пространства (впрочем, она содержит и все замкнутые).

Если не оговорено противное, в качестве топологического пространства выступает множество вещественных чисел.

Борелевская сигма-алгебра обычно выступает в роли сигма-алгебры случайных событий вероятностного пространства. В борелевской сигма-алгебре на прямой или на отрезке содержатся многие «простые» множества: все интервалы, полуинтервалы, отрезки и их счётные объединения.

Вероятность.

В современном математическом подходе классическая (т. е. не квантовая) вероятность задаётся аксиоматикой Колмогорова. Вероятностью называется мера P, которая задаётся на множестве X, называемом вероятностным пространством. Эта мера должна обладать следующими свойствами:

1. P(X) = 1, P(0) = 0.

2.

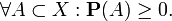
3. Мера P обладает свойством счётной аддитивности (сигма-аддитивности): если множества A₁, A₂, ..., A_n, ... не пересекаются, то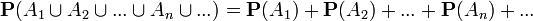

Из указанных условий следует, что вероятностная мера P также обладает свойством аддитивности: если множества A₁ и A₂ не пересекаются, то 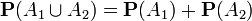. Для доказательства нужно положить все A₃, A₄, ... равными пустому множеству и применить свойство счётной аддитивности.

Вероятностная мера может быть определена не для всех подмножеств множества X. Достаточно определить её на сигма-алгебре Ω, состоящей из некоторых подмножеств множества X. При этом случайные события определяются как измеримые подмножества пространства X, то есть как элементы сигма-алгебры Ω.

4.

Геометрическая вероятность.

Что бы преодолеть недостаток классического определения вероятности, состоящий в том, что оно не применимо к испытаниям с бесконечным числом исходов, вводят геометрические вероятности – вероятности попадания точки в область (отрезок, часть плоскости и т.д.).

Если обозначить меру (длину, площадь, объем) области через mes, то вероятность попадания точки брошенной наудачу (в указанном выше смысле) в область g – часть области G, равна

P = mes g / mes G.

Замечание. В случае классического определения вероятность достоверного события (невозможного) события равна единице (нулю); справедливы и обратные утверждения (например, если вероятность события равна нулю, то событие невозможно). В случае геометрического определения вероятности обратные утверждения не имеют места. Например, вероятность попадания брошенной точки в одну определенную точку области G равна нулю, однако это событие может произойти, и, следовательно, не является невозможным.

5.

Условные вероятности.

Условной вероятностью P_A(B) называют вероятность события B, вычисленную в предположении, что событие A уже наступило

P_A(B) = P(AB)/P(A) (P(A) > 0).

Произведением двух событий A и B называют событие AB, состоящее в совместном появлении (совмещении) этих событий.