РАЗДЕЛ I. Теоретическая механика

РАЗДЕЛ I. Теоретическая механика

Введение

Техническая механика — комплексная дисциплина. Она вклю­чает три раздела: «Теоретическая механика», «Сопротивление ма­териалов», «Детали машин».

«Теоретическая механика» — раздел, в котором излагаются основные законы движения твердых тел и их взаимодействия.

В разделе «Сопротивление материалов» изучают­ся основы прочности материалов и методы расчетов элементов кон­струкций на прочность, жесткость и устойчивость под действием внешних сил.

В разделе «Технической механики» «Детали машин» рассматриваются основы конструирования и рас­чета деталей и сборочных единиц общего назначения.

Дисциплина «Техническая механика» является общепрофессио­нальной, обеспечивающей базовые знания при усвоении специальных дисциплин, изучаемых в дальнейшем.

ЛЕКЦИЯ 1

Тема 1.1. Основные понятия и аксиомы статики

Понятие о силе и системе сил

Сила — это мера механического взаимодействия материальных тел между собой.

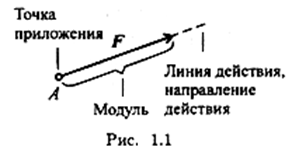Взаимодействие характеризуется величиной и направлением, т.е. сила есть величина векторная, характеризующа­яся

• точкой приложения (А),
• направлением (линией действия),
• вели­чиной (модулем) (рис. 1.1).

Силу измеряют в ньютонах, 1Н = 1кг • м/с².

Силы, действующие на тело (или систему тел), делятся на

· внешние и

· внутренние.

Внешние силы бывают

• активные и
• реактивные.

Активные силы вызывают перемещение тела,

реактиипые стремятся противодействовать перемещению тела под действием внешних сил.

Внутренние силы возникают в теле под действием внешних сил.

Совокупность сил, действующих на какое-либо тело, называют системой сил.

Эквивалентная система сил – система сил, действующая так же, как заданная.

Уравновешенной (эквивалентной нулю) системой сил называется такая система, которая, будучи приложенной к телу, не изменяет его состояния.

Систему сил, действующих на тело, можно заменить одной равнодействующей, действующей так, как система сил.

Задачи теоретической механики

Теоретическая механика — наука о механическом движении ма­териальных твердых тел и их взаимодействии. Механическое движе­ние понимается как перемещение тела в пространстве и во времени по отношению к другим телам, в частности к Земле.

Для удобства изучения теоретическую механику подразделяют на статику, кинематику и динамику.

· Статика изучает условия равновесия тел под действием сил.

· Кинематика рассматривает движение тел как перемещение в пространстве; характеристики тел и причины, вызывающие движе­ние, не рассматриваются.

· Динамика изучает движение тел под действием сил.

В отличие от физики теоретическая механика изучает законы движения некоторых абстрактных абсолютно твердых тел: здесь материалы, форма тел существенного значения не имеют. При движении абсолютно твердое тело не деформируется и не разрушается. В случае, когда размерами тела можно пренебречь, тело заменяют материальной точкой. Это упрощение, принятое в теоретической ме­ханике, значительно облегчает решение задач о движении.

Аксиомы статики

В результате обобщения человеческого опыта были установлены общие закономерности механического движения, выраженные в виде законов и теорем. Все теоремы и уравнения статики выводятся из нескольких исходных положений. Эти положения называют акси­омами статики.

Первая аксиома. Под действием уравновешенной системы сил абсолютно твердое тело или материальная точка находятся в равновесии или движутся равномерно и прямолинейно (закон инерции).

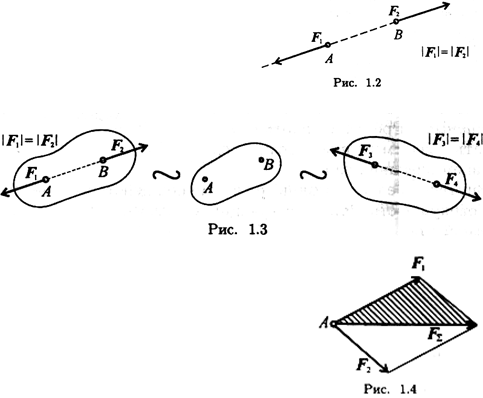
Вторая аксиома. Две силы, равные по модулю и направленные по одной прямой в разные стороны, уравновешивают­ся (рис. 1.2).

Третья аксиома. Не нарушая механического состояния тела, можно добавить или убрать уравновешенную систему сил (принцип отбрасывания систе­мы сил, эквивалентной нулю) (рис. 1.3).

Четвертая аксиома (правило параллелограмма сил). Равнодействующая двух сил, прило­женных в одной точке, приложена в той же точке и является диагональю параллело­грамма, построенного на этих силах как на сторонах (рис. 1.4).

Вместо параллелограмма можно постро­ить треугольник сил: силы вычерчивают одну за другой в любом порядке; равнодей­ствующая двух сил соединяет начало первой силы с концом второй.

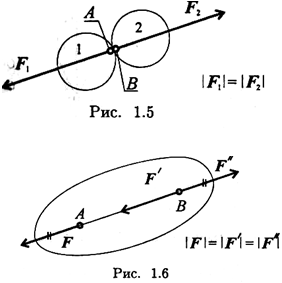
Пятая аксиома. При взаимодействии тел всякому действию соответствует равное и противоположно направленное противодействие (рис. 1.5).

Силы действующие и проти­водействующие всегда приложены к разным телам, поэтому они не уравновешиваются.

Силы, с которыми два тела дей­ствуют друг на друга, всегда равны по модулю и направлены вдоль одной прямой в разные стороны.

Следствие из второй и третьей аксиом. Силу, действующую на твердое тело, можно переме­щать вдоль линии ее действия(рис. 1.6).

Сила F приложена в точке А. Требуется перенести ее в точку В.

Используя третью аксиому, добавим в точке В уравновешенную систему сил (F'; F"). Образуется уравновешенная по второй аксиоме система сил(F; F"). Убираем ее и получим в точке В силу F", равную заданной F.

Связи и реакции связей

Все законы и теоремы статики справедливы для свободного твердого тела.

Все тела делятся на свободные и связанные.

Свободные тела — тела, перемещение которых не ограничено.

Связанные тела — тела, перемещение которых ограничено другими телами.

Тела_, ограничивающие перемещение других тел, называют свя­зями.

Силы, действующие от связей и препятствующие перемещению, называют реакциями связей.

Жесткий стержень.

На схемах стержни изображают толстой сплош­ной линией (рис. 1.9).

Стержень может быть сжат или растянут. Реакция стержня направлена вдоль стержня.

Стер­жень работает на растяжение или сжатие. Точное направление реакции определяют, мысленно убрав стержень и рассмотрев возможные перемещения тела без этой связи.

Возможным перемещением точки называется такое бесконечно малое мысленное перемещение, которое допуска­ется в данный момент наложенными на него связями.

Убираем стержень 1, в этом случае стержень 2 падает вниз. Сле­довательно, сила от стержня 1 (реакция) направлена вверх. Убираем стержень 2. В этом случае точка А опускается вниз, отодвигаясь от стены. Следовательно, реакция стержня 2 направлена к стене.

Шарнирная опора

Шарнир допускает поворот вокруг точки закрепления. Разли­чают два вида шарниров.

Подвижный шарнир. Стержень, закрепленный на шарнире, может поворачивать­ся вокруг шарнира, а точка крепления может перемещаться вдоль направляющей (площадки) (рис. 1.10).

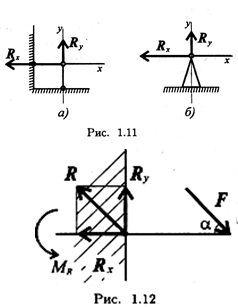Реакция подвижного шарни­ра направлена перпендикулярно опорной поверхности, т. к. не допускается только перемещение поперек опорной поверхности.

Неподвижный шарнир. Точка крепления переме­щаться не может. Стержень может свободно поворачи­ваться вокруг оси шарнира. Реакция такой опоры прохо­дит через ось шарнира, но неизвестна по направлению. Её принято изображать ввиде двух составляющих: горизонтальной и вертикальной (R_x, Ry) (рис. 1.11).

Защемление или «заделка». Любые перемещения точки крепле­ния невозможны.

Под действием внешних сил в опоре возникают реактивная сила и реак­тивный момент М_R, препятствующий повороту (рис. 1.12).

Реактивную силу принято представ­лять в виде двух составляющих вдоль осей координат

R = R_x + R_y

Примеры решения задач

Последовательность решения задач:

1. Выбрать тело (точку), равновесие которого следует рассматри­вать.
2. Освободить тело (шарнир) от связей и изобразить действую­щие на него активные силы и реакции отброшенных связей. Причем реакции стержней следует направить от шарнира, так как принято предполагать, что стержни растянуты.
3. Выбрать оси координат и составить уравнения равновесия, ис­пользуя условия равновесия системы сходящихся сил на плоскости ∑Xi = 0; ∑Yi = 0. Выбирая оси координат, следует учитывать, что полученные уравнения будут решаться проще, если одну из осей напра­вить перпендикулярно одной из неизвестных сил.
4. Определить реакции стержней из решения указанной системы уравнений.
5. Проверить правильность полученных результатов, решив уравне­ния равновесия относительно заново выбранных координат х и у.

Пример 1. Груз подвешен на стержнях и канатах и находится в равновесии (рис. 1.13). Изобразить систему сил, действующих на шарнир А.

Решение

1. 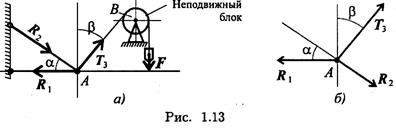Реакции стержней направлены вдоль стержней, реакции гибких связей направлены вдоль нитей в сторону натяжения (рис. 1.13, а).

2. Для определения точного направления усилий в стержнях мысленно убираем последовательно стержни 1 и 2. Анализируем воз­можные перемещения точки А.

Неподвижный блок с действующими на него силами не рассмат­риваем.

3. Убираем стержень 1, точка А поднимается и отходит от стены, следовательно, реакция стержня 1 направлена к стене.

4. Убираем стержень 2, точка А поднимается и приближается к стене, следовательно, реакция стержня 2 направлена от стены вниз.

5. Канат тянет вправо.

6. Освобождаемся от связей (рис. 1.13, б).

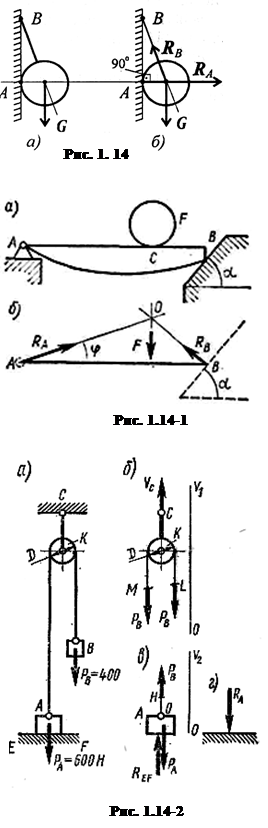
Пример 2. Шар подвешен на нити и опирается на стену (рис. 1.14а). Определить реакции нити и гладкой опоры (стенки).

Решение

1. Реакция нити — вдоль нити к точке В вверх (рис. 1.14, б).

2. Реакция гладкой опоры (стен­ки) — по нормали от поверхности опоры.

Пример 3. Представим, что на горизонтально расположенный брус АБ, собственной массой которого пренебрегаем, действует вертикальная нагрузка F, приложенная в точке С бруса (рис. 1.14-1, а). Левый конец бруса А прикреплен к опоре шарниром, а правый В опира­ется на гладкую наклонную плоскость.

Изобразим брус схематично отрезком АВ, как на рис. 1.14-1, б, и приложим к нему в точке С вертикальную силу F. В точке В со стороны наклонной плоскости к брусу приложена ее реакция R_B, направленная перпендикулярно плоскости; линии действия сил F и R_B пересекаются в точке О. Кроме этих сил на брус действует еще одна сила — реакция шарнирно-неподвижной опоры. А так как брус находится в равновесии, то линия действия третьей силы также пройдет через точку О, т. е. реакция R шарнир-но-неподвижной опоры направлена вдоль отрезка АО.

Примененный здесь метод рассуждения называется принципом освобождения тела от связей и замены связей их реакциями.

Пример 4. Определить усилие в стержне CD и силу давления груза А на опорную плоскость EF (рис. 1.14-2, а). Массой стержня CD, блока К, каната и трением каната о блок пренебречь.

Решение

Натяжение кана­та во всех его точках одина­ково и равно силе тяжести груза В, так как неподвиж­ный блок изменяет только направление силы, действую­щей на канат.

Рассмотрим равновесие си­стемы: стержень CD и блок К с прилегающим к нему отрезком каната ML. Отбросим связи и заменим их действие соответствующими реакциями (рис. 1.14-2, 6). Для полученной системы сил можно соста­вить только одно уравнение равновесия:

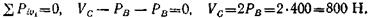
На рис. 1.14-2, в показаны силы, действующие на груз А с прилегающим к нему отрезком каната ОН. R_EF — реак­ция опорной плоскости.

Так как груз А находится в равновесии, то

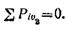
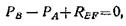
откуда

R_еf = Pa – Рв = 600 – 400 = 200 Н.

Сила давления груза А на опорную плоскость RA показана на рис, 1.14-2, г. Очевидно, R_A = R_EF = 200 H (сила действия равна силе противодействия).

Пример 5.Определить реакции стержней, удерживающих грузы F₁ = 70 кН и F₂ = 100 кН (рис. а). Массой стержней пренебречь.

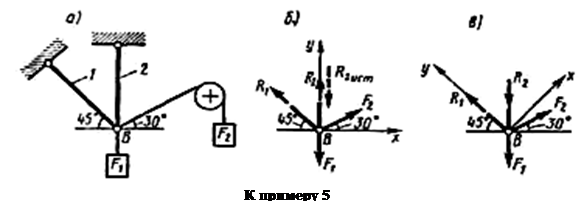Решение

1. Рассматриваем равновесие шарнира В (рис. а).

2. Освобождаем шарнир В от связей и изображаем действующие на него активные силы и реакции связей (рис. б).

3. Выбираем систему координат, совместив ось у по направлению С реакцией R₂ (рис. б) и составляем уравнения равновесия для системы сил, действующих на шарнир В:

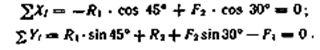
3. Определяем реакции стержней R₁ и R₂, решая уравнения.

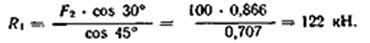
Подставляя найденное значение R₁ в уравнение (2), получаем

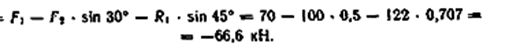
Знак минус перед значением R₂ указывает на то, что первоначально выбранное направление реакции неверное — следует направить реак­цию R₂ в противоположную сторону, т.е. к шарниру В (на рис. б истинное направление реакции R₂ показано штриховым вектором).

5. Проверяем правильность полученных результатов, выбрав новое расположение осей координат х и у (рис. а). Относительно этих осей составляем уравнения равновесия:

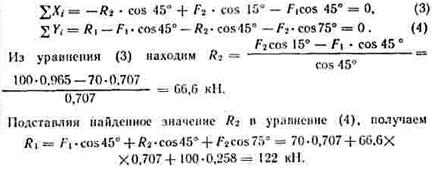
Значения реакций R₁ и R₂, полученные при решении уравнений (1) и (2), совпадают по величине и направлению со значениями, найденными из уравнений (3) и (4), следовательно, задача решена правильно.

Контрольные вопросы и задания

1. Какая из приведенных систем сил (рис. 1.15) уравновешена?

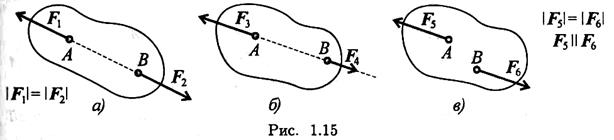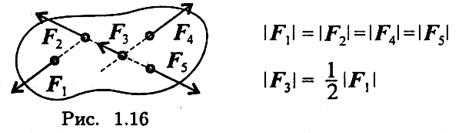2. Какие силы системы (рис. 1.16) можно убрать, не нарушая механического состояния тела:

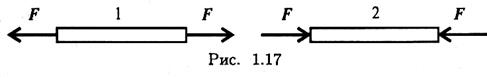3. Тела 1 и 2 (рис. 1.17) находятся в равновесии. Можно ли убрать действующие системы сил, если тела абсолютно твердые? Что изменится, если тела реальные, деформируемые?

4. Укажите возможное направление реакций в опорах (рис. 1.18).

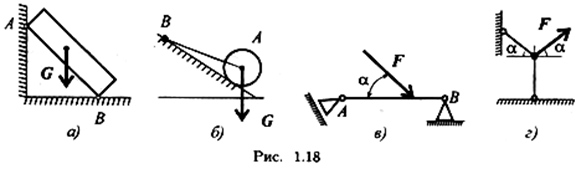
ЛЕКЦИЯ 2

ЛЕКЦИЯ 3

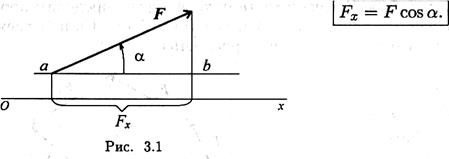
Проекция силы на ось

Проекция силы на ось определяется отрезком оси, отсекаемым перпендикулярами, опущенными на ось из начала и конца вектора (рис. 3.1).

Величина проекции силы на ось равна произведению модуля си­лы на косинус угла между вектором силы и положительным направ­лением оси. Таким образом, проекция имеет знак: положительный при одинаковом направлении вектора силы и оси и отрицательный при направлении в сторону отрицательной полуоси (рис. 3.2).

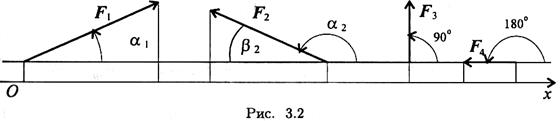F_1x = F₁ cos α₁ >0; F_2x = F₂cos α₂= - F₂ cos β₂;

cos α₂ = cos (180° — β₂)= — cos β₂

F_3x = F₃ cos90° = 0; F_4x = F₄ cos180° = - F₄.

Проекция силы на две взаимно перпендикулярные оси (рис. 3.3).

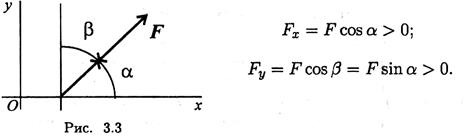Примеры решения задач

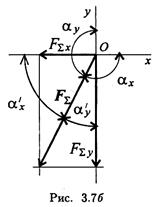
Пример 1. Определить величины и знаки проекций представленных на рис. 3.6 сил.

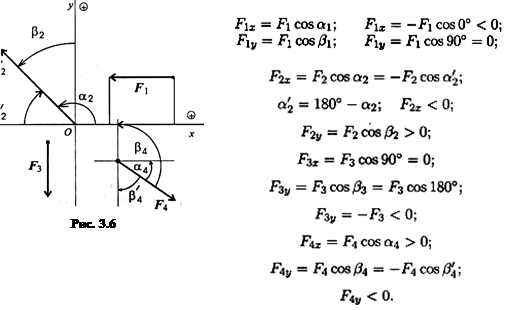Решение

Пример 2. Определить величину и направление равнодействующей плоской системы сходящихся сил аналитическим способом.

Решение

1.

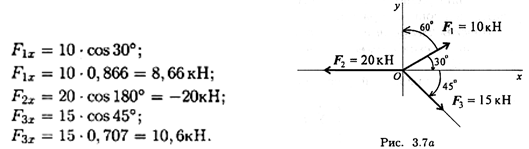Определяем проекции всех сил системы на Ох (рис. 3.7, а):

Сложив алгебраически проекции, получим проекцию равнодействующей на ось Ох.

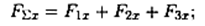F_∑x = 8,66 – 20 + 10,6 = - 0,735 кН

Знак говорит о том, что равнодействующая направлен влево.

2.

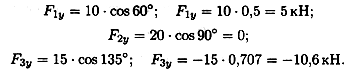Определяем проекции всех сил на ось Оу значения проекций, получим величину проекции Оу.

Сложив алгебраически значения проек­ций, получим величину проекции равнодей­ствующей на ось Оу.

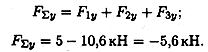Знак проекции соответствует на­правлению вниз. Следовательно, равно­действующая направлена влево и вниз (рис. 3.7б).

3. Определяем модуль равнодействую­щей по величинам проекций:

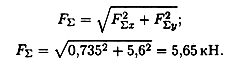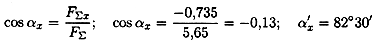4. Определяем значение угла равнодействующей с осью Ох:

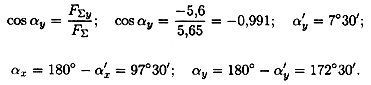и значение угла с осью Оу:

Пример 3. Система трех сил находится в равновесии. Известны проекции двух сил системы на взаимно перпендикулярные оси Ох и )у:

F_lx = 10 кН; F_2x = 5 кН;

F_1y = - 2 кН; F_2y = 6 кН.

Определить, чему равна и как направлена третья сила системы.

Решение

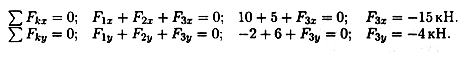1. Из уравнений равновесия системы определяем:

2.

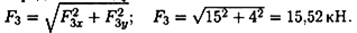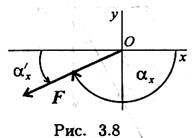По полученным величинам проекций определяем модуль силы:

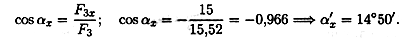Направление вектора силы относитель­но оси Ох (рис. 3.8):

Угол с осью Ох будет равен

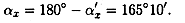Пример 4. Определить величину и направление реакций свя­зей для схемы, приведенной на рисунке, а под действием груза G = 30 кН. Проверить правильность определения реакций.

Решение

1. В задаче рассматривается равновесие тела, опи­рающегося на плоскость и подвешенного на нити. Заменим тело точкой 0, совпадающей с центром тяжести.

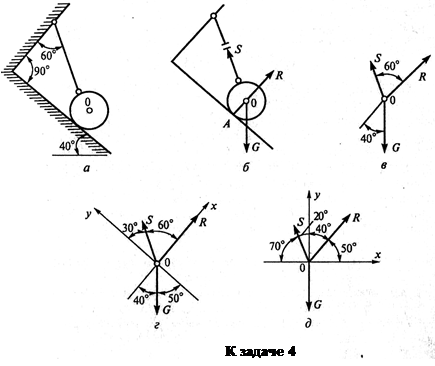2. Приложим к точке 0 активную силу, которой является соб­ственный вес тела G. Направим ее вниз (рис. б).

3. Мысленно отбросим связи — плоскость и нить. Заменим их действие на точку 0 реакциями связей. Реакция плоскости (обо­значим ее R) проходит по нормали к плоскости в точке А, а ре­акция или усилие в нити (обозначим ее S) — по нити от точки. Обе реакции и вес тела или линии их действия должны пересе­каться в точке 0.

Изобразим действующие силы в виде системы трех сходя­щихся сил на отдельном чертеже (рис. в).

4. Выберем положение системы координат. Начало координат совмещаем с точкой 0. Ось х совмещаем с направлением линии действия реакции R, а ось у направим перпендикулярно оси х (рис. г). Определим углы между осями координат и реакциями R и S. Обычно рис. б и в не выполняют отдельно, а сразу от рис. а переходят к рис. г. Можно было ось у совместить с усилием S, и ось х направить по углом 90°, тогда решение было бы другим.

5. Составим сумму проекций всех сил на оси координат:

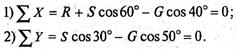
Решим систему уравнений. Из второго уравнения находим

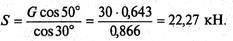
Из первого уравнения находим

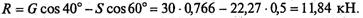
6.Проверим решение, для чего расположим оси координат, как показано на рис. д. Составим уравнения равновесия для вновь принятых осей:

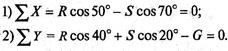
Решим систему уравнений способом подстановки.

Из первого уравнения найдем R:

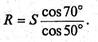
Подставим это выражение во второе уравнение:

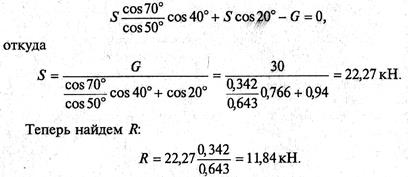
Очевидно, что при расположении осей, как показано на рис. д, вычисления оказались более сложными.

Ответ: R = 11,84 кН; S = 22,21 кН.

Пример 5. Определить усилия в нити и стержне кронштейна, показанного на рис. а, если G = 20 кН.

Решение

1. 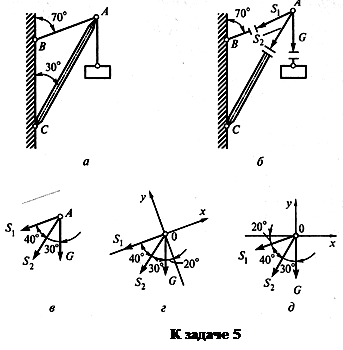Рассмотрим равновесие точки А (или узла А), в которой сходятся все стержни и нити.

2. Активной силой является вес груза G, направленный вниз (рис. б).

3. Отбросим связи: стержень и нить. Усилие в нити обозна­чим Sx и направим от точки А, так как нить может испытывать только растяжение. Усилие в стержне обозначим S₂ и тоже на­правим от точки А, предполагая что стержень АС растянут (рис. б).

Выполним на отдельном чертеже схему действия сил в точке А (рис. в).

4. Выберем положение системы координат. Начало коорди­нат совмещаем с точкой А (рис. г). Ось х совмещаем с лини­ей действия усилия S, а ось у располагаем перпендикулярно оси х. Укажем углы между осями координат и усилиями S₁.и S₂.

5. Составим уравнения равновесия.

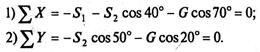
Из второго уравнения находим

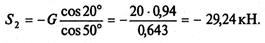
Из первого уравнения находим

Знак «минус» перед S₂ свидетельствует о том, что стержень АС не растянут, как предполагалось, а сжат.

6. Проверку решения предлагаем выполнить самостоятельно, расположив оси координат так, как показано на рис. д.

Ответ: S₁ = 15,56 кН, S₂ = - 29,24 кН (при принятом на черте­же направлении усилий).

Величина усилий зависит от углов наклона стержня и нити. Например, если на рис. а угол 70° заменить на 60°, сохранив угол 30°, то усилия будут равны: S₁= 20 кН, S₂ = - 34,64 кН. А при угле 50° S₁ = 29,26 кН, S₂ = - 44,8 кН. Оба усилия растут и становятся больше веса груза.

Пример 6. Как изменятся усилия в стержне и нити, если груз будет перекинут через блок, как показано на рис. а?

Остальные данные — в примере 5.

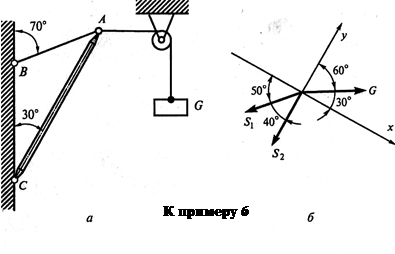Решение

1. Рассматриваемой тонкой остается точка А.

2. Активная сила (вес груза G) действует на точку горизонтально слева направо, так как груз перекинут через блок.

3. Усилия S₁ и S₂ прикладываем к точке А, как в примере 2.

4. Выбираем систему координат, как показано на рис. б.

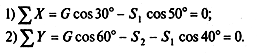5. Составляем и решаем уравнения равновесия:

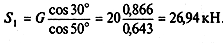Из первого уравнения находим

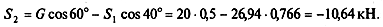Из второго уравнения находим

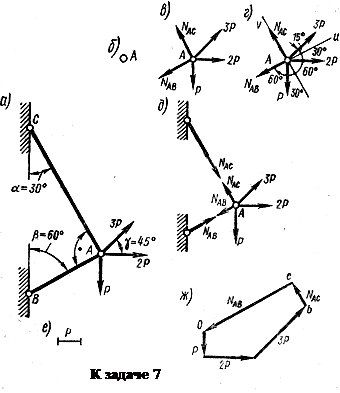Ответ: S₁ = 26,94 кН; S₂ = - 10,64 кН при принятом направлении усилий на чертеже. Усилие S₁ увеличилось, S₂ — уменьшилось, а знаки не изменились.

Пример 7. Определить усилия в стержнях (рис. а). Массой стержней пренебречь.

Решение

В соответствии с последовательностью действий, будем рассматривать равновесие узла А к которому приложены заданные нагрузки (Р, 2Р, 3Р) и искомые реакции стержней АВ и АС.

Освободим узел А от связей, заменим их действие искомыми реакциями N_АС, N_AB(рис. в). Получили плоскую систему сходящихся сил.

Выбираем систему координат (рис. г).

Сила N_AB перпендикулярна оси v, сила N_АС — оси и; поэтому в каждое уравнение равновесия войдет лишь одна неизвестная сила:

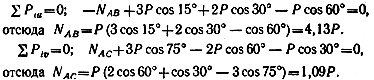Силы N_AB и N_АС получились положительными; это значит, что предполагаемые направления сил совпадают с действительными.

На рис. д показаны силы, действующие на узел (реакции стержней), и силы, действующие на стержни (усилия в стержнях или реакции узла).

Решим тот же пример графическим методом.

Полученная система сил (см. рис. в) находится в равновесии, и, следовательно, силовой многоугольник, построенный для этой системы сил, должен быть замкнутым.

Строим силовой многоугольник. Выбираем масштаб (рис. е). От точки О (рис. ж) в выбранном масштабе откладываем сначала силу Р, затем от конца вектора Р — силу 2Р, после чего от конца вектора 2Р — силу ЗР. Масштаб следует выбрать достаточно крупный, с тем чтобы при измерении отрезков (векторов), изображающих искомые силы, можно было получить их значения без большой погрешности. Через точку b проводим линию, параллельную стержню АС, и через точку О — линию, параллельную стержню АВ. Отрезки ОС и CB представляют собой искомые усилия. Направления задан­ных сил известны; стрелки, изображающие направления искомых сил, ставим таким образом, чтобы в векторном многоугольнике было единое на­правление обхода — в данном случае против часовой стрелки. Измерив отрезки к и Ос в со­ответствии с выбранным мас­штабом, находим абсолютные величины реакций; N_Acza\,2P\ N_ab~4,2P.

Решение примера выполнено двумя способами, которые (в пределах точности построений) дали совпадающие результаты. Очевидно, здесь никакой допол­нительной проверки решения не требуется.

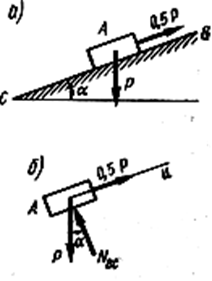Пример 8. Определить предельное значение угла а, при котором груз А (рис. а) будет находиться в по­кое. Плоскость ВС считать абсолютно гладкой.

Решение

Силы, действующие на груз А, представляют собой плоскую систему сходящихся сил. N_BC — реакция наклонной плоскости.

Если груз А находится в покое, то ∑P_to = 0, т.е.

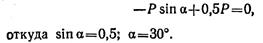
Контрольные вопросы и задания

1. Запишите выражение для расчета проекции силы F на ось Оу (рис. 3.9).

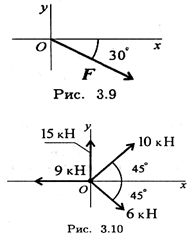
2. Определите сумму проекций сил системы на ось Ох (рис. 3.10).

4. Определите величину силы по известным проекциям:

F_x = 3 кН; F_y = 4 кН.

5.

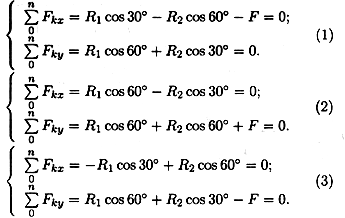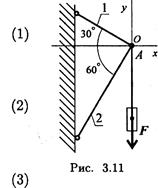Груз находится в равновесии (рис. 3.11). Какая система урав­нений равновесия для шарнира А записана верно?

Указания.

1. При ответе на вопросы 1 и 2 необходимо знать, что в выраже­ние для величины проекции силы на ось подставляется угол между вектором силы и положительной полуосью координат. Не забыть, что определяется алгебраическая сумма.

2. При ответе на вопрос 4 сначала следует определить возмож­ные направления реакций в стержнях, мысленно убирая по очереди стержни и рассматривая возможные перемещения (см. лекцию 1).

Затем записать алгебраические суммы проекций сил на оси О_х и О_у. Полученные уравнения сравнить с приведенными.

5. Ответьте на вопросы тестового задания.

Расчетные формулы

Равнодействующая системы сил

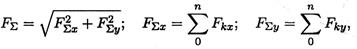
где F_∑x, F_∑y — проекции равнодействующей на оси координат; F_kx, F_ky — проекции векторов-сил системы на оси координат.

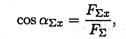
где — угол равнодействующей с осью Ох.

Условие равновесия

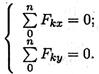
Если плоская система сходящихся сил находится в равновесии, мно­гоугольник сил должен быть замкнут.

Пример 1. Определение равнодействующей системы сил.

Определить равнодействующую плоской системы сходящихся сил аналитическим и геометрическим способами (рис. П1.1). Дано:

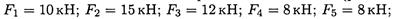
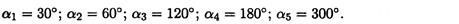
Решение

1. Определить равнодействующую аналитическим способом (рис.

2. Определить равнодействующую графическим способом.

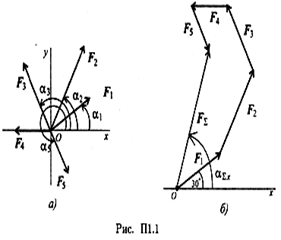
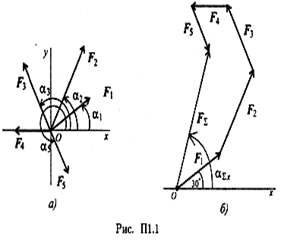
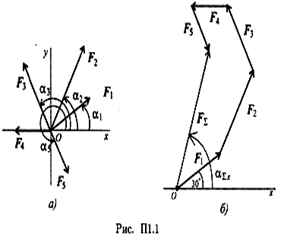
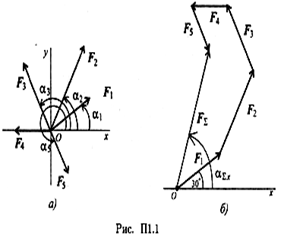
С помощью транспортира в масштабе 2 мм = 1 кН строим много­угольник сил (рис. П1.1б). Измерением определяем модуль равно­действующей силы и угол наклона ее к оси Ох.

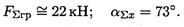
Результаты расчетов не должны отличаться более чем на 5%:

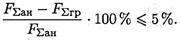
Расчетно-графическая работа №1. Определение равнодействующей плоской системы схо­дящихся сил аналитическим и геометрическим способами

Задание 1. Используя схему рис. П1.1а, определить равнодей­ствующую системы сил геометрическим способом

Пример 2. Решение задачи на равновесие аналитиче­ским способом.

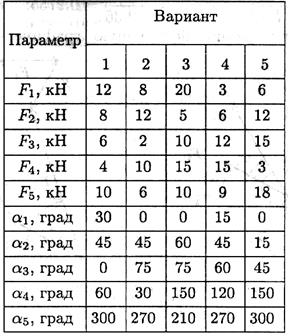
Грузы подвешены на стержнях и канатах и находятся в равно­весии. Определить реакции стержней АВ и СВ (рис. П1.2).

Решение

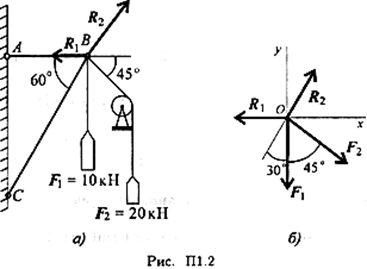
1. Определяем вероятные направления реакций (рис. П1.2а). Мысленно убираем стержень АВ, при этом стержень СВ опускается, следовательно, точка В отодвигается от стены: назначение стержня АВ — тянуть точку В к стене.

Если убрать стержень СВ, точка В опустится, следовательно, стержень СВ поддерживает точку В снизу — реакция направлена вверх.

2. Освобождаем точку В от связи (рис. П1.26).

3. Выберем направление осей координат, ось Ох совпадает с ре­акцией R₁.

4. Запишем уравнения равновесия точки В:

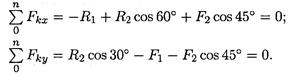
5. Из второго уравнения получаем:

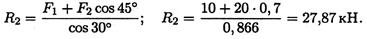
Из первого уравнения получаем:

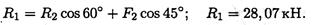
Вывод:стержень АВ растянут силой 28,07 кН, стержень СВ сжат силой 27,87 кН.

Примечание. Если при решении реакция связи окажется отрицательной, значит, вектор силы направлен в противоположную сторону.

В данном случае реакции направлены верно.

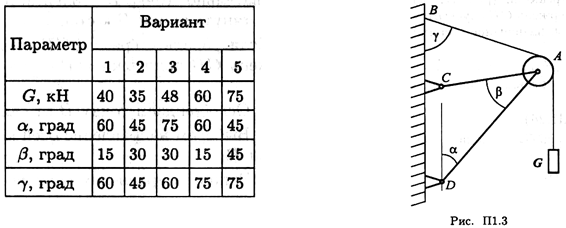Задание 2. Определить реакции стержней АС и AD (рис. П1.3) в аналитической форме.

При защите работ ответить на вопросы карт с тестовыми заданиями.

Задача 1

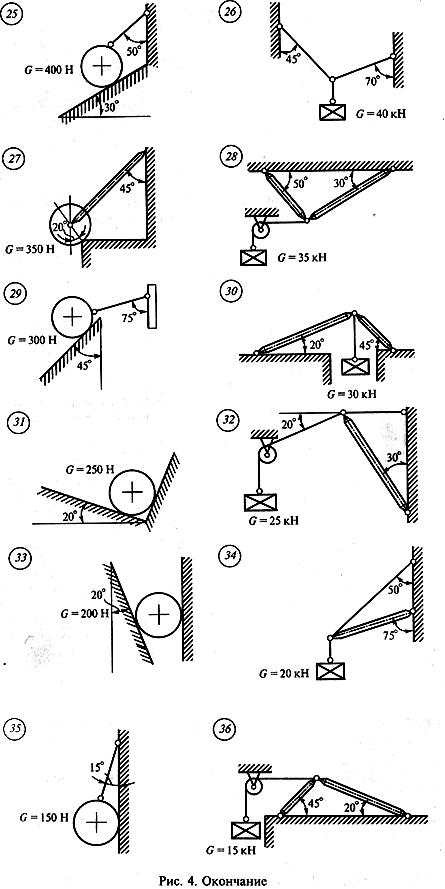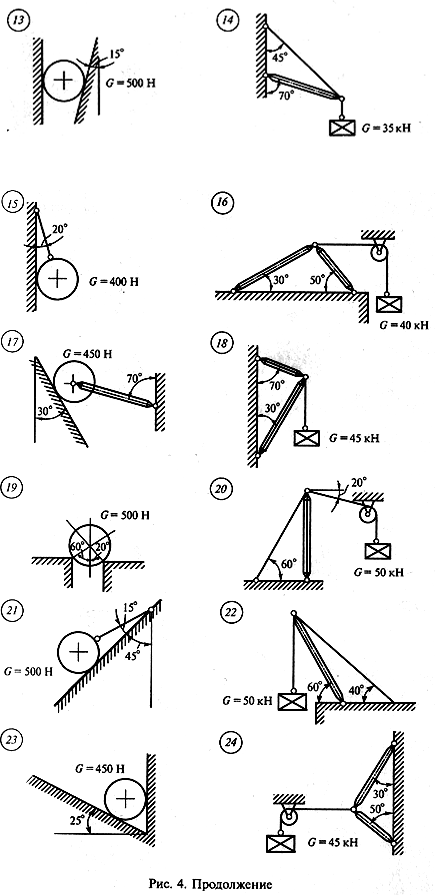
Задача 2. Определить реакции стержней, удерживающих грузы F₁ и F₂. Массой стержней пренебречь. Схему своего варианта см. на рисунке. Числовые данные своего варианта взять из таблицы.

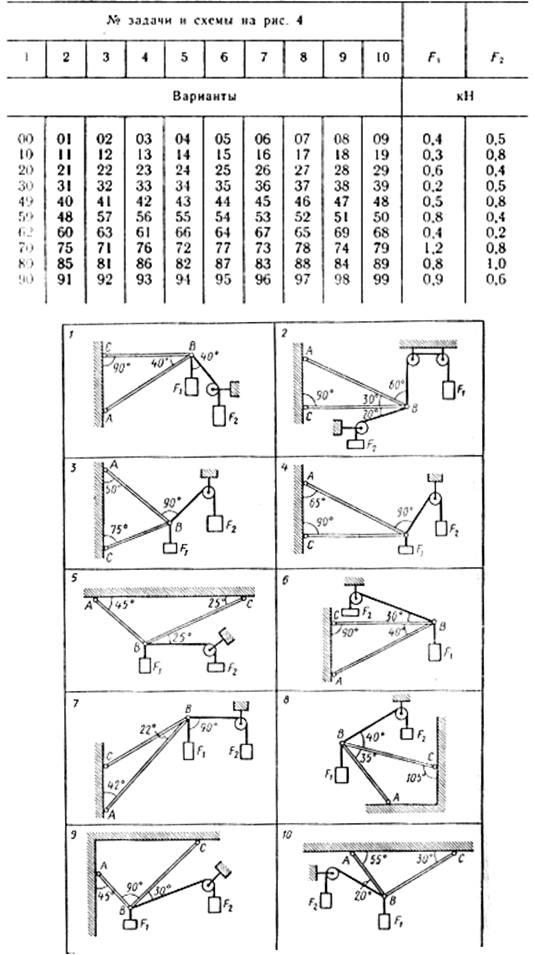ЛЕКЦИЯ 4

Пара сил, момент пары сил

Парой сил называется система двух сил, равных по модулю, параллельных и направ­ленных в разные стороны.

Рассмотрим систему сил (F, F¹), образую­щих пару.

1. Пара сил вызывает вращение тела, и ее действие на тело оценивается моментом.
2. Силы, входящие в пару, не уравновешива­ются, т. к. они приложены к двум точкам (рис. 4.1). Их действие на тело не может быть заменено одной силой (равнодействую­щей).
3. Момент пары сил численно равен произ­ведению модуля силы на расстояние между линиями действия сил (плечо пары).
4. Момент считают положительным, ес­ли пара вращает тело по часовой стрелке (рис. 4.1 б): M(F; F') = Fa; М > 0.
5. Плоскость, проходящая через линии действия сил пары, называется плоскостью действия пары.

Свойства пар (без доказательств):

1. Пару сил можно перемещать в плоскости ее действия.
2. Эквивалентность пар. Две пары, моменты которых равны, (рис. 4.2) эквивалентны (действие их на тело аналогично).
3. Сложение пар сил. Систему пар сил можно заменить равно­действующей парой.

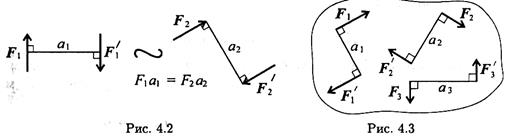Момент равнодействующей пары равен алгебраической сумме моментов пар, составляющих систему (рис. 4.3):

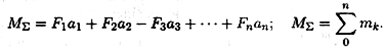4. Равновесие пар.

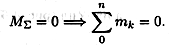Для равновесия пар необходимо и достаточно, чтобы алгебраи­ческая сумма моментов пар системы равнялась нулю:

Примеры решения задач

Пример 1. Дана пара сил |F₁| = \F₁¹\ =42 кН; плечо2 м. Заменить заданную пару сил эквивалентной парой с плечом 0,7 м (рис. 4.5).

Решение

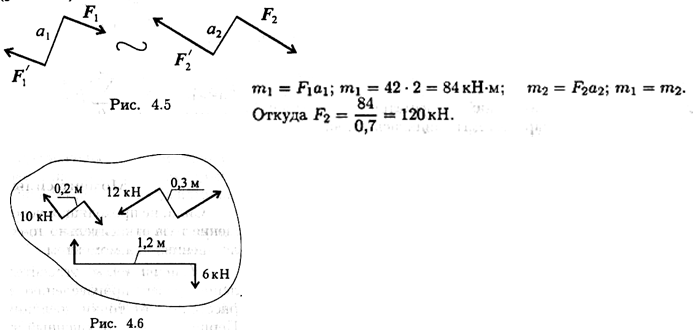
Пары сил эквив