Вопрос №1.Перестановка, размещение и сочетание без повторений
Вопрос №1.Перестановка, размещение и сочетание без повторений
Одно и то же множество можно упорядочить различными способами. Например, множество студентов группы можно упорядочить по возрасту, росту, алфавиту, успеваемости… Множества всех перестановок из n элементов будем обозначать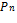 
Теорема.Число различных перестановокиз n элементов определяется по формуле: P=1*2*3*…*n=n! (n- факториал)
4!=1*2*3*4=24
Считают ,что 0!=1
Задача. Сколько различных пятизначных чисел можно записать с помощью цифр 01234,если ни одна НЕ должна повторяться дважды?
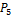=1*2*3*4*5=120
Из 120 вычтем числа, которые начинаются на 0(т.е. 4-хзначные числа).Для этого цифру 0 закрепим на 1 месте и останется выяснить сколько 4-хзначных чисел можно составить из 1234;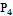 
=1*2*3*4=24
120-24=96
Всякое упорядоченное k-элементное подмножество n элементов множества (k≤n) называется размещениемиз n-элементов по k.
Два размещения считаются различными, если они отличаются друг от друга хотя бы одним элементом или состоят из одних и тех же элементов ,но расположены в разном порядке. Число различных размещений из n элементов по k элемявыыентов обозначается символом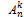 
Теорема . =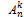 
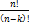(размещение) порядок играет роль
Задача.1) Сколькими способами можно распределить 5 путёвок в различные дома отдыха, если отдохнуть желают 12 человек. Из 12 нужно выбрать 5, а затем между ними распределить путевки, это размещение из 12 элементов по 5
= 
= 
= 
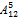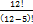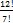=95040
Задача.2) Сколько 4-хзначных чисел можно составить из цифр 1234567,если ни одна цифра НЕ должна повторяться больше одного раза.
= 
= 
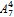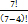=4*5*6*7=840
Теорема.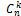 
= 
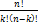(сочетания) порядок НЕ играет роль
Задача. Из группы студентов ,состоящих из 25 человек, надо составить команду из 4-х чел, для участия в соревнованиях. Сколькими способами это можно сделать. Порядок НЕ играет роли.
= 
= 
= 
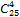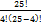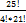=12650
Вопрос №3. Позиционные и непозиционные системы счисления
Для наименования записи чисел и выполнения действий над ними в математике называется системой счисления(СЧ).
Для записи натуральных чисел применялись различные СЧ, которые можно разделить на позиционные и непозиционные.
В непозициооных СЧ значение каждого символа не зависит от его места в записи числа. Примером является римская нумерация чисел в которой: I-единица, V- пять, X- десять, L- пятьдесят, C-сто, D- пятьсот, M- тысяча.
Правило записи чисел в римской системе заключается в следующем:
А) если знак, изображающий меньшее число, стоит после знака изображающего болешее число, то производится сложение;
V I= 5+1=6
X V=10+5=15
Б) если знак, изображающий меньшее число, стоит перед знаком изображающий большее число, то производится вычитание;
I V=5-1=4
I X=10-1=9
Непозиционной системой считалась также греческая система, в которой Альфа (α)=1,Бета (β)=2, Гамма (γ)=3, …
В непозиционных СЧ записи получаются длинными, умножение и деление в письменном виде производить невозможно.
На смену к непозиционным системам пришли позиционные СЧ, в которых значения символов зависит от места или позиции в записи числа.
Пр.
| 28 | ||||||
| - | ||||||
| 58 | ||||||
| 58 |
| (11) | 813 | ||||
| - | |||||
| (10) | 513 | ||||
| 313 |
Пр.Составим таблицу умножения чисел в пятеричной системе.
Равные комплексные числа
- два комплексных числа Z1 = a1 + b1 * i
Z2 = a2 + b2 * i
A1 = a2 ;b1 = b2
Вопрос №1.Перестановка, размещение и сочетание без повторений
Одно и то же множество можно упорядочить различными способами. Например, множество студентов группы можно упорядочить по возрасту, росту, алфавиту, успеваемости… Множества всех перестановок из n элементов будем обозначать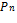
Теорема.Число различных перестановокиз n элементов определяется по формуле: P=1*2*3*…*n=n! (n- факториал)
4!=1*2*3*4=24
Считают ,что 0!=1
Задача. Сколько различных пятизначных чисел можно записать с помощью цифр 01234,если ни одна НЕ должна повторяться дважды?
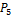=1*2*3*4*5=120
Из 120 вычтем числа, которые начинаются на 0(т.е. 4-хзначные числа).Для этого цифру 0 закрепим на 1 месте и останется выяснить сколько 4-хзначных чисел можно составить из 1234; 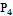=1*2*3*4=24
120-24=96
Всякое упорядоченное k-элементное подмножество n элементов множества (k≤n) называется размещениемиз n-элементов по k.
Два размещения считаются различными, если они отличаются друг от друга хотя бы одним элементом или состоят из одних и тех же элементов ,но расположены в разном порядке. Число различных размещений из n элементов по k элемявыыентов обозначается символом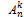
Теорема . 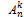= 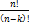(размещение) порядок играет роль
Задача.1) Сколькими способами можно распределить 5 путёвок в различные дома отдыха, если отдохнуть желают 12 человек. Из 12 нужно выбрать 5, а затем между ними распределить путевки, это размещение из 12 элементов по 5
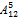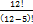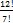= = = =95040
Задача.2) Сколько 4-хзначных чисел можно составить из цифр 1234567,если ни одна цифра НЕ должна повторяться больше одного раза.
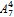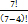= = =4*5*6*7=840
Теорема. 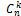= 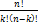(сочетания) порядок НЕ играет роль
Задача. Из группы студентов ,состоящих из 25 человек, надо составить команду из 4-х чел, для участия в соревнованиях. Сколькими способами это можно сделать. Порядок НЕ играет роли.
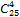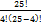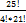= = = =12650