Численные методы решения нелинейного уравнения с одной неизвестной
Курсовая работа
по дисциплине Информатика
на тему:
Нелинейные уравнения, системы уравнений, аппроксимация и интерполяция
Вариант: 53
Выполнил: Володкин А.С.
Проверил: Федосеева Т.А.
Содержание
1. Численные методы решения нелинейного уравнения с одной неизвестной 3
1.1. Постановка задачи. 3
1.2. Шаговый метод. 3
1.3. Метод половинного деления. 4
1.4. Метод Ньютона. 5
1.5. Метод простой итерации. 6
2. Численные методы решения системы линейных уравнений. 7
2.1. Постановка задачи. 7
2.2. Метод Гаусса. 7
2.3. Метод простой итерации. 8
2.4. Метод Зейделя. 10
3. Численные методы решения задачи аппроксимации. 12
3.1. Постановка задачи. 12
3.2. Решение задачи интерполяции (полиномы первой и второй степени) методом неопределенных коэффициентов. 12
3.3. Решение задачи интерполяции с использованием полинома Лагранжа 14
3.4. Решение задачи аппроксимации методом наименьших квадратов. 15
Численные методы решения нелинейного уравнения с одной неизвестной
Постановка задачи
Дано нелинейное уравнение 1x2-8x + 12 = 0, интервал поиска корня [4;7] и шаг 0,3.
Требуется:
· отделить первый корень уравнения шаговым методом;
· уточнить значение корня методом половинного деления с точностью ε = 0,01;
· уточнить значение корня методом Ньютона с точностью ε = 0,001;
· уточнить значение корня методом простой итерации с точностью ε = 0,03.
Шаговый метод
Шаговый метод отделения корней основан на следующих теоремах:
Теорема 1.
Если функция F(x), определяющая уравнение F(x)=0, на концах отрезка [a;b] принимает значения разных знаков, т.е. F(a)·F(b)<0,то на этом отрезке содержится, по крайней мере, один корень уравнения.
Теорема 2.
Если функция F(x) строго монотонна, то корень на [a;b] единственный (F´(a) F´(b)>0).
Таким образом, для отделения корней пошаговым методом, вычисляется значение функции F(x), начиная с точки x=a, двигаясь вправо с некоторым шагом h. Если F(x) F(x+h)<0, то на отрезке [x; x+h]существует корень, а если функция F(x) еще и строго монотонна, то корень единственный. Если F(xk)=0, xk-точный корень.
Дано нелинейное уравнение:
1x2-8x + 12 = 0,
интервал поиска корня [4;7] и шаг 0,3. Отделим первый корень данного уравнения. Для этого построим таблицу в соответствии с алгоритмом метода:
| a | b | f(a) | f(b) |
| 4,3 | -4 | -3,91 | |
| 4,3 | 4,6 | -3,91 | -3,64 |
| 4,6 | 4,9 | -3,64 | -3,19 |
| 4,9 | 5,2 | -3,19 | -2,56 |
| 5,2 | 5,5 | -2,56 | -1,75 |
| 5,5 | 5,8 | -1,75 | -0,76 |
| 5,8 | 6,1 | -0,76 | 0,41 |
| 6,1 | 6,4 | 0,41 | 1,76 |
| 6,4 | 6,7 | 1,76 | 3,29 |
| 6,7 | 3,29 |
f(5,8)=-0,76<0, f(6,1)=0,41>0 Þ f(5,8)*f(6,1)<0, следовательно, корень лежит на промежутке от 5,8 до 6,1.
Метод половинного деления
Уточним корень методом половинного деления. Метод основан на последовательном сужении интервала, содержащего единственный корень уравнения F(x)=0 до тех пор, пока не будет достигнута заданная точность ε. Пусть задан отрезок [a,b], содержащий один корень уравнения.
Алгоритм:
• Определить новое приближение корня x в середине отрезка [a,b]: x=(a+b)/2.
• Найти значения функции в точках a и x : F(a) и F(x).
• Проверить условие F(a)F(x)<0. Если условие выполнено, то корень расположен на отрезке [a,x]. В этом случае необходимо точку b переместить в точку x(b=x). Если условие не выполнено, то корень расположен на отрезке [x,b]. В этом случае необходимо точку a переместить в точку x(a=x).
• Перейти к пункту 1 и вновь поделить отрезок пополам. Алгоритм продолжить до тех пор, пока не будет выполнено условие ⎪F(x)⎪<ε.
Построим таблицу в соответствии с алгоритмом:
| a | х | b | f(a) | f(х) | f(a)*f(х)<0 |
| 5,8 | 5,95 | 6,1 | -0,76 | -0,1975 | Нет |
| 5,95 | 6,025 | 6,1 | -0,198 | 0,100625 | Да |
| 5,95 | 5,9875 | 6,025 | -0,198 | -0,0498438 | Нет |
| 5,9875 | 6,0063 | 6,025 | -0,05 | 0,02503906 | Да |
| 5,9875 | 5,9969 | 6,0063 | -0,05 | -0,0124902 | Нет |
| 5,9969 | 6,0016 | 6,0063 | -0,012 | 0,00625244 | Стоп |
Остановка итераций, так как 0<0,01. x=6.0016 – корень данного уравнения.
Метод Ньютона
Уточним корень уравнения методом Ньютона (касательных).
Первая и вторая производная в нашем случае положительны на отрезке изоляции корня [4;7]:
f’(x)= 2x – 8; f”(x) = 2. f(5.8) = -0.76; f(6.1) = 0.41.
Следовательно, в качестве начального приближения к корню выбираем точку x0 = а = 5,8.
| i | xi | f(хi) | f'(хi) | f(хi)<0,001 |
| 5,8 | -0,76 | 3,6 | Нет | |
| 6,011111 | 0,044567901 | 4,022222222 | Нет | |
| 6,000031 | 0,000122776 | 4,000061387 | Да |
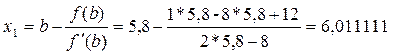
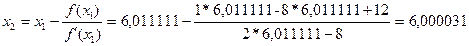
Итерации закончились. Искомый корень найден и равен 6,000031. Для проверки расчетов вычислим значение функции в этой точке:
f(6,011111) = 0
.
Метод простой итерации
Уточним корень методом простой итерации.
1x2-8x +12 = 0
Тогда ϕ(x) = 1x2 – 8x +12; ϕ′(x) = 2x – 8; ϕ′(5,8) = -0,76; ϕ′(6,1) = -0,41. Условие сходимости не выполнено, поскольку |-5,8| > 1 и |-6,1| > 1.
Запишем исходное уравнение в виде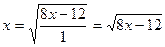 
. Тогда
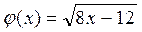
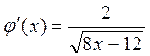ϕ′(5,8) = 0,341; ϕ′(6,1) = 0,329.
Условие сходимости выполнено.
В качестве начального приближения, возьмем первый из концов отрезка: x0=5,8. Составим таблицу, в соответствии с алгоритмом метода:
| i | xi | f(хi) | |f(хi)|<0,03 |
| 5,8 | -0,760000 | Нет | |
| 5,8652 | -0,521211 | Нет | |
| 5,9094 | -0,354126 | Нет | |
| 5,9393 | -0,239098 | Нет | |
| 5,9594 | -0,160756 | Нет | |
| 5,9729 | -0,107779 | Нет | |
| 5,9819 | -0,072125 | Нет | |
| 5,9879 | -0,048204 | Нет | |
| 5,9919 | -0,032190 | Нет | |
| 5,9946 | -0,021484 | Да |
Уточненное по методу итераций значение корня: 5,9946.
Постановка задачи
Дана система линейных уравнений:
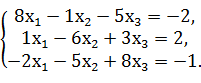
Требуется решить систему уравнений, используя:
• метод Гаусса (решение в обыкновенных дробях);
• метод простой итерации (3 итерации);
• метод Зейделя (3 итерации).
Метод Гаусса
1. Прямой ход метода Гаусса:
Запишем систему в виде матрицы, включив коэффициенты уравнений и свободные члены:
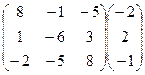
Работаем со столбцом №1
Умножим 1-ую строку на (1/8) и добавим к 3-ей:
| -0,125 | -0,625 | -0,25 | |
| -5,875 | 3,625 | 2,25 | |
| -5,25 | 6,75 | -1,5 |
Работаем со столбцом №2
Умножим 2-ую строку на (-5,875) и добавим ко 3-ой:
| -0,125 | -0,625 | -0,25 | |
| -0,617 | -0,383 | ||
| 3,5106 | -3,5106 |
Умножим 3-ую строку на (3,5106):
| -0,125 | -0,625 | -0,25 | |
| -0,617 | -0,383 | ||
| -1 |
Получим единицы на главной диагонали. Для этого всю строку делим на соответствующий элемент главной диагонали:
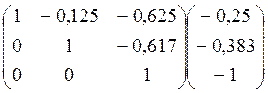
Теперь исходную систему можно записать как:
x1 = -0,25- ( - 0,125x2 – 0,625x3)
x2 = -0,383 - ( - 0,617x3)
x3 = -1
2. Обратный ход метода Гаусса:
Из 3-ой строки выражаем x3
Из 2-ой строки выражаем x2
x2 = -1
Из 1-ой строки выражаем x1
x2 = -1
Получили ответ: (-1,-1,-1).
Метод простой итерации
Проверим условие сходимости: Для сходимости метода необходимо и достаточно, чтобы в матрице A абсолютные значения всех диагональных элементов были больше суммы модулей всех остальных элементов в соответствующей строке.
Наша система имеет вид:
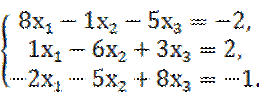
|8|>|-1|+|-5|-да
|-6|>|1|+|3|-да
|8|>|-2|+|-6|-да
Условие сходимости выполняется.
Выберем начальное приближение: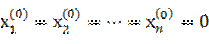 
Для организации итерационного процесса запишем систему в приведенном виде:
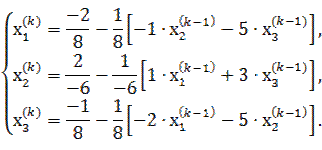
Получим:
x1=-0,25-0,125x2-0,625x3
x2=-0,33-0,17x1-0,5x3
x3=-0,125+0,25x1-0,625x2
Проведем три итерации:
1 итерация:
x1 = -0,25
x2 = -0,333333333
x3 = -0,125
2 итерация:
x1 = -0,369791667
x2 = -0,4375
x3 = -0,395833333
3 итерация:
x1 = -0,552083333
x2 = -0,592881944
x3 = -0,490885417
Результат после выполнения трех итераций: (-0,552;-0,593;-0,491).
Метод Зейделя
Наша система имеет вид:
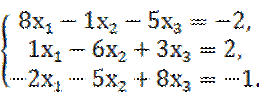
Для организации итерационного процесса запишем систему в приведенном виде:
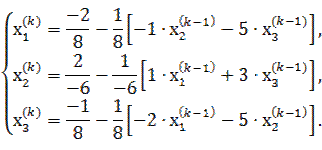
Получим:
x1=-0,25-0,125x2-0,625x3
x2=-0,33-0,17x1-0,5x3
x3=-0,125-0,25x1-0,625x2
Проведем три итерации:
1 итерация:
x1 = -0,25
x2 = -0,375
x3 = -0,625
2 итерация:
x1 = -0,6875
x2 = -0,760416667
x3 = -0,772135417
3 итерация:
x1 = -0,827636719
x2 = -0,857340495
x3 = -0,867746989
Результат после выполнения трех итераций:
(-0,828;-0,857;-0,868).
Постановка задачи
| x | -3 | -1 | |||
| f(x) | -3 | -2 |
Требуется:
• решить задачу интерполяции методом неопределенных коэффициентов (кусочно-линейная для каждой последовательной пары точек 1+2, 2+3, 3+4, 4+5, кусочно-параболическая интерполяция для каждой последовательной тройки точек 1+2+3, 3+4+5)
• решить задачу интерполяции с использованием полинома Лагранжа(кусочно-линейная для каждой последовательной пары точек 1+2,2+3,3+4,4+5, кусочно-параболическая интерполяция для каждой последовательной тройки точек 1+2+3, 3+4+5)
• решить задачу аппроксимации полиномом 1-й и 2-й степени методом наименьших квадратов для всех точек 1+2+3+4+5
Курсовая работа
по дисциплине Информатика
на тему:
Нелинейные уравнения, системы уравнений, аппроксимация и интерполяция
Вариант: 53
Выполнил: Володкин А.С.
Проверил: Федосеева Т.А.
Содержание
1. Численные методы решения нелинейного уравнения с одной неизвестной 3
1.1. Постановка задачи. 3
1.2. Шаговый метод. 3
1.3. Метод половинного деления. 4
1.4. Метод Ньютона. 5
1.5. Метод простой итерации. 6
2. Численные методы решения системы линейных уравнений. 7
2.1. Постановка задачи. 7
2.2. Метод Гаусса. 7
2.3. Метод простой итерации. 8
2.4. Метод Зейделя. 10
3. Численные методы решения задачи аппроксимации. 12
3.1. Постановка задачи. 12
3.2. Решение задачи интерполяции (полиномы первой и второй степени) методом неопределенных коэффициентов. 12
3.3. Решение задачи интерполяции с использованием полинома Лагранжа 14
3.4. Решение задачи аппроксимации методом наименьших квадратов. 15
Численные методы решения нелинейного уравнения с одной неизвестной
Постановка задачи
Дано нелинейное уравнение 1x2-8x + 12 = 0, интервал поиска корня [4;7] и шаг 0,3.
Требуется:
· отделить первый корень уравнения шаговым методом;
· уточнить значение корня методом половинного деления с точностью ε = 0,01;
· уточнить значение корня методом Ньютона с точностью ε = 0,001;
· уточнить значение корня методом простой итерации с точностью ε = 0,03.
Шаговый метод
Шаговый метод отделения корней основан на следующих теоремах:
Теорема 1.
Если функция F(x), определяющая уравнение F(x)=0, на концах отрезка [a;b] принимает значения разных знаков, т.е. F(a)·F(b)<0,то на этом отрезке содержится, по крайней мере, один корень уравнения.
Теорема 2.
Если функция F(x) строго монотонна, то корень на [a;b] единственный (F´(a) F´(b)>0).
Таким образом, для отделения корней пошаговым методом, вычисляется значение функции F(x), начиная с точки x=a, двигаясь вправо с некоторым шагом h. Если F(x) F(x+h)<0, то на отрезке [x; x+h]существует корень, а если функция F(x) еще и строго монотонна, то корень единственный. Если F(xk)=0, xk-точный корень.
Дано нелинейное уравнение:
1x2-8x + 12 = 0,
интервал поиска корня [4;7] и шаг 0,3. Отделим первый корень данного уравнения. Для этого построим таблицу в соответствии с алгоритмом метода:
| a | b | f(a) | f(b) |
| 4,3 | -4 | -3,91 | |
| 4,3 | 4,6 | -3,91 | -3,64 |
| 4,6 | 4,9 | -3,64 | -3,19 |
| 4,9 | 5,2 | -3,19 | -2,56 |
| 5,2 | 5,5 | -2,56 | -1,75 |
| 5,5 | 5,8 | -1,75 | -0,76 |
| 5,8 | 6,1 | -0,76 | 0,41 |
| 6,1 | 6,4 | 0,41 | 1,76 |
| 6,4 | 6,7 | 1,76 | 3,29 |
| 6,7 | 3,29 |
f(5,8)=-0,76<0, f(6,1)=0,41>0 Þ f(5,8)*f(6,1)<0, следовательно, корень лежит на промежутке от 5,8 до 6,1.
Метод половинного деления
Уточним корень методом половинного деления. Метод основан на последовательном сужении интервала, содержащего единственный корень уравнения F(x)=0 до тех пор, пока не будет достигнута заданная точность ε. Пусть задан отрезок [a,b], содержащий один корень уравнения.
Алгоритм:
• Определить новое приближение корня x в середине отрезка [a,b]: x=(a+b)/2.
• Найти значения функции в точках a и x : F(a) и F(x).
• Проверить условие F(a)F(x)<0. Если условие выполнено, то корень расположен на отрезке [a,x]. В этом случае необходимо точку b переместить в точку x(b=x). Если условие не выполнено, то корень расположен на отрезке [x,b]. В этом случае необходимо точку a переместить в точку x(a=x).
• Перейти к пункту 1 и вновь поделить отрезок пополам. Алгоритм продолжить до тех пор, пока не будет выполнено условие ⎪F(x)⎪<ε.
Построим таблицу в соответствии с алгоритмом:
| a | х | b | f(a) | f(х) | f(a)*f(х)<0 |
| 5,8 | 5,95 | 6,1 | -0,76 | -0,1975 | Нет |
| 5,95 | 6,025 | 6,1 | -0,198 | 0,100625 | Да |
| 5,95 | 5,9875 | 6,025 | -0,198 | -0,0498438 | Нет |
| 5,9875 | 6,0063 | 6,025 | -0,05 | 0,02503906 | Да |
| 5,9875 | 5,9969 | 6,0063 | -0,05 | -0,0124902 | Нет |
| 5,9969 | 6,0016 | 6,0063 | -0,012 | 0,00625244 | Стоп |
Остановка итераций, так как 0<0,01. x=6.0016 – корень данного уравнения.
Метод Ньютона
Уточним корень уравнения методом Ньютона (касательных).
Первая и вторая производная в нашем случае положительны на отрезке изоляции корня [4;7]:
f’(x)= 2x – 8; f”(x) = 2. f(5.8) = -0.76; f(6.1) = 0.41.
Следовательно, в качестве начального приближения к корню выбираем точку x0 = а = 5,8.
| i | xi | f(хi) | f'(хi) | f(хi)<0,001 |
| 5,8 | -0,76 | 3,6 | Нет | |
| 6,011111 | 0,044567901 | 4,022222222 | Нет | |
| 6,000031 | 0,000122776 | 4,000061387 | Да |
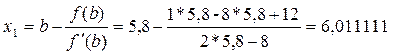
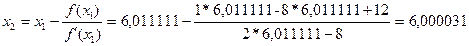
Итерации закончились. Искомый корень найден и равен 6,000031. Для проверки расчетов вычислим значение функции в этой точке:
f(6,011111) = 0
.
Метод простой итерации
Уточним корень методом простой итерации.
1x2-8x +12 = 0
Тогда ϕ(x) = 1x2 – 8x +12; ϕ′(x) = 2x – 8; ϕ′(5,8) = -0,76; ϕ′(6,1) = -0,41. Условие сходимости не выполнено, поскольку |-5,8| > 1 и |-6,1| > 1.
Запишем исходное уравнение в виде 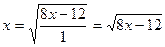. Тогда
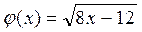
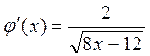ϕ′(5,8) = 0,341; ϕ′(6,1) = 0,329.
Условие сходимости выполнено.
В качестве начального приближения, возьмем первый из концов отрезка: x0=5,8. Составим таблицу, в соответствии с алгоритмом метода:
| i | xi | f(хi) | |f(хi)|<0,03 |
| 5,8 | -0,760000 | Нет | |
| 5,8652 | -0,521211 | Нет | |
| 5,9094 | -0,354126 | Нет | |
| 5,9393 | -0,239098 | Нет | |
| 5,9594 | -0,160756 | Нет | |
| 5,9729 | -0,107779 | Нет | |
| 5,9819 | -0,072125 | Нет | |
| 5,9879 | -0,048204 | Нет | |
| 5,9919 | -0,032190 | Нет | |
| 5,9946 | -0,021484 | Да |
Уточненное по методу итераций значение корня: 5,9946.