Динамика сферического и свободного движения твердого тела.
По каким формулам вычисляются кинетические моменты твердого тела относительно неподвижной точки и относительно координатных осей при его сферическом движении?
Кинетический момент твердого тела, совершающего сферическое движение относительно неподвижной точки, определяется по общей формуле:
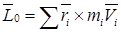 .
.
Кинетические моменты тела, совершающего сферическое движение, относительно координатных осей имеют вид:
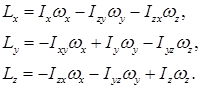
Чему равны кинетические моменты твердого тела относительно главных осей инерции, проведенных из неподвижной точки тела, при его сферическом движении?
Если за оси приняты главные оси инерции в неподвижной точке 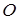 , то центробежные моменты инерции
, то центробежные моменты инерции 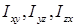 равны нулю и кинетические моменты относительно этих осей определяются по формулам:
равны нулю и кинетические моменты относительно этих осей определяются по формулам:
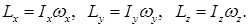
Какой вид имеют динамические уравнения Эйлера?
Динамические уравнения Эйлера имеют вид:
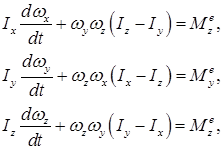
где 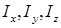 – моменты инерции тела относительно его осей инерции в точке О;
– моменты инерции тела относительно его осей инерции в точке О;
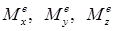 – главные моменты внешних сил, приложенных к телу, относительно этих же осей.
– главные моменты внешних сил, приложенных к телу, относительно этих же осей.
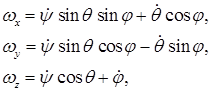
где 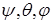 – углы Эйлера.
– углы Эйлера.
Какое твердое тело называют гироскопом?
Гироскопом называется тяжелое твердое тело, вращающееся вокруг оси материальной симметрии, одна из точек которой неподвижна.
Чему равен и как направлен кинетический момент быстровращающегося гироскопа относительно его неподвижной точки?
Кинетический момент гироскопа относительно неподвижной точки 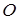 направлен вдоль оси симметрии гироскопа и равен
направлен вдоль оси симметрии гироскопа и равен
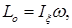
где 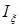 – момент инерции гироскопа.
– момент инерции гироскопа.
Какими физическими свойствами обладает быстровращающийся гироскоп с тремя степенями свободы?
Гироскоп с тремя степенями свободы обладает способностью противодействовать силам, стремящимся изменить направление его оси вращения.
Какой эффект производит действие одной и той же силы, приложенной к оси неподвижного и быстровращающегося гироскопа с тремя степенями свободы?
Под действием силы 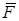 неподвижный гироскоп начинает вращаться вокруг оси, перпендикулярной плоскости, проходящей через линию действия силы
неподвижный гироскоп начинает вращаться вокруг оси, перпендикулярной плоскости, проходящей через линию действия силы 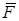 и неподвижную точку
и неподвижную точку 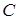 . После прекращения действия силы гироскоп продолжает вращаться по инерции вокруг этой оси с постоянной угловой скоростью, которую он приобрел под действием силы
. После прекращения действия силы гироскоп продолжает вращаться по инерции вокруг этой оси с постоянной угловой скоростью, которую он приобрел под действием силы 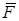 .
.
Под действием силы 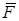 смещение оси гироскопа происходит не по направлению действия силы, а по направлению ее момента, перпендикулярно направлению силы.
смещение оси гироскопа происходит не по направлению действия силы, а по направлению ее момента, перпендикулярно направлению силы.
После прекращения действия силы гироскоп вращается вокруг своей оси симметрии, отклоненной от первоначального положения на угол 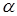 .
.
Выведите формулу для вычисления угловой скорости прецессии оси гироскопа.
Ось симметрии гироскопа вращается вокруг неподвижной оси 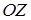 с некоторой угловой скоростью
с некоторой угловой скоростью 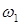 , описывая коническую поверхность. Это движение гироскопа называется регулярной прецессией, а угловая скорость
, описывая коническую поверхность. Это движение гироскопа называется регулярной прецессией, а угловая скорость 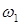 – угловой скоростью прецессии.
– угловой скоростью прецессии.
Угловая скорость прецессии 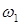 тем меньше, чем больше угловая скорость
тем меньше, чем больше угловая скорость 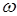 вращения гигроскопа вокруг его оси симметрии.
вращения гигроскопа вокруг его оси симметрии.
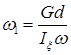 .
.
В чем состоит разница в свойствах гироскопов с двумя и тремя степенями свободы?
Гироскоп с двумя степенями свободы не обладает способностью противодействовать изменению направления его оси вращения.
Какова физическая сущность гироскопического эффекта и при каких условиях он наблюдается?
Гироскопический момент МГ представляет собой момент пары, составленной силами инерции гироскопа и равен по величине
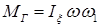 .
.
Гироскопический эффект проявляется всегда, когда изменяется направление оси быстровращающегося гироскопа.
По каким формулам определяются динамические реакции подшипников, в которых вращается рама вращающегося гироскопа с двумя степенями свободы?
Динамические реакции подшипников равны по величине
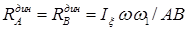 .
.
Каковы дифференциальные уравнения движения свободного твердого тела?
Шесть дифференциальных уравнений движения свободного твердого тела имеют вид:
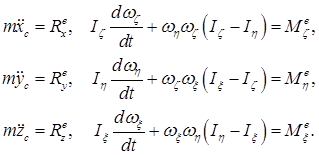
При каких условиях движение свободного твердого тела является поступательным?
Для поступательного движения твердого тела необходимо, чтобы в начальный момент движения кинетический момент тела относительно центра масс был равен нулю и главный момент внешних сил относительно центра масс тела все время оставался равным нулю.
