Теорема об изменении кинетической энергии.

Каковы две меры механического движения и соответствующие им измерители действия силы?

В механике рассматривается два случая преобразования механического движения:

· механическое движение переносится с одной системы на другую в качестве механического движения (количество движения). Мерой движения силы в этом случае является вектор импульса силы .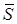

· механическое движение превращается в другую форму движения (потенциальной энергии, теплоты и т. д.). В качестве меры механического движения выступает кинетическая энергия. Мерой действия силы в этом случае является работа.

Как определяется работа постоянной по модулю и направлению силы на прямолинейном перемещении?

Работа постоянной силы равна произведению модуля силы на длину пути, пройденного точкой приложения силы и на косинус угла между направлениями вектора силы и вектора перемещения точки ее приложения.

.

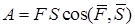Чему равна работа силы трения скольжения, если эта сила постоянна по модулю и направлению?

Работа постоянной силы трения скольжения равна .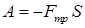

Каким простым способом можно вычислить работу постоянной по модулю и направлению силы на криволинейном перемещении?

При вычислении работы силы на криволинейном перемещении криволинейное перемещение можно заменить прямолинейным и определить работу по формуле

.

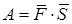Чему равна работа равнодействующей силы?

Работа равнодействующей силы на некотором перемещении равна алгебраической сумме работ составляющих сил на том же перемещении

.

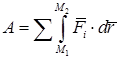Как выразить элементарную работу силы через элементарный путь точки приложения силы и как — через приращение дуговой координаты этой точки?

Элементарная работа силы 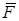на участке 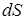определяется по формуле

.

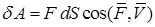Работу на перемещении 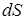совершает только касательная составляющая силы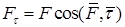

.

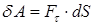Каково векторное выражение элементарной работы?

Элементарную работу силы 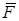на элементарном перемещении 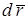можно представить как скалярное произведение .

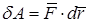Каково выражение элементарной работы силы через проекции силы на оси координат?

Элементарная работа силы 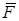на перемещении 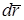через проекции 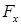, , 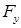, , 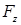, 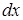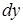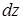может быть представлена в виде

.

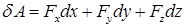Напишите различные виды криволинейного интеграла, определяющего работу переменной силы на конечном криволинейном перемещении.

, , ,

, .

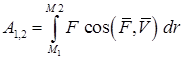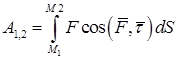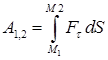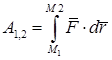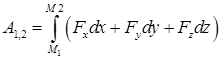В чем состоит графический способ определения работы переменной силы на криволинейном перемещении?

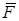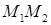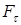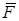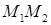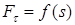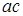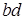Для графического определения работы силы на перемещении по оси абсцисс откладываются значения дуговой координаты точки S, а по оси ординат – соответствующие значения проекции силы на касательную . Работа силы на перемещении изобразиться площадью фигуры, ограниченной осью абсцисс, кривой и ординатами и , соответствующими точкам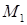и и .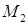

Как вычисляются работа силы тяжести и работа силы упругости?

Работа силы тяжести равна взятому со знаком плюс или минус произведению силы тяжести на вертикальное перемещение точки ее приложения. Работа силы тяжести не зависит от вида траектории. Работа силы упругости определяется по формуле

,

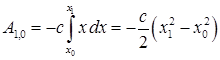где 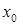— начальная деформация.

На каких перемещениях работа силы тяжести: а) положительна, б) отрицательна, в) равна нулю?

Работа силы тяжести на перемещении :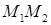

а) положительна, если точка 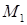расположена выше точки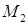

б) отрицательна, если точка 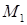расположена ниже точки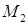

,

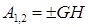где знак плюс соответствует перемещению точки вниз, а знак минус – перемещению точки вверх.

В каком случае работа силы упругости положительна и в каком — отрицательна?

Работа силы упругости отрицательна в том случае, когда деформация увеличивается, т. е. когда сила упругости направлена противоположно перемещению ее точки приложения, и положительна, когда деформация уменьшается.

Сформулируйте теорему об изменении кинетической энергии материальной точки.

Дифференциал кинетической энергии материальной точки равен сумме элементарных работ, приложенных к точке сил

.

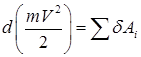Изменение кинетической энергии точки на некотором ее перемещении равно алгебраической сумме работ всех действующих на эту точку сил на этом же перемещении

.

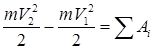Сформулируйте теорему об изменении кинетической энергии материальной точки в относительном движении. Почему равна нулю работа кориолисовой силы инерции?

Выражение теоремы об изменение кинетической энергии для относительного движения точки имеет вид

.

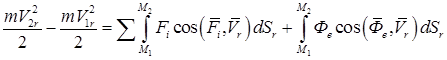Сила инерции Кориолиса 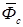всегда перпендикулярна относительной скорости точки 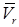. Следовательно, работа силы инерции Кориолиса на относительном перемещении точки равна нулю.

Какова сумма работ внутренних сил твердого тела на любом перемещении тела?

Т. к. каждой внутренней силе соответствует другая, равная ей по модулю и противоположная по направлению, то сумма элементарных работ всех внутренних сил равна нулю.

Как вычисляется сумма элементарных работ внешних сил, приложенных к твердому телу: а) в случае поступательного движения; б) в случае его вращения вокруг неподвижной оси и в) в общем случае его движения?

Элементарная работа сил, приложенных к твердому телу, движущемуся поступательно, равна элементарной работе главного вектора внешних сил, приложенного в любой точке тела

.

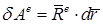Элементарная работа сил, приложенных к твердому телу, вращающемуся вокруг неподвижной оси, равна произведению главного момента внешних сил относительно оси вращения на приращение угла поворота

.

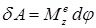Элементарная работа внешних сил, приложенных к свободному твердому телу в общем случае его движения, равна сумме элементарных работ их главного вектора на перемещение точки его приложения и главного момента этих сил относительно мгновенной оси, проходящей через полюс, на перемещение при повороте вокруг этой оси

.

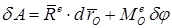Как вычисляется мощность сил, приложенных к твердому телу, вращающемуся вокруг неподвижной оси с угловой скоростью ?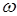

Изменение работы за единицу времени называется мощностью силы

.

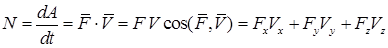Если твердое тело вращается вокруг неподвижной оси с угловой скоростью 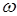то мощность сил определяется по формуле

.

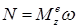Что представляет собой сопротивление качению? Что называется коэффициентом трения качения и какова его размерность?

При качении цилиндрического катка по не абсолютно твердой поверхности происходит деформация соприкасающихся поверхностей и линия действия нормальной реакции оказывается сдвинутой в сторону движения катка на некоторое расстояние 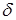от линии действия силы веса 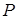. Реакция плоскости N и вес 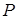образуют пару сил сопротивления с плечом 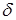. Момент этой пары называется моментом сопротивления качению

.

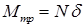Коэффициент трения качения 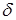имеет размерность длины.

Сформулируйте теорему Кенига о кинетической энергии механической системы в общем случае ее движения.

Кинетическая энергия механической системы равна сумме кинетической энергии центра масс системы, масса которого равна массе всей системы, и кинетической энергии этой системы в ее движении относительно центра масс

.

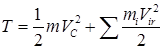Как вычисляется кинетическая энергия твердого тела в различных случаях его движения?

Кинетическая энергия поступательно движущегося тела равна половине произведения массы тела на квадрат его скорости

.

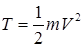Кинетическая энергия твердого тела, вращающегося вокруг неподвижной оси, равна половине произведения его момента инерции относительно оси вращения на квадрат угловой скорости тела

.

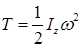При плоском движении твердого тела кинетическая энергия равна сумме кинетической энергии в поступательном движении вместе с центром масс и кинетической энергии во вращении тела относительно подвижной оси, проходящей через центр масс

.

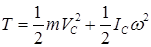Кинетическая энергия твердого тела, совершающего сферическое движение равна половине произведения момента инерции тела относительно мгновенной оси вращения на квадрат угловой скорости тела

.

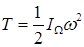При этом значение момента инерции 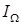непрерывно изменяется. Кинетическая энергия твердого тела в общем случае его движения равна сумме кинетической энергии тела, в его переносном поступательном движении вместе с центром масс и сферическом движении относительно центра масс

.

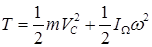Сформулируйте теорему об изменении кинетической энергии механической системы.

Дифференциал кинетической энергии механической системы равен сумме элементарных работ внешних 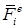и внутренних сил 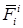системы

.

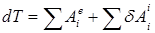Производная по времени от кинетической энергии системы равна сумме мощностей внешних и внутренних сил системы

.

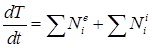Изменение кинетической энергии системы на некотором перемещении равно сумме работ внешних и внутренних сил, действующих на систему

.

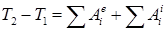Потенциальное силовое поле.

Какое силовое поле называется потенциальным?

Стационарное силовое поле называют потенциальным, если существует такая функция, однозначно зависящая от координат точек системы, через которую проекции силы на координатные оси в каждой точке поля выражаются так:

, , .

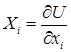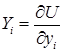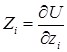Что называется силовой функцией?

Функцию 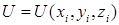, где 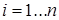называют силовой функцией.

Как определить элементарную работу сил потенциального поля и работу этих сил на конечном перемещении системы, если известна силовая функция поля?

Если силовое поле является потенциальным, элементарная работа сил в этом поле равна полному дифференциалу силовой функции.

.

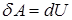Какова работа сил, действующих на точки системы в потенциальном поле, на замкнутом перемещении?

Работа сил, действующих на точки механической системы в потенциальном поле, равна разности значений силовой функции в конечном и начальном положении и не зависит от формы траектории точки

.

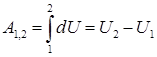Работа сил, действующих на точки механической системы в потенциальном поле на всяком замкнутом перемещении равна нулю, т. к. .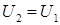

Чему равна потенциальная энергия системы в любом ее положении?

Потенциальная энергия системы в любом данном ее положении равна сумме работ сил потенциального поля, приложенные к ее точкам на перемещении системы из данного положения в нулевое

.

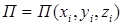Чему равно изменение потенциальной энергии механической системы при перемещении ее из одного положения в другое?

Изменение потенциальной энергии механической системы при перемещении ее из одного положения в другое равно работе сил, приложенных к точкам системы, на том же перемещении

.

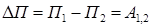Какая зависимость существует между силовой функцией потенциального поля и потенциальной энергией системы, находящейся в этом поле?

Потенциальная энергия системы 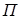отличается от силовой функции 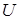, взятой со знаком минус, на постоянную величину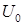

.

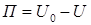Как определяются проекции на координатные оси силы, действующей в потенциальном поле на любую точку системы?

Проекции на координатные оси силы, действующей в потенциальном поле на каждую точку системы, равны взятым со знаком минус частным производным от потенциальной энергии системы по соответствующим координатам этой точки

, , .

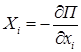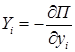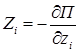Какие поверхности называются эквипотенциальными и каковы их уравнения?

Геометрическое место точек пространства, в которых потенциальная энергия имеет одно и то же значение называется поверхностью равного потенциала или эквивалентной поверхностью и определяется уравнением

.

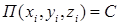Как направлена сила, действующая на материальную точку в потенциальном поле, по отношению к эквипотенциальной поверхности, проходящей через эту точку?

Сила 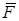направлена по нормали к эквипотенциальной поверхности, проходящей через данную точку в сторону уменьшения значений потенциальной энергии.

Чему равна потенциальная энергия материальной точки и механической системы, находящихся под действием сил тяжести?

Потенциальная энергия материальной точки, находящейся под действием силы тяжести, равна

.

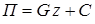Потенциальная энергия механической системы, находящейся под действием силы тяжести, равна произведению веса системы на высоту ее центра масс над нулевой эквипотенциальной поверхностью

.

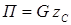Какой вид имеют эквипотенциальные поверхности поля силы тяжести и ньютоновой силы тяготения?

Эквипотенциальные поверхности поля силы тяжести представляют собой горизонтальные плоскости. Сила тяжести направлена перпендикулярно этим плоскостям в сторону уменьшения значений потенциальной энергии.

Эквипотенциальные поверхности поля силы притяжения представляют собой сферические поверхности с центром в точке O. Уравнение эквипотенциальных поверхностей имеет вид

.

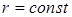В чем заключается закон сохранения и превращения механической энергии?

При движении механической системы в стационарном потенциальном поле полная механическая энергия системы при движении остается постоянной.

.

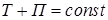Почему под действием центральной силы материальная точка описывает плоскую кривую?

Если материальная точка движется под действием центральной силы, то момент количества движения точки относительно центра постоянен и точка движется в плоскости перпендикулярной вектору .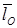

Что называют секторной скоростью и как выразить ее модуль в полярных координатах?

Величина 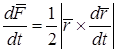называется секторной скоростью.

В чем заключается закон площадей?

При движении точки под действием центральной силы площадь, описывается радиусом — вектором точки, изменяется пропорционально времени

.

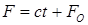Какой вид имеет дифференциальное уравнение в форме Бине, определяющее траекторию точки, движущейся под действием центральной силы?

Уравнение движения точки в форме Бине: .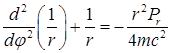

В случае притяжения, когда 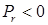, траектория обращена к полюсу O вогнутостью.

Принцип Даламбера.

В чем заключается сущность принципа Германа — Эйлера — Даламбера для материальной точки?

Геометрическая сумма всех приложенных к точке сил и силы инерции этой точки равны нулю.

.

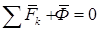Каким условиям удовлетворяют в любой момент времени главные векторы внешних задаваемых сил, реакций связей и сил инерции точек несвободной механической системы и главные моменты этих сил относительно любого неподвижного центра?

В любой момент времени геометрическая сумма главных векторов задаваемых сил, реакций связей и сил инерции точек системы равны нулю.

В любой момент времени для всякой несвободной механической системы геометрическая сумма главных моментов задаваемых сил, реакций связей и сил инерции относительно любого неподвижного центра равна нулю.

Каковы модуль и направление главного вектора сил инерции механической системы?

Главный вектор сил инерции равен:

.

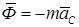Модуль главного вектора сил инерции

.

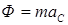К чему приводятся силы инерции точек твердого тела:

а) при поступательном движении тела;

при поступательном движении силы инерции приводятся к равнодействующей силе, приложенной в центре масс тела, равной по модулю произведению массы тела на модуль ускорения его центра масс и направлены противоположно этому ускорению;

б) при вращении тела, имеющего плоскость материальной симметрии, вокруг неподвижной оси, перпендикулярной этой плоскости;

при вращении твердого тела, имеющего плоскость материальной симметрии, вокруг оси перпендикулярной этой плоскости, силы инерции приводятся к равнодействующей силе, лежащей в плоскости симметрии. Модуль и направление этой силы равны главному вектору сил инерции, а расстояние от ее линии действия до точки пересечения оси вращения с плоскостью симметрии равно

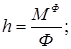
в) при плоском движении тела, имеющего плоскость материальной симметрии?

Если твердое тело, имеющее плоскость материальной симметрии, движется параллельно этой плоскости, то силы инерции приводятся к силе, приложенной в центре масс и равной главному вектору сил инерции 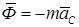, и к паре сил, лежащей в плоскости симметрии, числовое значение момента которой определяется формулой:

.

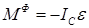При каких условиях динамические давления вращающегося тела на опоры равны нулю?

Динамические составляющие реакций подшипников равны нулю в том случае, если ось вращения тела является главной центральной осью инерции тела.