Замкнутость реляционной алгебры

Реляционная алгебра представляет собой набор таких операций над отношениями, что результат каждой из операций также является отношением. Это свойство алгебры называется замкнутостью.

Операции над одним отношением называются унарными, над двумя отношениями — бинарными, над тремя — тернарными (таковые практически неизвестны).

Пример унарной операции — проекция, пример бинарной операции — объединение.

N-арную реляционную операцию f можно представить функцией, возвращающей отношение и имеющей n отношений в качестве аргументов:

{\displaystyle R=f(R_{1},R_{2},\dots ,R_{n})}

Поскольку реляционная алгебра является замкнутой, в качестве операндов в реляционные операции можно подставлять другие выражения реляционной алгебры (подходящие по типу):

{\displaystyle R=f(f_{1}(R_{11},R_{12},\dots ),f_{2}(R_{21},R_{22},\dots ),\dots )}

В реляционных выражениях можно использовать вложенные выражения сколь угодно сложной структуры.

Ограничения на операции[править | править вики-текст]

Некоторые реляционные операции, в частности, операции объединения, пересечения и вычитания, требуют, чтобы отношения имели совпадающие (одинаковые) заголовки (схемы). Это означает, что совпадают количество атрибутов, названия атрибутов и тип (домен) одноимённых атрибутов.

Некоторые отношения формально не являются совместимыми из-за различия в названиях атрибутов, но становятся таковыми после применения операции переименования атрибутов.

Операции реляционной алгебры[править | править вики-текст]

Далее перечислены некоторые операции реляционной алгебры, которые представляют либо исторический, либо практический интерес. Все операции перечислить невозможно, поскольку любая операция, удовлетворяющая определению реляционной, является частью реляционной алгебры.

Переименование[править | править вики-текст]

Результатом применения операции переименования атрибутов является отношение с изменёнными именами атрибутов.

Синтаксис:

R RENAME Atr₁, Atr₂, … AS NewAtr₁, NewAtr₂, …

где

R — отношение

Atr₁, Atr₂, … — исходные имена атрибутов

NewAtr₁, NewAtr₂, … — новые имена атрибутов.

Объединение[править | править вики-текст]

Отношение с тем же заголовком, что и у совместимых по типу отношений A и B, и телом, состоящим из кортежей, принадлежащих или A, или B, или обоим отношениям.
Синтаксис:

A UNION B

Пересечение[править | править вики-текст]

Отношение с тем же заголовком, что и у отношений A и B, и телом, состоящим из кортежей, принадлежащих одновременно обоим отношениям A и B.
Синтаксис:

A INTERSECT B

Вычитание[править | править вики-текст]

Отношение с тем же заголовком, что и у совместимых по типу отношений A и B, и телом, состоящим из кортежей, принадлежащих отношению A и не принадлежащих отношению B.
Синтаксис:

A MINUS B

Декартово произведение[править | править вики-текст]

Отношение (A₁, A₂, …, A_m, B₁, B₂, …, B_m), заголовок которого является сцеплением заголовков отношений A(A₁, A₂, …, A_m) и B(B₁, B₂, …, B_m), а тело состоит из кортежей, являющихся сцеплением кортежей отношений A и B:

(a₁, a₂, …, a_m, b₁, b₂, …, b_m)

таких, что

(a₁, a₂, …, a_m)∈ A,

(b₁, b₂, …, b_m)∈ B.

Синтаксис:

A TIMES B

Выборка (ограничение)[править | править вики-текст]

Отношение с тем же заголовком, что и у отношения A, и телом, состоящим из кортежей, значения атрибутов которых при подстановке в условие c дают значение ИСТИНА. c представляет собой логическое выражение, в которое могут входить атрибуты отношения A и/или скалярные выражения.
Синтаксис:

A WHERE c

Проекция[править | править вики-текст]

Основная статья: Проекция (реляционная алгебра)

При выполнении проекции выделяется «вертикальная» вырезка отношения-операнда с естественным уничтожением потенциально возникающих кортежей-дубликатов.
Синтаксис:

A[X, Y, …, Z]

или

PROJECT A {x, y, …, z}

Соединение[править | править вики-текст]

Операция соединения отношений A и B по предикату P логически эквивалентна последовательному применению операций декартового произведения A и B и выборки по предикату P. Если в отношениях имеются атрибуты с одинаковыми наименованиями, то перед выполнением соединения такие атрибуты необходимо переименовать.

Синтаксис:

(A TIMES B) WHERE P

Деление[править | править вики-текст]

Отношение с заголовком (X₁, X₂, …, X_n) и телом, содержащим множество кортежей (x₁, x₂, …, x_n), таких, что для всех кортежей (y₁, y₂, …, y_m) ∈ B в отношении A(X₁, X₂, …, X_n, Y₁, Y₂, …, Y_m) найдется кортеж (x₁, x₂, …, x_n, y₁, y₂, …, y_m).
Синтаксис:

A DIVIDEBY B

9. Теоретико-множественные операции.

Теоретико-множественные операции реляционной алгебры – это операции, привнесенные в реляционную алгебру из теории множеств.

Выделяют следующие теоретико-множественные операции:

· объединение;

· пересечение;

· разность;

· расширенное декартово произведение.

Объединением двух отношений называется отношение, содержащее множество кортежей, принадлежащих либо первому, либо второму исходному отношению, либо обоим отношениям одновременно.

Пусть заданы два отношения 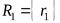, , 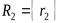гдеr₁ и r₂ - соответственно кортежи отношений R₁ и R₂, тогда объединение

,

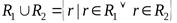где r – кортеж нового отношения; 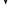- операция логического «ИЛИ».

Рассмотрим пример данной операции.

Предположим, имеются отношения R₁ и R₂, которые содержат списки деталей, изготавливаемых соответственно на первом и втором участках цеха. Отношение R₃ содержит общий перечень деталей, изготавливаемых в цехе.

Пересечением отношений называется отношение, которое содержит множество кортежей, принадлежащих одновременно и первому и второму отношениям.

,

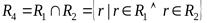где r – кортеж нового отношения; 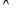- операция логического «И».

В отношении R₄ содержится перечень деталей, которые выпускаются одновременно на двух участках цеха.

Разностью отношений R₁ и R₂ называется отношение, содержащее множество кортежей, принадлежащих R₁ и не принадлежащих R₂.

R₅ содержит перечень деталей, изготавливаемых только на участке 1, отношение R₆ – только на участке 2.

,

.

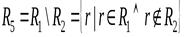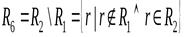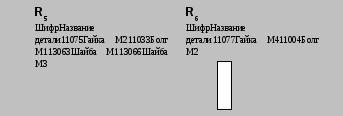
Операции объединения и пересечения являются коммутативными, т.е. результат этих операций не зависит от порядка следования аргументов в операции.

Операция разности является несимметричной, т.е. результат операции будет различным для различного порядка аргументов.

В отличие от навигационных средств манипулирования данными, в теоретико-графовых моделях операции реляционной алгебры позволяют получить качественно иной результат:

1. Операции сразу целиком выполняются на отношениях.

Для пользователя и прикладного программиста это означает, что в результате таких операций он сразу получит результат. Следовательно, пользователю не придется «вручную» последовательно перемещаться по базе данных в поисках необходимых записей, а программисту не придется писать отдельную программу для простейшей обработки данных;

2. Результатом выполнения операции является новое отношение, отражающее состояние исходного отношения в определенной части.

Расширенное декартово произведение– это операция, сходная с полным декартовым произведением множеств. В полном декартовом произведении участвуют домены, т.е. полное декартово произведение множеств – это сцепление всех возможных значений доменов друг с другом в определенном порядке. Расширенное декартово произведение – это сцепление реальных множеств, реальных наборов атрибутов отношения друг с другом.

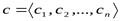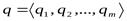Сцеплением или конкатенацией кортежей и называется кортеж, полученный добавлением значений второго в конец первого. Сцепление кортеже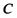й и 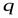обозначается как .

,

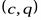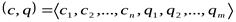где 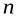– число элементов в первом кортеже, 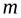– число элементов во втором кортеже.

Расширенным декартовым произведением отношения 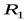степени 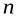со схемой 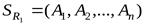и отношения 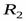степени 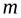со схемой 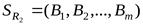называется отношение 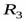степени 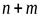со схемой 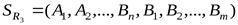, содержащее кортежи, полученные сцеплением каждого кортежа 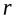отношения 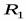с каждым кортежем 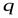отношения .

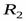Т.е. если 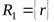, , 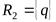то

.

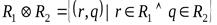Операцию расширенного декартова произведения можно считать симметричной ( 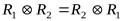), т.к. полученные отношения эквивалентны.

Операция расширенного декартова произведения используется для получения некоторого универсума – отношения, которое характеризует все возможные комбинации между элементами отдельных множеств.

Например, пусть существует отношение 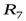, содержащее обязательную номенклатуру деталей для всех цехов, и отношение 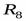, содержащее перечень всех цехов. Требуется получить отношение, в котором была бы отражена ситуация, когда каждый цех изготавливаетвседетали.

Универсум не имеет самостоятельного значения, но может активно использоваться в операциях над данными. Так, операцию расширенного декартова произведения (или получения универсума) нужно использовать во всех ситуациях, которые характеризуются словом «все».

Например, нужно узнать, какие детали в каких цехах из общей обязательной номенклатуры не выпускаются ( 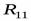). В данном случае универсумом является общая обязательная номенклатура ( 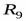). Имеется также отношение 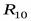, характеризующее реальный выпуск деталей в каждом цехе. Для получения искомого результата необходимо выполнить следующую операцию:

.

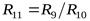10. Специальные операции реляционной алгебры.

11. Типы данных SQL Server.

bigint	Целочисленные данные (целые числа) от –2^63 (–9 223 372 036 854 775 808) до 2^63–1 (9 223 372 036 854 775 807). Размер хранения составляет 8 байт.
integer	Целочисленные данные (целые числа) от –2^31 (–2 147 483 648) до 2^31–1 (2 147 483 647). Размер хранения составляет 4 байта.
smallint	Целочисленные данные от –32 768 до 32 767. Размер хранения составляет 2 байта.
tinyint	Целочисленные данные от 0 до 255. Размер занимаемой памяти — 1 байт.
bit	Целочисленные данные со значением 1 либо 0. Размер занимаемой памяти — 1 бит.
numeric (p, s) Synonyms: decimal(p,s) and dec (p,s)	Данные с фиксированной точностью и численным масштабом от –10^38+1 до 10^38–1. Переменная p указывает точность и может принимать значения от 1 до 38. Переменная s указывает масштаб, она может принимать значения от 0 до p. Размер хранения составляет 19 байт.
money	Значения денежных данных от (–2^63/10000) (–922 337 203 685 477,5808) до 2^63–1 (922 337 203 685 477,5807) с точностью до десятитысячной доли денежной единицы. Размер хранения составляет 8 байт.
float	Числовые данные с плавающей запятой от –1,79E +308 до 1,79E+308 Размер хранения составляет 8 байт.
real	Числовые данные с плавающей точностью от –3.40E+38 до 3.40E+38. Размер хранения составляет 4 байта.
datetime	Данные даты и времени от 1 января 1753 г. по 31 декабря 9999 г. с точностью до одной трехсотой секунды или 3,33 миллисекунды. Значения округляются с шагом 0,000, 0,003 или 0,007 миллисекунд. Хранятся как два 4-байтовых целочисленных значения. В первых 4 байтах хранится количество дней до или после base date, 1 января 1900 г. Базовая дата — это эталонная дата системы. Значения для datetime ранее 1 января 1753 г. запрещены. В других 4 байтах хранится время дня в миллисекундах после полуночи. Допустимый диапазон секунд — от 0 до 59. ФорматПример ГГГГ-ММ-ДД чч:мм:сс1947/08/15 03:33:20 ММ-ДД-ГГГГ чч:мм:сс04/15/1947 03:33:20 ДД ГГГГ ММ чч:мм:сс15 янв 1947 03:33:20 ДД ММММ ГГГГ ч:мм:сс15 января 1947 03:33:20
national character(n) Synonym:nchar(n)	Данные Юникод постоянной длины с максимальной длиной 4 000 символов. Стандартная длина = 1. Размер занимаемой памяти в байтах — количество введенных символов, умноженное на два.
national character varying(n) Synonym:nvarchar(n)	Данные Юникод переменной длины с максимальной длиной от 1 до 4 000 символов. Стандартная длина = 1. Размер занимаемой памяти в байтах — количество введенных символов, умноженное на два.
ntext¹	Данные Юникод переменной длины с максимальной длиной (2^30–2)/2 (536,870,911) символов. Размер занимаемой памяти в байтах — количество введенных символов, умноженное на два. Примечание В строковых функциях ntext более не поддерживается.
nchar	Данные в Юникоде постоянной длины n знаков, значение n должно быть в диапазоне от 1 до 4 000. Занимаемый размер — 2n байт.
binary(n)	Двоичные данные Юникод постоянной длины с максимальной длиной 8 000 байт. Стандартная длина = 1. Размер занимаемой памяти не изменяется, его длина в байтах заявлена в типе.
varbinary(n)	Двоичные данные Юникод переменной длины с максимальной длиной 8 000 байт. Стандартная длина = 1. Размер занимаемой памяти изменяется. Он равен длине значения в байтах.
image¹	Двоичные данные Юникод переменной длины с максимальной длиной 2^30–1 (1 073 741 823) байт. Хранилище данных — это длина значения в байтах.
uniqueidentifier	Глобальный уникальный идентификатор (GUID). Размер занимаемой памяти — 16 байт.
IDENTITY [(s, i)]	Это свойство столбца данных, где содержатся данные неопределенного типа. Для столбцов удостоверений могут быть использованы только столбцы целочисленных данных. В таблице может содержаться только один столбец идентификаторов. Если указать начальное значение и значение шага, столбец будет невозможно обновить. s (seed) = начальное значение i(increment) = значение шага
ROWGUIDCOL	Это свойство столбца данных, где содержатся данные неопределенного типа. Это столбец таблицы, который определен с помощью типа данных uniqueidentifier. В таблице может содержаться только один столбец ROWGUIDCOL.
Timestamp/rowversion	Это автоматически создаваемый уникальный двоичный номер. Размер занимаемой памяти — 8 байт.

· Binary(до 1.2 ГБ) - поля данного типа позволяют хранить любые данные в двоичном формате.

· Varbinary

· Tinyint(1 байт) - хранит целое число 0-255.

· Char - 1 байт на символ, позволяет хранить строку до 254 символов длинной для одного поля.

· Varchar

· Money(8 байт) - Число с обозначением денежной единицы.

· Date and time(8 байт) - Дата и время с точностью в 3.33 милисекунды.

· Smalldatetime(4 байта) - Дата и время с точностью в 1 секунду.

· Bit(1 байт) - Два значения TRUE или FALSE.

· Float(1-20 байт) - Дробные и целые числа со знаком.

· Smallint(2 байта) - Целое число от -32768 до +32767.

· Int(4 байта) - Целое число от -2147483647 до 2147483646.

· Image(4 байта) - Ссылка на OLE.

· Text(4 байта) - Примечание на блок данных.

· Decimal(p,s) точное число p знаков до запятой ( не больше 38) s после запятой не больше p

· numeric(p,s) точное число p знаков до запятой ( не больше 38) s после запятой не больше p

· real(4 байта) - Интервал от 1.401298E-45 до 3.403823E38.

12. Структура языка SQL.