Выборочными уравнениями регрессии.

Статистической гипотезой (или просто гипотезой) называется всякое предположение о виде распределения изучаемого признака или о неизвестных параметрах известного распределения изучаемого признака.

Выдвинутую гипотезу 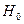называют нулевой или основной

Конкурирующей или альтернативной называют гипотезу 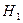, которая противоречит основной гипотезе.

Гипотезу, содержащую только одно предположение, называют простой,

в противном случае - сложной.

При стат. проверке стат. гипотезы могут быть допущены ошибки двух родов:

Ошибка первого родасостоит в том, что отвергается нулевая гипотеза, когда она на самом деле верна. Ошибка второго рода состоит в том, что отвергается альтернативная гипотеза, когда она на самом деле верна.

Вероятность ошибки первого рода называется уровнем значимости и обозначается через .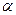

Специально подобранная случайная величина K , которая служит для проверки нулевой гипотезы,

наз. статистическим критериемили просто критерием.

Наблюдаемое значение статистического критерия 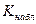- это значение стат. критерия, вычисленное по произведённой выборке.

Критическая область- это множество возможных значений стат. критерия, при которых нулевая гипотеза отвергается.

Область принятия гипотезы– это множество возможных значений стат. критерия , при которых нулевая гипотеза принимается.

Критические точки 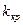, или квантили - это точки, которые разграничивают критическую область и область принятия гипотезы.

Правосторонняя критическая областьопределяется неравенством K> 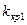>0 .

Левосторонняя критическая область определяется неравенством K< 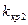<0 .

Двусторонняя критическая область определяется совокупностью указанных выше неравенств.

Критерием согласия наз. стат. критерий проверки гипотезы о предполагаемом законе распределения изучаемого признака генеральной совокупности.

РАЗДЕЛ 5. Практикум по решению задач по темам лекций.

Примеры решения задач.

Пример 1. Найти вероятность того, что точка, наудачу брошенная в круг, не попадет в правильный шестиугольник, вписанный в него.

Решение. Пусть радиус круга равен R , тогда сторона шестиугольника тоже равна R. При этом площадь круга 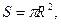а площадь шестиугольника 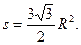Следовательно,

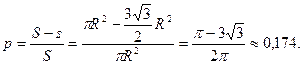
Пример 2. На отрезок АВ случайным образом брошены три точки: С, D и М. Найти вероятность того, что из отрезков АС, АD и АМ можно построить треугольник.

Решение. Обозначим длины отрезков АС, АD и АМ через x, y и z и рассмотрим в качестве возможных исходов множество точек трехмерного пространства с координатами (х, у, z). Если принять длину отрезка равной 1, то эти множество возможных исходов представляет собой куб с ребром, равным 1. Тогда множество благоприятных исходов состоит из точек, для координат которых выполнены неравенства треугольника: x + y > z, x + z > y, y + z > x. Это часть куба, отрезанная от него плоскостями x + y = z, x + z = y, y + z = x

хРис.1.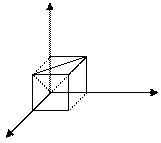

(одна из них, плоскость x + y = z, проведена на рис.1). Каждая такая плоскость отделяет от куба пирамиду, объем которой равен 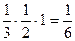. Следовательно, объем оставшейся части

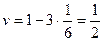. Тогда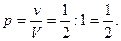

Пример 3. Из урны, содержащей 2 белых и 6 черных шаров, случайным образом извлекаются 5 шаров. Найти вероятность того, что вынуты шары разных цветов.

Решение. Событие 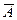, противоположное заданному, заключается в том, что из урны вынуто 5 шаров одного цвета, а так как белых шаров в ней всего два, то этот цвет может быть только черным. Множество возможных исходов опыта найдем по формуле (1.5):

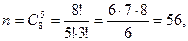
а множество исходов, благоприятных событию 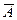- это число возможных наборов по 5 шаров только из шести черных:

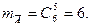
Тогд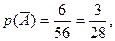а а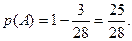

Пример 4. Пусть событие А – извлечение из колоды в 32 карты туза, а событие В – то, что и вторая вынутая из колоды карта окажется тузом. Тогда, если после первого раза карта была возвращена в колоду, то вероятность вынуть вторично туз не меняется: 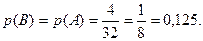Если же первая карта в колоду не возвращается, то осуществление события А приводит к тому, что в колоде осталась 31 карта, из которых только 3 туза. Поэтому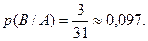

Пример 5. Для поражения цели необходимо попасть в нее дважды. Вероятность первого попадания равна 0,2, затем она не меняется при промахах, но после первого попадания увеличивается вдвое. Найти вероятность того, что цель будет поражена первыми двумя выстрелами.

Решение. Пусть событие А – попадание при первом выстреле, а событие В – попадание при втором. Тогда р (А) = 0,2, р (В/А) = 0,4, р (АВ) = 0,2·0,4 = 0,08.

Пример 6. Два стрелка делают по одному выстрелу по мишени. Вероятности их попадания при одном выстреле равны соответственно 0,6 и 0,7. Найти вероятности следующих событий:

А – хотя бы одно попадание при двух выстрелах;

В – ровно одно попадание при двух выстрелах;

С – два попадания;

D – ни одного попадания.

Решение. Пусть событие Н₁ – попадание первого стрелка, Н₂ – попадание второго. Тогда

А = Н₁ + Н₂, В =Н₁ 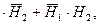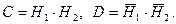События Н₁ и Н₂ совместны и независимы, поэтому теорема сложения применяется в общем виде, а теорема умножения – в виде (2.8). Следовательно, р(С) = 0,6·0,7 = 0,42, р(А) = 0,6 + 0,7 – 0,42 = 0,88,

р(B) = 0,6·0,3 + 0,7·0,4 = 0,46 (так как события 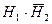и 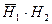несовместны),

р(D) = 0,4·0,3 = 0,12. Заметим, что события А и D являются противоположными, поэтому

р(А) = 1 – р(D).

Пример 7. Имеются три одинаковые урны с шарами. В первой из них 3 белых и 4 черных шара, во второй – 2 белых и 5 черных, в третьей – 10 черных шаров. Из случайно выбранной урны наудачу вынут шар. Найти вероятность того, что он белый.

Решение. Будем считать гипотезами Н₁, Н₂ и Н₃ выбор урны с соответствующим номером. Так как по условию задачи все гипотезы равновозможны, то 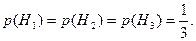Найдем условную вероятность А при реализации каждой гипотезы: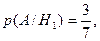

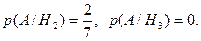Тогда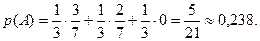

Пример 8. После двух выстрелов двух стрелков, вероятности попаданий которых равны 0,6 и 0,7, в мишени оказалась одна пробоина. Найти вероятность того, что попал первый стрелок.

Решение. Пусть событие А – одно попадание при двух выстрелах, а гипотезы: Н₁ – первый попал, а второй промахнулся, Н₂ – первый промахнулся, а второй попал, Н₃ – оба попали, Н₄ – оба промахнулись. Вероятности гипотез: р(Н₁) = 0,6·0,3 = 0,18, р(Н₂) = 0,4·0,7 = 0,28, р(Н₃) = 0,6·0,7 = 0,42, р(Н₄) = 0,4·0,3 = 0,12.Тогда р(А/Н₁) = р(А/Н₂) = 1, р(А/Н₃) = р(А/Н₄) = 0. Следовательно, полная вероятность р(А) = 0,18·1 + 0,28·1 + 0,42·0 + 0,12·0 = 0,46. Применяя формулу Байеса, получим:

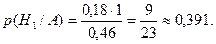
Пример 9 .При проведении 20 серий из 10 бросков игральной кости число выпадений шести очков оказалось равным 1,1,4,0,1,2,1,2,2,0,5,3,3,1,0,2,2,3,4,1.Составим вариационный ряд: 0,1,2,3,4,5. Статистический ряд для абсолютных и относительных частот имеет вид:

xi
ni
wi	0,15	0,3	0,25	0,15	0,1	0,05

Пример 10. Найдем числовые характеристики выборки, заданной статистическим рядом

xi
ni

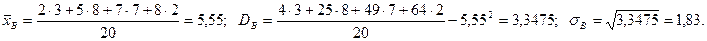Другими характеристиками вариационного ряда являются:

- мода М₀ – варианта, имеющая наибольшую частоту (в предыдущем примере М₀ = 5 ).

- медиана т_е - варианта, которая делит вариационный ряд на две части, равные по числу вариант. Если число вариант нечетно ( n = 2k + 1 ), то m_e = x_k+1, а при четном n =2k 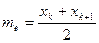. В частности, в примере 1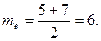

Пример 11. Найдем доверительный интервал для математического ожидания нормально распреде-ленной случайной величины, если объем выборки п = 49, 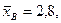σ = 1,4, а доверительная вероятность γ = 0,9.

Определим t, при котором Ф(t) = 0,9:2 = 0,45: t = 1,645. Тогда

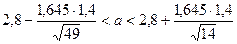, или 2,471 < a < 3,129. Найден доверительный интервал, в который попадает а с надежностью 0,9.

Пример 12. Пусть объем выборки п = 25, 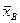= 3, s = 1,5. Найдем доверительный интервал для а при γ = 0,99.

Из таблицы находим, что t_γ (п = 25, γ = 0,99) = 2,797. Тогда 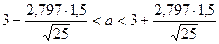, или 2,161< a < 3,839 – доверительный интервал, в который попадает а с вероятностью 0,99.

Пример 13. Пусть п = 20, s = 1,3. Найдем доверительный интервал для σ при заданной надежности γ = 0,95.

Из соответствующей таблицы находим q (n = 20, γ = 0,95 ) = 0,37. Следовательно, границы доверительного интервала: 1,3(1-0,37) = 0,819 и 1,3(1+0,37) = 1,781. Итак, 0,819 < σ < 1,781 с вероятностью 0,95.

Пример 14. Пусть проведено 50 независимых испытаний, и относительная частота появления события А оказалась равной 0,12. Проверим при уровне значимости α = 0,01 нулевую гипотезу Н₀: р = 0,1 при конкурирующей гипотезе Н₁: р > 0,1.

Найдем 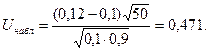Критическая область является правосторонней, а и_кр находим из равенства Ф(и_кр) = 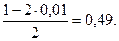Из таблицы значений функции Лапласа определяем и_кр = 2,33. Итак, U_набл < u_кр, и гипотеза о том, что р = 0,1, принимается.

Тексты задач для самостоятельного решения.

Задача №1.

Для изучения количественного признака X из генеральной совокупности извлечена выборка:

x_i 130 140 150 160 170 180 190

n_i 5 10 30 25 15 10 5,

(где x_i - выборочные варианты, а n_i - соответствующие частоты признака X)

Требуется:

1) Найти точечные оценки генеральной средней, генеральной дисперсии и генерального C.К.О.

2) Указать какие из найденных оценок являются смещенными, а какие - несмещенными.

3) Считая, что признак X распределен нормально, найти доверительный интервал для оценки его математического ожидания с надежностью g=0,95.

Задача №2.

Найти выборочные уравнения прямых линий регрессии признаков Y на X и X на Y по данной выборке:

(x,y)	(4;10)	(9;10)	(9;20)	(14;20)	(14;30)	(14;40)
nxy

(19;30)	(19;40)	(19;50)	(24;30)	(24;40)	(24;50)	(29;50)

Начертить график этих уравнений в одной системе координат. Сделать вывод о силе зависимости между X и Y.

Задача №3.

По выборкам объемов n=60 и m=50, извлеченным из нормальных генеральных совокупностей X и Y, дисперсии которых D(X)=96, D(Y)=120, найдены выборочные средние 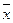=13,8 и 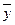=17,1.

Требуется при уровне значимости a=0,05 установить, значимо или незначимо различаются выборочные средние.

Ответы:

Задача №1:

1,2) 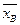=158,5 - несмещённая точечная статистическая оценка для

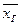
D_B=212,75 - смещённая точечная статистическая оценка для D_Г

s_в=14,59 - смещённая точечная статистическая оценка для s_г

3) 155,6<a<161,4 - доверительный интервал для a=M(X)

Задача №2:

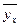=1,67x+1,6; 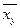=0,4y+5,45. Линейная зависимость между X и Y достаточно сильная, т.к. r_в=0,82 - близок к 1.

Задача №3:

Выборочные средние 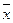=13,8 и 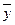=17,1 отличаются незначимо.